Рух часток речовини
Найбільш яскравим експериментальним підтвердженням представлень молекулярно-кінетичної теорії про безладний рух атомів і молекул є броунівський рух.



Рисунок 2.3а. Рисунок 2.3б.
У 1827 р. шотландський ботанік Р. Броун, вивчаючи рослини за допомогою мікроскопа, виявив дуже незвичайне явище. Плаваючі на воді спори (дрібне насіння деяких рослин) при спостереженні за ними в мікроскоп стрибкоподібно рухалися без видимих на те причин (див. рисунок 2.3а). Броун спостерігав цей рух декілька днів, проте так і не зміг дочекатися його припинення. Він його детально описав, але пояснити так і не зміг. Згодом це явище назвали броунівським рухом.
Пояснюється це явище таким чином. Молекули завжди знаходяться в постійному хаотичному русі. Вони безладно стикаються з іншими молекулами. Натрапляючи на спори, молекули викликають їх стрибкоподібні переміщення, що Броун і спостерігав в мікроскоп. А оскільки молекули в мікроскоп не видно, той рух спор здавався Броуну безпричинним.
На рисунку 2.3б зображена модель броунівського руху. Безліччю дрібних кульок позначені молекули води, а великою кулею - спора. Кількість ударів молекул об спору ліворуч і справа, згори і знизу, спереду і ззаду не завжди однаково. Під дією "переваги" ударів з якого-небудь одного боку спора перескакуватиме з місця на місце.

Рисунок 2.4.
В результаті швидкість броунівської частки безладно міняється по модулю і напряму, а її траєкторія є складною зигзагоподібною кривою (рис. 2.4). Теорія броунівського руху була створена. А Ейнштейном в1905 р. Експериментально теорія Ейнштейна була підтверджена в дослідах французького фізика ж. Перрена.
Дифузія
Самостійний рух часток речовини служить поясненням і ще одного фізичного явища. Розглянемо його на досліді.
У високу посудину з водою кинемо декілька крупинок марганцівки (рис 2.5). Вони опустяться на дно посудини, і навколо них незабаром утворюється фіолетова хмарка забарвленої води. Залишимо посудину в спокої на декілька годин. Спостерігаючи за нею весь цей час, ми виявимо поступове поширення забарвлення по усій висоті посудини. Говорять, що відбувається дифузія фарби у воду


Рисунок 2.5.
Дифузією називається взаємне проникнення речовин, що відбувається внаслідок безладного руху молекул речовини. Слово дифузія в перекладі з латинської мови означає розтікання, поширення.
Дифузія пояснюється таким чином. Частки речовин, безладно рухаючись, проникають в проміжки один між одним, що і означає змішування речовин. Найшвидше дифузія відбувається в газах. Повільніше - в рідинах, а в твердих тілах - зовсім повільно: роками. Відомий, наприклад, наступний дослід. Дві гладко відшліфовані пластини із золота і свинцю пролежали одна на одній близько 5 років. За цей час золото і свинець продифундували (проникли) один в одного на глибину близько 1 мм.
Дифузія має велике значення в житті людей і тварин. Так, наприклад, кисень з довкілля завдяки дифузії проникає всередину організму через шкіру людини. Поживні речовини завдяки дифузії проникають з кишечника в кров.
Завдання:
Налийте в склянку холодну воду і опустите в неї крупинку марганцівки. Не перемішуючи воду, визначите, через який час молекули марганцівки потраплять у верхній шар води. Поясните спостережуване явище.
Взаємне притягання і відштовхування молекул
Спостереження показують, що тверді тіла і рідини не розпадаються на окремі шматочки, не дивлячись на те, що молекули розділені проміжками і знаходяться в безперервному і безладному русі.
Виконаємо дослід. Візьмемо два свинцеві циліндри (рис. 2.6). Ножем або лезом зачистимо їх торці до блиску і щільно притиснемо один до одного. Ми виявимо, що циліндри "зчепляться". Сила їх зчеплення настільки велика, що при вдалому проведенні досліду циліндри витримують вагу гирі масою 5 кг (рис. 2. 7).



Рисунок 2.6. Рисунок 2.7. Рисунок 2. 8.
З досліду можна зробити висновок: частки речовин здатні притягуватися одна до одної. Проте це виникає лише тоді, коли поверхні тіл дуже гладкі (для цього і знадобилася зачистка лезом) і, крім того, щільно притиснуті одна до одної.
Частки будь-якої речовини здатні відштовхуватися один від одного. Це підтверджується тим, що рідкі, а особливо тверді тіла дуже важко стискувати. Наприклад, щоб здавити гумову гумку, потрібно значну силу! Гумку набагато легше зігнути, ніж здавити (рис. 2.8).
Притягання або відштовхування часток речовин виникає лише у тому випадку, коли вони знаходяться в безпосередній близькості. На відстанях, трохи більших розмірів самих часток, вони притягуються. На відстанях, менших розмірів часток, вони відштовхуються. Якщо ж поверхні тіл віддалені на відстань, помітно більшу, ніж розмір часток, то взаємодія між ними не проявляється ніяк. Наприклад, не можна помітити ніякого притягання між свинцевими циліндрами, якщо їх спочатку не стискувати, тобто не зблизити їх частки.
Виникнення сили пружності. Стискуючи або розтягуючи, згинаючи або скручуючи тіло, ми зближуємо або віддаляємо його молекули. Тому між ними виникають сили притягання-відштовхування, які ми і об'єднуємо терміном "сила пружності".


Рисунок 2.9.
На рисунку 2.9 умовно зображені частки гуми ластику, що згинається. Ви бачите, що біля верхньої грані ластику молекули гуми зближуються одна з одною. Це призводить до виникнення між ними сил відштовхування. Поблизу нижньої грані гумки частки віддаляються один від одного, що призводить до виникнення між ними сил притягання. В результаті їх дії гумка прагне випрямитися, тобто повернутися в недеформований стан. Іншими словами, в гумці виникає сила пружності, спрямована протилежно силі, що викликала деформацію.
Швидкість руху часток і температура
Такі явища, як, наприклад, нагрівання і охолодження повітря, танення льоду, плавлення металів, кипіння води, називається тепловими явищами.
Відомо, що при нагріванні вода стає спочатку теплою, а потім гарячою. Нагріта піч поступово охолоджується, а повітря в кімнаті нагрівається. Словами "холодний", "теплий", "гарячий" ми називаємо тепловий стан тіл. Однією з величин, що характеризують тепловий стан тіл, являється температура.
Якщо спостерігати дифузію рідин в двох посудинах, то можна виявити, що при вищій температурі дифузія проходить швидше. Це означає, що швидкість руху молекул і температура пов'язані між собою.
Чим більша швидкість руху молекул тіла, тим вища його температура.
Тепла вода складається з таких же молекул, що і холодна. Різниця в тому, що молекули теплої води рухаються швидше, ніж молекули холодної води. Але ж чим більше швидкість тіла, тим більше його кінетична енергія.
Молекули мають надзвичайно малі розміри. Прості одноатомні молекули мають розмір порядку 10-10м. Але, якщо узяти 20 г води, там буде приблизно 6·1023 молекул, і кожна молекула рухається, отже, має кінетичну енергію.
Безладний хаотичний рух молекул називається тепловим рухом. Кінетична енергія теплового руху росте із зростанням температури.
Отже, при будь-якій температурі спостерігається самостійний рух часток усіх речовин - твердих, рідких і газоподібних. Оскільки частки рухаються, вони мають кінетичну енергію. Ця енергія тим більше, чим вище температура тіла.
Питання:
1. Які теплові явища ви знаєте?
2. Чим відрізняється рух молекул холодної води від руху молекул гарячої води?
3. Чому, опускаючи руку у воду, ви відразу відчуваєте холодна вона або гаряча?
4. Чому тверді тіла і рідини не розпадаються самі собою на окремі молекули?
5. Які явища вказують, що молекули не лише притягуються, але і відштовхуються одна від одної?
Завдання:
Налийте в дві склянки однакову кількість води. Одну з них поставте в тепле місце, а іншу в холодне. Через деякий час опустите в кожну склянку крупинку марганцівки. Поставте склянки на колишні місця. Через певний час відмічайте положення межі забарвленої і чистої води. Поясните спостережуване явище.
Три стани речовини
На прикладі води, ртуті і інших тіл ми бачимо, що речовини в природі можуть знаходитися в трьох станах: у вигляді твердого тіла, рідини і газу. Ці стани називаються агрегатними станами. Властивості тіл в різних станах різні.
Тверде тіло в звичайних умовах важко стиснути або розтягнути, воно зберігає свій об'єм.
Збереження об'єму і форми - властивість твердих тіл.
Рідина легко міняє свою форму, вона набуває форми посудини, в яку її наливають.
Форму рідини змінити легко, але об'єм її змінити важко.
Рідини зберігають об'єм, але легко міняють свою форму.
Багато газів прозорі і безбарвні, тому ми їх не бачимо. Ми не бачимо повітря, але при швидкому пересуванні ми його можемо відчувати.
Газ може бути сильно стислий. Гази в тисячі разів більше стискувані, ніж рідини.
Гази мають ще одну властивість, якої немає в рідинах і твердих тілах, а саме вони заповнюють увесь наданий об'єм.
Гази не мають постійного об'єму і власної форми.
Спеціальними дослідженнями встановлено, що молекули речовини не змінюються при зміні його агрегатного стану. Наприклад, на рисунку 2.10 показано розташування молекул однієї і тієї ж речовини - води в трьох агрегатних станах. Пар (рис 2.10а), вода (рис 2.10б) і лід (рис 2.10в). Молекули пари, води і льоду не відрізняються одна від одної. Отже, ці три стани речовини розрізняються не молекулами, а тим, як молекули розташовані і як рухаються.
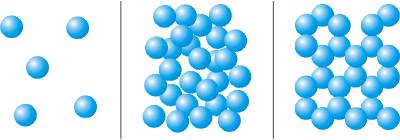
а б в
Рисунок 2.10.
У газах відстань між молекулами на багато більша розмірів самих молекул. На таких відстанях між молекулами практично немає сили притягання. Тому гази не мають власної форми і постійного об'єму.
Властивості рідин пояснюються тим, що проміжки між молекулами малі: молекули в рідинах упаковані так щільно, що відстань між кожними двома молекулами менша розмірів молекули. На таких відстанях притягання молекул одна до одної вже значне. Проте воно не стільки велике, щоб рідина зберігала свою форму.
Тверді тіла в звичайних умовах зберігають свою форму. Це пояснюється тим, що відстань між молекулами ще менша, ніж у рідин.
У наступних параграфах ми більш детально розглянемо будову твердих, рідких і газоподібних речовин з точки зору МКТ.
§ 17. Кристалічні і аморфні тіла
Якщо помістити шматок пластиліну і шматок льоду в тепле місце, то через деякий час частина льоду розплавиться (стане рідиною), а частина - залишиться у вигляді твердого шматочка. Пластилін за той же час лише трохи розм'якшиться. Ще через деякий час увесь лід розплавиться, а пластилін - поступово "роз'їдеться" по поверхні столу, все більш і більш розм'якшуючись.
Отже, існують тіла, які при плавленні не розм'якшуються, а з твердого стану перетворюються відразу на рідину. Під час плавлення таких тіл завжди можна відокремити рідину від частини тіла, яка ще не розплавилася. Ці тіла - кристалічні. Існують також тверді тіла, які при нагріванні поступово розм'якшуються, стають усе більш текучими. Для таких тіл неможливо вказати температуру, при якій вони перетворюються на рідину (плавляться). Ці тіла називають аморфними.
Кристалічні тіла можуть бути монокристалами і полікристалами. Полікристалічні тіла складаються з багатьох зрощених між собою хаотично орієнтованих маленьких кристалів, які називаються кристалітами.


Рисунок 2.11.
На рисунку 2.11 ви бачите збільшену фотографію поверхні відшліфованої алюмінієвої пластини. Чорні лінії на ній - проміжки між окремими кристалами алюмінію. Полікристалічне тіло утворюється в результаті того, що одночасно починають утворюватися відразу безліч кристалів. Так відбувається, наприклад, при застиганні розплавленого олова, цинку і, взагалі, усіх металів. Отже, усі метали мають кристалічну або, точніше, полікристалічну будову.
Великі монокристали рідко зустрічаються в природі. Найчастіше кристалічні тверді тіла, у тому числі і ті, які виготовляють штучно, являються полікристалами.
Теоретично доведено, що усього може існувати 230 різних просторових кристалічних структур. Більшість з них (але не всі) виявлені в природі або створені штучно.
Кристалічні грати металів часто мають форму шестигранної призми (цинк, магній), гранецентрованого куба (мідь, золото) або об'ємноцентрованого куба (залізо).
Структури кристалічних грат експериментально вивчаються за допомогою дифракції рентгенівського випромінювання на монокристалах або полікристалічних зразках, або за допомогою електронного мікроскопа.
На рисунку 2.12 наведені приклади простих кристалічних грат. Слід пам'ятати, що частки в кристалах щільно упаковані, так що відстань між їх центрами приблизно рівна розміру часток. У зображенні кристалічних грат вказується тільки положення центрів часток.
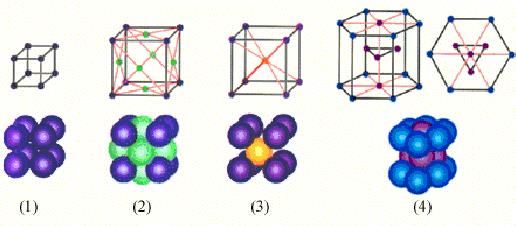
Рисунок 2.12.
Прості кристалічні грати: 1 - прості кубічні грати; 2 - гранецентровані кубічні грати; 3 - об’ємноцентровані кубічні грати; 4 - гексагональні грати.
У простих кубічних гратах частки розташовуються у вершинах куба. У гранецентрованих гратах частки розташовуються не лише у вершинах куба, але і в центрах кожної його грані. У об'ємноцентрованих кубічних гратах додаткова частка розташовується в центрі кожного елементарного кубічного осередку.
Рух часток кристалів. У молекулярно-кінетичній теорії вважається, що частки кристалічних твердих тіл безперервно коливаються біля положень рівноваги. Розмах коливань часток невеликий в порівнянні з розмірами самих часток, тому на фотографіях їх відхилення непомітні. У моделі "кристалічна грата" положення рівноваги часток відмічені вузлами.
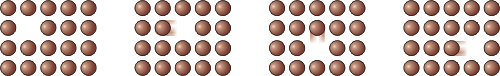
Рисунок 2.13.
Коливальний рух часток кристалів - основний їх рух. Проте частки можуть іноді перескакувати з місця на місце. Цьому сприяє той факт, що в кристалах є дефекти. Наприклад, в порожнє місце в ряду - "дірку" - може перескочити частка з сусіднього ряду (рисунок 2.13). В результаті утворюється нова "дірка". У неї може перескочити частка іншого ряду і так далі. Саме завдяки дефектам кристалічної будови тверді тіла здатні дифундувати один в одного.
Будова аморфних тіл. Дослідження за допомогою електронного мікроскопа, а також за допомогою рентгенівських променів свідчать, що в аморфних тілах не спостерігається строгого порядку в розташуванні їх часток. На рисунку 2.14 зображено розташування часток в кристалічному кварці, а на рисунку 2.15 - в аморфному. Ці речовини складаються з одних і тих же часток - молекул оксиду кремнію SiO2.
Кристалічний стан кварцу виходить, якщо розплавлений кварц охолоджувати повільно. Якщо ж охолодження розплаву буде швидким, то молекули не встигнуть "вишикуватися" в стрункі лави, і вийде аморфний кварц.
Частки аморфних тіл безперервно і безладно коливаються. Вони частіше, ніж частки кристалів можуть перескакувати з місця на місце. Цьому сприяє і те, що частки аморфних тіл розташовані неоднаково щільно: між ними є порожнечі.
 |  |
Рисунок 2.14. Рисунок 2.15.
Характерною особливістю аморфних тіл є їх ізотропність, тобто незалежність усіх фізичних властивостей (механічних, оптичних і так далі) від напряму. По своїй структурі аморфні тіла дуже близькі до рідин. Прикладами аморфних тіл можуть служити скло, різні затверділі смоли (бурштин), пластики і т. д. Якщо аморфне тіло нагрівати, то воно поступово розм'якшується, і перехід в рідкий стан займає значний інтервал температур.
Кристалізація аморфних тіл.
З часом деякі аморфні речовини мимоволі переходять в кристалічний стан. Наприклад, цукрові льодяники або свіжий мед, полишені в теплому місці, через декілька місяців стають непрозорими. Говорять, що мед і льодяники "зацукрувалися". Розламавши льодяник або зачерпнувши мед ложкою, ми дійсно побачимо кристали цукру. Самовільна кристалізація аморфних тіл свідчить, що кристалічний стан речовини є стійкішим, ніж аморфне. МКТ пояснює це так. Міжмолекулярні сили притягання-відштовхування примушують частки аморфного тіла перескакувати переважно туди, де є порожнечі. В результаті виникає більш впорядковане, ніж раніше розташування часток, тобто утворюється полікристал.
§ 18. Будова рідин
Припустимо, що перед вами знаходиться баночка з невідомою прозорою речовиною. Як дізнатися, що в ній знаходиться: рідина або тверде тіло? Дуже просто: потрібно узяти баночку в руки і нахилити. Якщо речовина почне текти, значить, це рідина.
Отже, відмітною ознакою рідини є текучість - здатність змінювати форму за малий час під дією навіть малої сили. Завдяки цій властивості усі рідини ллються у вигляді струменів, розбризкуються краплями, набувають форми тієї посудини, в яку їх наллють.
 |  |
Рисунок 2.16. Рисунок 2.17.
Здатність змінювати форму у різних рідин виражена по-різному. На рисунку 2.16 в лівій склянці знаходиться вода, а в правому мед. Під дією однієї і тієї ж сили (сили тяжіння) меду потрібно більше часу, щоб змінити свою форму, ніж воді.
Говорять, що ці речовини мають неоднакову в'язкість: у меду вона більша, ніж у води.
Проте, змінюючи форму, рідина не змінює свого об'єму. Погляньте на рисунок 2.17. Вода, що знаходилася в мензурці, мала форму циліндра і об'єм 300 мл. Після переливання в чашу рідина набула конусоподібної форми, але зберегла колишній об'єм 300 мл. Властивість рідини зберігати об'єм інакше називають пружністю рідини.
Ще однією загальною властивістю усіх рідин є їх здатність передавати на всі боки чинений на них тиск (закон Паскаля). Менш в'язкі рідини роблять це швидко, а в'язкі - довго. Тиск, який передається на спирт або воду, швидко пошириться навіть на велику відстань. А тиск, який передається на густе масло або мед, поширюватиметься набагато повільніше.
Будова рідин.У молекулярно-кінетичній теорії вважається, що в рідинах, як і в аморфних тілах, немає строгого порядку в розташуванні молекул; у різних частинах тіла вони розташовані неоднаково щільно. Тому міжмолекулярні проміжки мають різні розміри, у тому числі і такі, що туди може поміститися ще одна молекула. Це дозволяє часткам перескакувати в довколишні "дірки". Такі перескоки молекул в рідинах відбуваються дуже часто: декілька мільярдів разів в секунду.
Якщо на рідину подіє яка-небудь зовнішня сила, наприклад, сила тяжіння, перескоки часток відбуватимуться, в основному, у напрямі її дії (тобто вниз). Це приведе до того, що рідина набуде форми краплі, що витягується, або струменя (рис 2.18), що ллється. Отже, текучість рідин пояснюється частими перескоками молекул з одного стійкого положення в інше. У в'язких рідинах, наприклад, меді, перескоки молекул з одного стійкого положення в інше відбуваються значно рідше, ніж, наприклад, у воді або спирті. Тому під дією зовнішньої сили в'язка рідина повільніше змінюватиме свою форму; на це їй буде потрібно більше часу. Проте, будь-які перескоки часток (часті або рідкісні) обумовлюють передачу рідинами тиску у всіх напрямках (закон Паскаля).
Перескоки молекул рідин відбуваються часто, проте приблизно в 100 разів частіше молекули здійснюють коливання в місці свого останнього перескоку. В цей час вони безперервно ударяються одна з одною, тому навіть мале стискування рідини призводить до різкої протидії зі сторони рідини.


Рисунок 2.18. Рисунок 2.19.
Приклад ближнього порядку молекул рідини і дальнього порядку молекул кристалічної речовини : 1 - вода; 2 - лід.
Це означає різке підвищення тиску рідини на стінки посудини, в якій її стискують. Іншими словами, рідина чинитиме сильний опір стискуванню. Цим і пояснюється пружність рідини. У рідинах молекули мають значно більшу свободу для теплового руху. Вони не прив'язані до певних центрів і можуть переміщатися по усьому об’єму рідини. Цим пояснюється текучість рідин. Близько розташовані молекули рідини також можуть утворювати впорядковані структури з декількох молекул. Це явище називається ближнім порядком на відміну від дальнього порядку, характерного для кристалічних тіл (рис 2.19).
Питання.
1. У чому відмінність моно- і полікристалів?
2. Опишіть будову монокристала.
3. Які бувають дефекти кристалів?
4. Що таке кристалічна гратка?
5. Охарактеризуйте рух часток в кристалах.
6. Як виявити відмінність між кристалічними і аморфними тілами.
7. Охарактеризуйте будову аморфних тіл.
8. Про що свідчить самовільна кристалізація аморфних тіл?
9. Чому ми говоримо, що вода і мед мають різну в'язкість?
10. Опишіть мікроскопічну будову рідин.
11. Охарактеризуйте рух часток рідини.
12. Як МКТ пояснює пружність рідини?
§ 19. Газоподібні тіла
У природі існує величезна кількість газів: водень, кисень, вуглекислий газ, водяна пара, пари ртуті, азот, озон, хлор і так далі. Усі вони дуже різні. Водень легкий, а вуглекислий газ - важкий; азот не пахне, а озон - "щипає" ніс; водяні пари нешкідливі, а пари ртуті - отруйні; повітря безбарвне, а хлор має жовто-зелений колір. Проте усі без виключення гази мають одну загальну властивість: вони легко стискуються.
 |  |
Рисунок 2.20а. Рисунок 2.20б.
На відміну від рідин і твердих тіл, гази можна стискувати дуже сильно: в 100 і більше разів. Чому ж це можливо?
Будова газоподібних тіл.В молекулярно-кінетичній теорії встановлено, що при тисках газу, близьких до атмосферного, відстані між молекулами газу у багато разів більші розмірів самих часток. Це схематично показано на рисунку 2.20а. Але якщо газ стискувати, тобто збільшити його тиск, то міжмолекулярні проміжки зменшуються. Це показано на рисунку 2.20б.
Згадаємо, що в газах дифузія протікає набагато швидше, ніж в рідких і твердих тілах. Значить, молекули газів вільно переміщаються в просторі. Це може бути лише у тому випадку, якщо кінетична енергія руху часток газу значно більша потенціальної енергії їх притягання одна до одної. Перевага кінетичної енергії молекул газу над їх потенціальною енергією якраз і означає, що молекули газу практично вільно літають на всіх напрямках. Тому, наприклад, неможливо заповнити газом половину посудини: літаючи у всіляких напрямах, молекули незабаром рівномірно розподіляться по усьому об’єму посудини.
 Тиск газу.На рисунку 2.21 зображено дві посудини: ліва - з рідиною, а права - з газом. Кожна посудина забезпечена трьома манометрами: поблизу дна, в середній частині посудини і поблизу горловини. Усі манометри посудини з газом показують однакові тиски, а манометри посудини з рідиною - зростаючі значення у міру просування від горловини до дна. Чому?
Тиск газу.На рисунку 2.21 зображено дві посудини: ліва - з рідиною, а права - з газом. Кожна посудина забезпечена трьома манометрами: поблизу дна, в середній частині посудини і поблизу горловини. Усі манометри посудини з газом показують однакові тиски, а манометри посудини з рідиною - зростаючі значення у міру просування від горловини до дна. Чому?
 |  |
Рисунок 2.21. Рисунок 2.22.
Рідина давить на дно і стінки посудини тому, що на неї діє сила тяжіння. Частки рідини, притягуючись до Землі, придавлюють одна одну. Здійснюючи коливання, частки "бомбардують" дно і стінки посудини. Образно виражаючись, таке "підневільне бомбардування" і є тиск рідини. Саме тому тиск рідини зростає у міру опускання до дна посудини.
Тиск, що створюється газом, має принципово інше походження. На молекули газу теж діє сила тяжіння, проте вони не придавлюють одна одну, оскільки вільно літають у всіх напрямках усередині посудини. Частки постійно ударяються одна з одною і із стінками посудини. Образно кажучи, тиск газу - це вже "волелюбне бомбардування" (рис 2.22).
Встановлено, що при збільшенні температури тиск газу зростає. Молекулярно-кінетична теорія пояснює цей факт так. Підвищення температури призводить до збільшення швидкості руху часток газу. Тому "бомбардування" частками стінок посудини посилюється, що і означає зростання тиску газу. Подібно до рідин, гази теж передають на всі боки чинений на них тиск (закон Паскаля).
Рисунок 2.23 ілюструє відмінність газоподібної речовини від рідини на прикладі води. Молекула води H2O складається з одного атома кисню і двох атомів водню, розташованих під кутом 104°. Середня відстань між молекулами пари в десятки разів перевищує середню відстань між молекулами води.
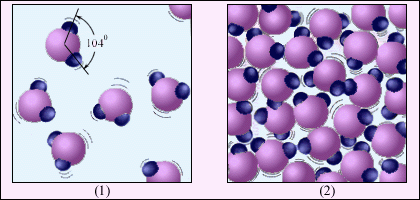
Рисунок 2. 23.
Водяна пара (1) і вода (2). Молекули води збільшені приблизно в 5·107 разів.
У газах відстані між молекулами значно більша їх розмірів. Сили взаємодії між молекулами на таких великих відстанях малі, і кожна молекула рухається уздовж прямої лінії до чергового зіткнення з іншою молекулою або із стінкою посудини (рис 2.22) Середня відстань між молекулами повітря за нормальних умов порядку 10-8м, тобто в десятки разів перевищує розмір молекул. Слабку взаємодію між молекулами пояснює здатність газів розширюватися і заповнювати увесь об'єм посудини. У межі, коли взаємодія прагне до нуля, ми приходимо до уявлення про ідеальний газ.
Питання:
1. Як МКТ пояснює хорошу стисливість газів?
2. Охарактеризуй мікроскопічну будову газів.
3. У чому відмінність тисків, що створюються рідиною і газом?
4. Як МКТ пояснює збільшення тиску газу при підвищенні його температури?
Тема 6
Основні положення молекулярно-кінетичної теорії ідеального газу
§ 20. Ідеальний газ і його параметри
Простою моделлю молекулярно-кінетичної теорії є модель ідеального газу. У кінетичній моделі ідеального газу молекули розглядаються як ідеально пружні кульки, що взаємодіють між собою і із стінками посудини. Потенціальна енергія взаємодії між молекулами не враховується. Сумарний об'єм усіх молекул передбачається малим в порівнянні з об'ємом посудини, в якому знаходиться газ. Модель ідеального газу досить добре описує поведінку реальних газів в широкому діапазоні тисків і температур.
Параметрами ідеального газу називають фізичні величини, за допомогою яких можна описати стан газу. Параметри діляться на мікроскопічні (маса, швидкість, кінетична енергія молекул) і макроскопічними параметрами (тиск, об'єм, температура).
Параметри ідеального газу :
р -тиск. (вимірюється в паскалях Па).
V- об'єм. ( вимірюється в м3).
Т -температура (вимірюється в градусах за шкалою Кельвіна (К) 0°С = 273К).
У молекулярно-кінетичній теорії вводиться поняття кількості речовини. Одиницею кількості речовини є 1 моль.
Моль - це кількість речовини, що містить стільки ж часток (молекул), скільки міститься атомів в 0,012 кг вуглецю 12C. Молекула вуглецю складається з одного атома.
Таким чином, в одному молі будь-якої речовини міститься одне і те ж число часток (молекул). Це число називається сталою Авогадро NA :
NA = 6,02·1023 моль-1.
Стала Авогадро - одна з найважливіших сталих в молекулярно-кінетичній теорії.
Кількість речовини ν (грецька буква ню) визначається як відношення числа N молекул речовини, до числа Авогадро NA:
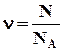 . (2.1)
. (2.1)
Масу одного моля речовини називають молярною масою M. Молярна маса дорівнює добутку маси m0 однієї молекули цієї речовини на сталу Авогадро :
M = NA·m0.
Молярна маса виражається в кілограмах на моль (кг/моль). Для речовин, молекули яких складаються з одного атома, часто використовується термін атомна маса.
За одиницю маси атомів і молекул приймається 1/12 маси атома ізотопу вуглецю 12C (з масовим числом 12). Вона називається атомною одиницею маси (а. е. м):
1 а.е.м. =1,66·10-27 кг
§ 21. Рівняння стану ідеального газу
Стан деякої маси ідеального газу визначається значеннями трьох параметрів : тиску р, об'єму V і температури T. Ці параметри закономірно пов'язані один з одним, таким чином, що зміна одного їх призводить до зміни інших.
Співвідношення, що дають зв'язок між параметрами будь-якого тіла, називається рівнянням стану цього тіла.
Рівняння, що встановлює зв'язок між тиском, об'ємом і температурою ідеального газу було отримано в середині XIX століття французьким фізиком Б. Клапейроном.
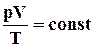 . (2.2)
. (2.2)
Відповідно до закону, встановленого Авогадро, коли кількість речовини газу ν дорівнює 1 моль:
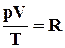 . (2.3
. (2.3
Величина R називається універсальною газовою сталою. Її чисельне значення в СІ становить:
R = 8,31 Дж/моль·К.
Для довільної маси газу рівняння Клапейрона можна записати у виді:
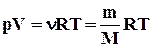 . (2.4)
. (2.4)
У формі (2.4) воно було уперше записане Д. Менделєєвим. Тому рівняння стану газу називається рівнянням Клапейрона-Менделєєва.
Якщо температура газу становить Tн=273,15 К (0°С), а тиск рн = 1 атм = 1,013·105 Па, то говорять, що газ знаходиться за нормальних умов. Як випливає з рівняння стану ідеального газу, один моль будь-якого газу за нормальних умов займає один і той же об'єм V0, рівний
V0 = 0,0224 м3/моль = 22,4 дм3/моль.
Для суміші не взаємодіючих газів рівняння стану набирає вигляду
pV= (ν1 + ν2 + ν3 + ..)·RT. (2.5)
де ν1, ν2, ν3 і т. д. - кількість речовини кожного з газів в суміші.
§ 22. Газові процеси
Слід зазначити, що задовго до того, як рівняння стану ідеального газу було теоретично отримане на основі молекулярно-кінетичної моделі, закономірності поведінки газів в різних умовах були добре вивчені експериментально. Тому рівняння Клапейрона - Менделєєва можна розглядати, як узагальнення дослідних фактів, які знаходять пояснення в молекулярно-кінетичній теорії.
Газ може брати участь в різних теплових процесах, при яких можуть змінюватися усі параметри, що описують його стан (p, V і T). Якщо процес протікає досить повільно, то у будь-який момент система близька до свого рівноважного стану. Такі процеси називаються квазістатичними. У звичному для нас масштабі часу ці процеси можуть протікати і не дуже повільно. Наприклад, розрідження і стискування газу в звуковій хвилі відбуваються сотні разів в секунду, але цей процес можна розглядати як квазістатичний. Квазістатичні процеси можуть бути зображені на діаграмі станів (наприклад, в координатах p, V) у вигляді деякої лінії, кожна точка якої представляє рівноважний стан.
Інтерес представляють процеси, в яких один з параметрів (p, V або T) залишається незмінним. Такі процеси називаються ізопроцесами.
Ізотермічний процес (T = const)
Ізотермічним процесом називають процес, що протікає при постійній температурі T. З рівняння стану ідеального газу виходить, що при постійній температурі T і незмінній кількості речовини в посудині добуток тиску p газу на його об'єм V повинен залишатися постійним:
рV = const. (2.6)
Графічно (в координатах p, V) ізотермічні процеси зображають сімейством гіпербол p ~ 1/V, які називаються ізотермами. Оскільки коефіцієнт пропорційності в цьому співвідношенні збільшується із зростанням температури, ізотерми, що відповідають вищим значенням температури, розташовуються на графіці вище за ізотерми, що відповідають меншим значенням температури (рис. 2.24). Рівняння ізотермічного процесу було отримане експериментально англійським фізиком Р. Бойлем (1662 р.) і незалежно французьким фізиком Е. Маріоттом (1676 р.). Тому це рівняння називають законом Бойля-Маріотта.
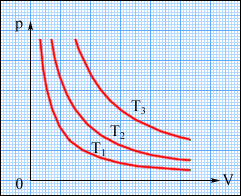
Рисунок 2.24.
Сімейство ізотерм на площині (p, V). T3 > T2 > T1.
Ізохорний процес (V = const)
Ізохорний процес - це процес нагрівання або охолодження газу при постійному об'ємі V і за умови, що кількість речовини в посудині залишається незмінною.
Як випливає з рівняння стану ідеального газу, за цих умов тиск газу pзмінюється прямо пропорціональний його абсолютній температурі: p ~ T або
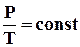 . (2.7)
. (2.7)
На площині (p, T) ізохорні процеси для заданої кількості речовини при різних значеннях об'єму V зображуються сімейством прямих ліній, які називаються ізохорами. Більшим значенням об'єму відповідають ізохори з меншим нахилом по відношенню до осі температур (рис.2.25).
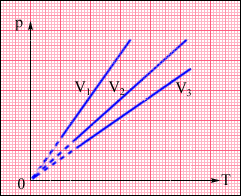
Рисунок 2.25.
Сімейство ізохор на площині (p, T). V3 > V2 > V1.
Експериментально залежність тиску газу від температури досліджував французький фізик Ж. Шарль (1787 р.). Тому рівняння ізохорного процесу називається законом Шарля.
Рівняння ізохорного процесу може бути записане у виді:
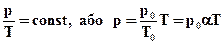 . (2.8)
. (2.8)
де p0 - тиск газу при T = T0 = 273,15 К (0°С). Коефіцієнтα, рівний (1/273,15) К-1, називають температурним коефіцієнтом тиску.
Ізобарний процес (p = const)
Ізобарним процесом називають процес, що протікає при незмінному тиску p.
Рівняння ізобарного процесу для деякої незмінної кількості речовини має вигляд:
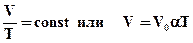 . (2.9)
. (2.9)
де V0 - об'єм газу при температурі 0°С. Коефіцієнт α рівний (1/273,15) К-1. Його називають температурним коефіцієнтом об'ємного розширення газів.
На площині (V, T) ізобарні процеси при різних значеннях тиску p зображуються сімейством прямих ліній (рис. 2.26), які називаються ізобарами.
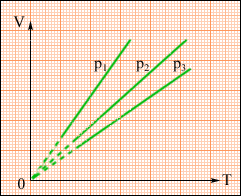
Рисунок. 2.26.
Сімейство ізобар на площині (V, T). p3 > p2 > p1.
Залежність об'єму газу від температури при незмінному тиску була експериментально досліджена французьким фізиком Ж. Гей-Люссаком. (1862 р.). Тому рівняння ізобарного процесу називають законом Гей-Люссака.
Експериментально встановлені закони Бойля-Маріотта, Шарля і Гей-Люссака знаходять пояснення в молекулярно-кінетичній теорії газів.
Приклади розв’язку завдань :
1. Об'єм газу під тиском 6,4·105Па і температурі 288 К дорівнює 0,6 м3. При якій температурі та ж маса газу займе об'єм 1,6м3, якщо тиск стане рівним 2,25·105Па?
Дано:

 P1=6,4·105 Па. Оскільки маса газу не змінилася,
P1=6,4·105 Па. Оскільки маса газу не змінилася,
T1=288 K можна записати . З цього рівняння
 V1= 0,6 м3
V1= 0,6 м3
P2=2,25·105 Па. .
V2= 1,6 м3
 Т2- ? Т2=2,25·105 ·1,6·288/6,4·105·0,6= 270К Ответ:Т2=270К.
Т2- ? Т2=2,25·105 ·1,6·288/6,4·105·0,6= 270К Ответ:Т2=270К.
1. Балон об’ємом 0,1 м3 містить 6 кг кисню. При якій температурі виникає небезпека вибуху, якщо балон витримує тиск 5·106 Па. Молярна маса кисню 3,2·10-2 кг/моль.
Дано:
 P=5·106 Па Запишемо рівняння стану ідеального газу
P=5·106 Па Запишемо рівняння стану ідеального газу
V=0,1 м3 PV=νRT.
m= 6кг. Кількість молей представимо
М=3,2·10-2 кг/моль ν=m/M = 6кг/0,032кг/моль = 187,5 моль.
 Т- ? Тоді Т=PV/νR =5·106 Па·0,1м3/187,5моль·8,31Дж/моль·К≈320 К.
Т- ? Тоді Т=PV/νR =5·106 Па·0,1м3/187,5моль·8,31Дж/моль·К≈320 К.
Відповідь: небезпека вибуху виникає при температурі 320К.
§ 23. Основне рівняння МКТ газів
Завдання молекулярно-кінетичної теорії полягає в тому, щоб встановити зв'язок між мікроскопічними (маса, швидкість, кінетична енергія молекул) і макроскопічними параметрами (тиск, об'єм, температура) ідеального газу.
В результаті кожного зіткнення швидкості молекул можуть змінюватися по модулю і по напряму; на інтервалах між послідовними зіткненнями молекули рухаються рівномірно і прямолінійно. У моделі ідеального газу передбачається, що усі зіткнення відбуваються за законами пружного удару, тобто підпорядковуються законам механіки.
Використовуючи модель ідеального газу, визначимо тиск газу на стінку посудини.
Взаємодію молекули із стінкою розглядаємо, як абсолютно пружний удар. В результаті проекція vx швидкості молекули, перпендикулярна стінці, змінює свій знак на протилежний, а проекція vy швидкості, паралельна стінці, залишається незмінною (рис.2.27). Тому зміна імпульсу молекули дорівнюватиме 2m0vx, де m0 - маса молекули.
Виділимо на стінці деякий майданчик S (рис. 2.28). За час Δt з цим майданчиком зіткнуться усі молекули, що мають проекцію швидкості vx, спрямовану у бік стінки, і знаходяться в циліндрі з площею основи S, і висотою vxΔt.
 |  |
Рисунок 2.27. Рисунок 2.28.
Нехай в одиниці об'єму посудини містяться n молекул; тоді число молекул в об'ємі циліндра становить nSvxΔt. Але з цього числа лише половина рухається у бік стінки, а інша половина рухається в протилежному напрямі і із стінкою не стикається. Отже, число ударів молекул об майданчик S за час Δt дорівнює:

 Оскільки кожна молекула при зіткненні із стінкою змінює свій імпульс на величину 2m0vx, то повна зміна імпульсу усіх молекул, що зіткнулися за час Δtз майданчиком S, рівна:
Оскільки кожна молекула при зіткненні із стінкою змінює свій імпульс на величину 2m0vx, то повна зміна імпульсу усіх молекул, що зіткнулися за час Δtз майданчиком S, рівна:
За законами механіки ця зміна імпульсу усіх молекул, що зіткнулися із стінкою, відбувається під дією імпульсу сили FΔt, де F - деяка середня сила, діюча на молекули з боку стінки на майданчику S. Але за 3-м законом Ньютона така ж по модулю сила діє з боку молекул на майданчик S. Тому можна записати:

Розділивши обидві частини на SΔt, отримаємо:

де Р - тиск газу на стінку посудини.
При виводі цього співвідношення передбачалося, що усі n молекул, які знаходяться в одиниці об'єму газу, мають однакові проекції швидкостей на вісь X. Насправді це не так.
 Щоб уточнити формулу для тиску газу на стінку посудини, припустимо, що усі молекули розбиті на групи, n1, n2, n3 і т. д. з проекціями швидкостей vx1, vx2, vx3 і т. д. відповідно.
Щоб уточнити формулу для тиску газу на стінку посудини, припустимо, що усі молекули розбиті на групи, n1, n2, n3 і т. д. з проекціями швидкостей vx1, vx2, vx3 і т. д. відповідно.
 При цьому:
При цьому:
Кожна група молекул вносить свій вклад в тиск газу. В результаті зіткнень із стінкою молекул з різними значеннями проекцій vxi швидкостей виникає сумарний тиск

Сума, що входить в цей вираз, - це сума квадратів проекцій vx усіх n молекул в одиничному об'ємі газу. Якщо цю суму розділити на n, то ми отримаємо
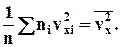
Тепер формулу для тиску газу можна записати у виді

Оскільки усі напрями для векторів швидкостей молекул рівно ймовірні, середнє значення квадратів їх проекцій на координатні осі рівні між собою:
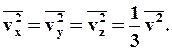
 Остання рівність витікає з формули:
Остання рівність витікає з формули:
Формула для середнього тиску газу на стінку посудини запишеться у виді

(2.10)
 Це рівняння встановлює зв'язок між тиском p ідеального газу, масою молекули m0, концентрацією молекул n, середнім значенням квадрата швидкості і середньою кінетичною енергією Ek поступального руху молекул. Його називають основним рівнянням молекулярно-кінетичної теорії газів.
Це рівняння встановлює зв'язок між тиском p ідеального газу, масою молекули m0, концентрацією молекул n, середнім значенням квадрата швидкості і середньою кінетичною енергією Ek поступального руху молекул. Його називають основним рівнянням молекулярно-кінетичної теорії газів.
Таким чином, тиск газу дорівнює двом третинам середньої кінетичної енергії поступальної ходи молекул, що містяться в одиниці об'єму.
Температура
У основне рівняння молекулярно-кінетичної теорії газів (2.10) входить добуток концентрації молекул n на середню кінетичну енергію Ek поступального руху молекул. Якщо припустити, що газ знаходиться в посудині незмінного об'єму V, то 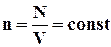 (N - число молекул в посудині). В цьому випадку зміна тиску Δp пропорційна зміні ΔEk середньої кінетичної енергії.
(N - число молекул в посудині). В цьому випадку зміна тиску Δp пропорційна зміні ΔEk середньої кінетичної енергії.
Виникають питання, яким чином можна на досліді змінювати середню кінетичну енергію руху молекул в посудині незмінного об'єму? Яку фізичну величину треба змінити, щоб змінилася середня кінетична енергія. Такою величиною у фізиці є температура.
Поняття температури тісно пов'язане з поняттям теплової рівноваги. Тіла, що знаходяться в контакті одне з одним, можуть обмінюватися енергією. Енергія, що передається одним тілом іншому при тепловому контакті, називається кількістю теплоти.
Теплова рівновага - це такий стан системи тіл, що знаходяться в тепловому контакті, при якому не відбувається теплопередачі від одного тіла до іншого, і усі макроскопічні параметри тіл залишаються незмінними. Температура - це фізичний параметр, однаковий для усіх тіл, що знаходяться в тепловій рівновазі. Можливість введення поняття температури виходить з досліду і носить назву нульового закону термодинаміки.
Для виміру температури використовуються фізичні прилади - термометри, в яких про величину температури судять по зміні якого-небудь фізичного параметра. Для створення термометра необхідно вибрати термометричну речовину (наприклад, ртуть або спирт) і термометричну величину, що характеризує властивість речовини (наприклад, довжина ртутного або спиртового стовпчика). У різних конструкціях термометрів використовуються різноманітні фізичні властивості речовини (наприклад, зміна лінійних розмірів твердих тіл або зміна електричного опору провідників при нагріванні).
Термометри мають бути відкалібровані. Для цього їх приводять в тепловий контакт з тілами, температури яких вважаються заданими. Найчастіше використовують прості природні системи, в яких температура залишається незмінною, незважаючи на теплообмін з довкіллям - це суміш льоду і води і суміш води і пари при кипінні при нормальному атмосферному тиску.
За температурною шкалою Цельсія точці плавлення льоду приписується температура 0°С, а точці кипіння води - 100°С. Зміна довжини стовпа рідини в капілярах термометра на одну соту довжини між відмітками 0°С і 100°С приймається рівним 1°С. У ряді країн (США) широко використовується шкала Фаренгейта (TF), в якій температура замерзаючої води приймається рівною 32°F, а температура кипіння води 212°F. Отже,
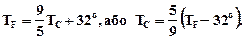
Особливе місце у фізиці займають газові термометри (рис. 2.29), в яких термометричною речовиною є розріджений газ (гелій, повітря) в посудині незмінного об'єму (V = const), а термометричною величиною - тиск газу p. Дослід показує, що тиск газу (при V = const) росте із зростанням температури, виміряної за шкалою Цельсія.

Рисунок 2.29.
Щоб проградуювати газовий термометр постійного об'єму, можна виміряти тиск при двох значеннях температури (наприклад, 0°C і 100°C), нанести точки p0 і p100 на графік, а потім провести між ними пряму лінію (рис. 2.30). Використовуючи отриманий таким чином калібрувальний графік, можна визначати температури, що відповідають іншим значенням тиску. Екстраполюючи графік в область низьких тисків, можна визначити деяку "гіпотетичну" температуру, при якій тиск газу став би рівним нулю. Розрахунки показують, що ця температура рівна - 273,15°С і не залежить від властивостей газу. Неможливо експериментально отримати шляхом охолодження газ з нульовим тиском, оскільки при дуже низьких температурах усі гази переходять в рідкі або тверді стани.

Рисунок 2.30.
Англійський фізик У. Кельвін в 1848 р. запропонував використовувати точку нульового тиску газу для побудови нової температурної шкали (шкала Кельвіна). У цій шкалі одиниця виміру температури така ж, як і в шкалі Цельсія, але нульова точка змінена:
TК = TС + 273,15.
У СІ прийнято одиницю виміру температури за шкалою Кельвіна називати кельвіном і означати буквою K. Наприклад, кімнатна температура TС = 20 °С за шкалою Кельвіна рівна TК = 293,15 К.
Температурна шкала Кельвіна називається абсолютною шкалою температур. Вона виявляється найбільш зручною при побудові фізичних теорій.
Таким чином, тиск розрідженого газу в посудині постійного об'єму V змінюється прямо пропорційно його абсолютній температурі: p ~ T. З іншого боку, дослід показує, що при незмінних об'ємі V і температурі T тиск газу змінюється прямо пропорційно відношенню кількості речовини ν в цій посудині до об'єму V посудини

де N - число молекул в посудині,NA - стала Авогадро, n = N / V- концентрація молекул. Об'єднуючи ці співвідношення пропорційності, можна записати:
p = nkT,(2.11)
де k - деяка універсальна для усіх газів постійна величина. Її називають стала Больцмана, на честь австрійського фізика Л. Больцмана (1844-1906 рр.), одного з творців молекулярно-кінетичної теорії. Стала Больцмана - одна з фундаментальних фізичних констант. Її чисельне значення в СІ становить:
k = 1,38·10–23 Дж/К.
 Порівнюючи співвідношення p = nkTз основним рівнянням молекулярно-кінетичної теорії газів, можна отримати:
Порівнюючи співвідношення p = nkTз основним рівнянням молекулярно-кінетичної теорії газів, можна отримати:
(2.12)
Середня кінетична енергія хаотичного руху молекул ідеального газу прямо пропорційна абсолютній температурі.
Таким чином, температура є міра середньої кінетичної енергії поступального руху молекул.
§25. Розподіл молекул за швидкостями
У попередніх параграфах підкреслювалася безладність, або хаотичність молекулярних рухів. Проте в 1860 році англійський фізик Дж. Максвелл, виходячи з основних положень молекулярно-кінетичної теорії, вивів точний закон, якому підпорядковані швидкості молекул газоподібного тіла (причому передбачається, що усі молекули газу однакові і що температура в усіх частинах газу також однакова). Розподіл молекул газу за швидкостями представлено на рисунку 2.31. По осі абсцис відкладаються різні значення швидкості молекул газу від нуля до деякої максимальної величини, а по осі ординат - відносне число молекул, швидкості яких лежать в інтервалі від v до v + Δv. Це число дорівнює площі виділеного на рисунку 2.31 стовпчика.
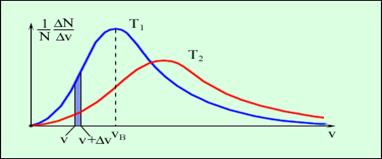
Рисунок 2.31.
Розподіл молекул за швидкостями. T2 > T1.
З графіку розподілу молекул за швидкостями виходить:
1. Число молекул, що мають малі швидкості дуже мале по відношенню до усього числа молекул газу.
2. Дуже мало також кількість молекул, що мають дуже великі швидкості.
3. Є одне значення швидкості, яке зустрічається частіше за інші значення, так звана найбільш ймовірна швидкість. vйм. Цьому значенню відповідає максимум кривої розподілу.
4. Великий відсоток усіх молекул мають швидкості, що не дуже сильно відрізняється від найбільш ймовірної швидкості, тому в деяких спрощених розрахунках можна приймати, що усі молекули мають приблизно одну і ту ж швидкість.
 Аналітично закон розподілу молекул за швидкостями виражається формулою:
Аналітично закон розподілу молекул за швидкостями виражається формулою:
(2.13)
де f(v) - функція розподілу, N - загальне число молекул у заданій масі газу, dN - число молекул, швидкості яких лежать в інтервалі від v до v + Δv, А - величина, яка залежить від температури газу і маси молекули.
На рисунку 2.31. показано дві криві розподілу швидкостей при різних температурах. Червона, більш полога крива, показує розподіл швидкостей за законом Максвелла при вищій температурі, ніж температура, до якої відноситься перша (синя) крива. Зіставлення цих двох кривих наочно виявляє властивості рівняння Максвелла. Видно, що при підвищенні температури росте найбільш ймовірна швидкість (максимум кривий розподіли зрушується направо); це відповідає тій обставині, що при підвищенні температури швидкості молекул зростають. Крива Максвелла при підвищенні температурі стає біль пологою: це означає, що при підвищенні температури розподіл молекул за швидкостями стає більш рівномірним.
Швидкість, при якій функція розподілу максимальна, називається найбільш ймовірною швидкістю. Її значення можна знайти, про диференціювавши функцію розподілу по змінній vі прирівнявши результат до нуля.
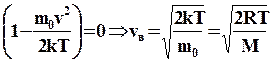 .
.
 Використовуючи вираз
Використовуючи вираз 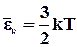 , і вираз ,
, і вираз ,
отримаємо значення середньої квадратичної швидкості:

. (2.14)
Середня швидкість молекул (середня арифметична швидкість) визначається по формулі

.

(2.15)
Виходячи із співвідношень найбільш ймовірної, середньої квадратичної і середньої арифметичної швидкостей можна записати співвідношення:
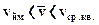
vcр ≈ 0,92 vcр.кв. vйм ≈ 0,815 vcр.кв.
У таблиці 2.1 представлений розподіл за швидкостями молекул азоту при кімнатній температурі.
Таблиця 2.1
| Область швидкостей м/с | Відсоток загального числа молекул, що мають швидкості, що знаходяться у вказаних інтервалах |
| 0 0 <v <100 | |
| 100 <v <300 | |
| 300 <v <500 | |
| 500 <v <700 | |
| 700 <v <900 | |
| 900 <v .. |
Дата добавления: 2016-10-17; просмотров: 1962;
