Определение деформаций статически неопределимых балок.
После того, как определены опорные реакции, построены эпюры изгибающих моментов и поперечных сил, подобраны сечения статически неопределимой балки, определение ее деформаций ничем- не отличается от таких же вычислений для статически определимой балки.
Необходимо лишь отметить, что в этом случае мы будем иметь избыточное число уравнений для определения постоянных интегрирования. Этот избыток равен числу лишних неизвестных. Избыточные уравнения при правильно найденных реакциях обратятся в, тождества, ибо они уже и были использованы при нахождении лишних неизвестных. Так для балки, с левым (А), жесткозащемленным и правым (В), шарнирноопертыми концами с пролетом l, получим следующее дифференциальное уравнение изогнутой оси:
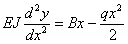
Интегрируем:
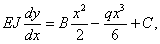
| (а) |
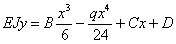
| (b) |
Постоянных интегрирования две, условий же для их определения можно написать три, а именно:
в точке А при 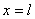 прогиб
прогиб 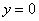 и угол поворота
и угол поворота 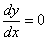 ;
;
В х=0 у = 0.
Третье из этих уравнений обратится в тождество, ибо оно уже было нами использовано при составлении дополнительного уравнения, из которого мы нашли для В значение 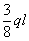 . Заметим, что мы могли бы использовать уравнение изогнутой оси балки для нахождения лишней неизвестной. Приняв за лишнюю неизвестную реакцию В, составим и проинтегрируем дифференциальное уравнение изогнутой оси; получим формулы (а) и (b).
. Заметим, что мы могли бы использовать уравнение изогнутой оси балки для нахождения лишней неизвестной. Приняв за лишнюю неизвестную реакцию В, составим и проинтегрируем дифференциальное уравнение изогнутой оси; получим формулы (а) и (b).
Используя граничные условия в точках А и В, получим три уравнения, из которых найдем реакцию В и постоянные интегрирования С и D.
Лекция № 37. Расчет статически неопределимых стержневых систем
Дата добавления: 2016-10-17; просмотров: 642;
