Определение деформаций балок переменного сечения.
При определении прогибов и углов поворота для балок с переменным сечением надлежит иметь в виду, что жесткость такой балки является функцией от х. Поэтому дифференциальное уравнение изогнутой оси принимает вид
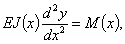
где J(x) — переменный момент инерции сечений балки.
До интегрирования этого уравнения можно выразить J(x) надлежащей подстановкой через J, т. е. через момент инерции того; сечения, где действует 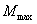 ; после этого вычисления производятся так же, как и.для балок постоянного сечения.
; после этого вычисления производятся так же, как и.для балок постоянного сечения.
Покажем это на примере, разобранном выше. Определим прогиб балки равного сопротивления, защемленной одним концом, нагруженной на другом конце силой Р и имеющей постоянную высоту. Начало координат выберем на свободном конце балки.
Тогда
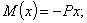
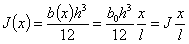
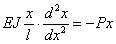
Дифференциальное уравнение принимает вид:
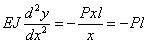
Интегрируем два раза:
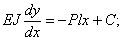
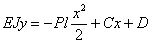
Для определения постоянных интегрирования имеем условия: точке А при 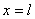 прогиб
прогиб 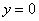 и угол поворота
и угол поворота 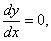 или
или
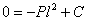 и
и 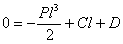
отсюда
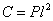 и
и 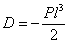
Выражения для у и 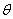 принимают вид;
принимают вид;
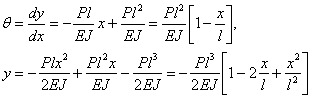
Наибольший прогиб на свободном конце балки В получится при 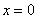 : он равен
: он равен
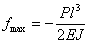
Если бы мы всю балку сделали постоянного сечения с моментом инерции J, то наибольший прогиб был бы
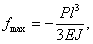
т. е. в 1 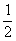 раза меньше.
раза меньше.
Таким образом, балки переменного сечения обладают большей гибкостью по сравнению с балками постоянной жесткости при одинаковой с ними прочности. Именно поэтому, а не только ради экономии материала, они и применяются в таких конструкциях, как рессоры.
Лекция № 31. Расчет балки на упругом основании.
Общие понятия.
К числу статически неопределимых балок может быть отнесена балка на упругом основании. Так называется балка, опирающаяся по всей своей длине (Рис.1) на упругое основание, оказывающее в каждой точке на балку реакцию, пропорциональную у — прогибу балки в этой точке. Коэффициент пропорциональности обозначается буквой k.
Введение предположения о пропорциональности реакций прогибу является приближением, хотя и достаточно близким к действительным условиям.

Рис.1. Расчетная схема балки на упругом основании.
Предложение ввести в расчет коэффициент пропорциональности к, именуемый «коэффициентом постели», было впервые сделано русским академиком Николаем Ивановичем Фуссом в 1801 году. Принимая это предположение, получаем, что интенсивность реакции основания в каждой точке сила равна ky и измеряется в единицах силы и длины; размерность коэффициента k при этом будет сила и квадрат длины. Будем считать, что основание оказывает реакцию при прогибах балки как вниз, так и вверх.
На практике задачи о расчете балки на упругом основании встречаются в железнодорожном деле (рельс, шпала), в строительстве — фундаменты различных сооружений, передающие нагрузку на грунт.
Статически неопределимой такая балка будет потому, что условие статики— сумма нагрузок равна всей реакции основания — не дает возможности установить распределение этой реакции по длине балки, а значит, вычислить изгибающие моменты и поперечные силы.
Интенсивность реакции в каждой точке связана с прогибами балки. Поэтому для решения задачи необходимо найти сначала уравнение изогнутой оси 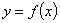 , а уже затем формулы для вычисления изгибающего момента и поперечной силы. Ход решения оказывается обратным обычному.
, а уже затем формулы для вычисления изгибающего момента и поперечной силы. Ход решения оказывается обратным обычному.
Найдем уравнение изогнутой оси для балки постоянного сечения, лежащей на упругом основании и нагруженной сосредоточенными силами 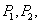 ... (Рис.1). Начало координат возьмем в любой точке, ось х направим вправо, ось у вертикально вверх. Направление нагрузок вверх будем считать положительным. Напишем обычное дифференциальное уравнение изгиба
... (Рис.1). Начало координат возьмем в любой точке, ось х направим вправо, ось у вертикально вверх. Направление нагрузок вверх будем считать положительным. Напишем обычное дифференциальное уравнение изгиба
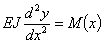
Так как М(х) нам неизвестен, то постараемся связать прогибы непосредственно с нагрузкой, для этого дифференцируем дважды предыдущее уравнение:
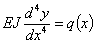
| (1) |
где q(x)—интенсивность сплошной нагрузки, действующей на балку в сечении с абсциссой х.
Сплошной нагрузкой для нашей балки является лишь реакция упругого основания. Интенсивность ей пропорциональна прогибам; эта нагрузка направлена вверх, т. е. положительна, когда прогибы идут вниз, т. е. отрицательны, и наоборот. Таким образом, эта нагрузка имеет знак, обратный знаку прогибов:
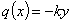
Тогда
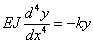
| (2) |
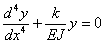
| (3) |
Если обозначить 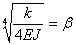 , то общий интеграл уравнения (25.3) имеет вид:
, то общий интеграл уравнения (25.3) имеет вид: 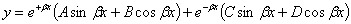 (25.4)
(25.4)
Постоянные А, В, С, D должны быть определены в каждом частном случае нагрузки и длины балки. Величина 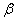 имеет измерение обратное длине.
имеет измерение обратное длине.
Дата добавления: 2016-10-17; просмотров: 769;
