НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ. ТЕНЗОР НАПРЯЖЕНИЙ
Вектор напряженийpn является физическим объектом, имеющим длину, направление и точку приложения. В этом смысле он обладает векторными свойствами. Однако этому объекту присущи некоторые свойства, не характерные для векторов. В частности, величина и направление вектора напряжений зависят от ориентации вектора n нормали бесконечно малого элемента поверхности dF. Совокупность всех возможных пар векторовп, рn в точке определяет напряженное состояние в данной точке. Однако для полного описания напряженного состояния в точке нет необходимости задавать бесконечное множество направлений вектораn, достаточно определить векторы напряжений на трех взаимно перпендикулярных элементарных площадках. Напряжения на произвольно ориентированных площадках могут быть выражены через эти три вектора напряжений. В дальнейшем лектор умышленно меняет ориентацию координат. Так, что ось Z – продольная ось бруса, а X и Y – координаты любой точки его поперечного сечения.
Проведем через точку М три взаимно перпендикулярных плоскости с векторами нормалей, направления которых совпадают с направлениями координатных осей. Элементарные площадки образуем дополнительными сечениями, параллельными исходным плоскостям и отстоящими от них на бесконечно малые расстояния dx, dy, dz. В результате в окрестности точки М получим бесконечно малый параллелепипед, поверхность которого образована элементарными площадками dFх=dydz, dFн==dxdz, dFя=dxdy. Векторы напряжений px,py, pz, действующие на элементарных площадках, показаны на рис. 5.
Разложим каждый вектор напряжений на составляющие вдоль координатных осей (рис. 6). На каждой площадке действует одно нормальное напряжение  ,
, 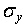 ,
, 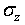 , где индекс обозначает направление вектора нормали к площадке и два касательных напряжения
, где индекс обозначает направление вектора нормали к площадке и два касательных напряжения 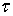 с двумя индексами, из которых первый указывает направление действия компоненты напряжения, второй—направление вектора нормали к площадке.
с двумя индексами, из которых первый указывает направление действия компоненты напряжения, второй—направление вектора нормали к площадке.
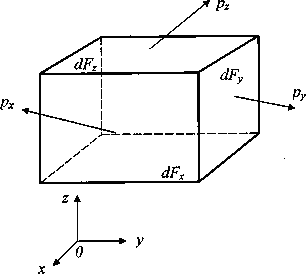
Рис. 5. Равновесное состояние бесконечно-малого параллелепипеда
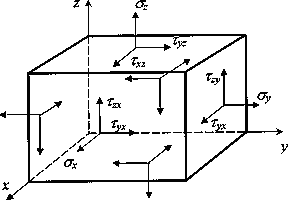
Рис.6. Компоненты тензора напряженного состояния
Совокупность девяти компонент напряжений (по три на каждой из трех взаимно перпендикулярных площадок) представляет собой некоторый физический объект, называемый тензором напряжений в точке. Тензор можно представить в виде матрицы, соответствующим образом упорядочив девять компонент:
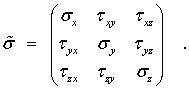
Для компонент тензора напряжений общепринятым является следующее правило знаков: компонента считается положительной, если на площадке с положительной внешней нормалью (т. е. направленной вдоль одной из координатных осей) эта компонента направлена в сторону положительного направления соответствующей оси. На рис. 6 все компоненты тензора напряжений изображены положительными. На площадках с отрицательной внешней нормалью (грани параллелепипеда, не видимые на рис. 5 и 6) положительная компонента направлена в противоположном направлении. Напряжения на трех взаимно ортогональных площадках с отрицательными направлениями нормалей также характеризуют напряженное состояние в точке. Эти напряжения, являющиеся компонентами тензора напряжений, определяются аналогично напряжениям на площадках с положительной нормалью. Они обозначаются теми же символами и имеют положительное направление, обратное изображенному на рис. 6.
Лекция № 6. Свойства тензора напряжений. Главные напряжения
Тензор напряжений обладает свойством симметрии. Для доказательства этого свойства рассмотрим приведенный в лекции 5 элементарный параллелепипед с действующими на его площадках компонентами тензора напряжений. Так как тело находится в равновесии, следовательно, находится в равновесии любая его часть, в том числе и элементарный объем. Запишем одно из шести уравнений равновесия этого объема, а именно — сумму моментов всех сил относительно оси Ох. Все силы, кроме двух, либо не создают момента относительно ocи Ох, либо взаимно уничтожаются. Отличные от нуля моменты создают компоненты 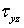 (верхняя грань) и
(верхняя грань) и  (права грань):
(права грань):
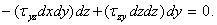
После сокращения на элемент объема dV=dxdydz получим

Аналогично, приравнивая нулю сумму моментов всех сил относительно осей Оу и Ог, получим еще два соотношения
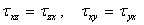
Эти условия симметрии и тензора напряжений называются также условиями парности касательных напряжений: касательные напряжения, действующие по двум взаимно перпендикулярным площадкам в направлениях, ортогональных ребру, образованному пересечением этих площадок, равны по величине. С учетом этих свойств из девяти компонент тензора напряжений независимыми оказываются шесть компонент.
Покажем теперь, что компоненты тензора напряжений определенные для трех взаимно перпендикулярных площадок, полностью характеризуют напряженное состояние в точке, т. е. позволяют вычислить компоненты вектора напряжений на площадках, произвольно ориентированных относительно выбранной системы координат. Для этого рассмотрим элементарный объем, образованный сечением параллелепипеда, изображенного на рис. 1, плоскостью, пересекающей координатные оси и имеющей единичный вектор нормали

Рис.1. Элементарный четырехгранник с компонентами напряженного состояния.
п с компонентами nx, ny, nz. На гранях полученного таким образом бесконечно малого тетраэдра действуют напряжения, показанные на рис. 1. При этом вектор напряжений pn на наклонной площадке разложен па составляющие рx, рy, рz вдоль координатных осей. Площади граней, ортогональных координатным осям и вектору нормали, обозначим соответственно dFx, dFy, dFz, dF. Эти площади связаны между собой соотношениями
| dFx=dFnx, dFy=dFny, dFz=dFnz | (1) |
вытекающими из того, что грани, ортогональные координатным осям, есть проекции наклонной площадки на соответствующую координатную плоскость.
Проектируя силы, действующие на гранях элементарного тетраэдра, на координатные оси, получим уравнения равновесия для рассматриваемого объема. Например, проекции всех поверхностных сил на ось Ох дают
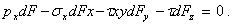
С учетом соотношений (1) после сокращения на dF получим уравнение, связывающее проекцию рx вектора напряжений с соответствующими компонентами тензора напряжений. Объединяя это уравнение с двумя аналогичными уравнениями, полученными проектированием сил на оси Оy и Оz, приходим к следующим соотношениям
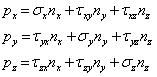
| (2) |
носящим название формул Коши. Эти формулы определяют вектор напряжений на произвольно выбранной площадке с вектором п через компоненты тензора напряжений.
Формулы (2) позволяют вычислить через компоненты тензора напряжений
полное напряжение
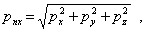
| (3) |
нормальное напряжение
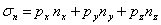
| (4) |
и касательное напряжение

| (5) |
Среди всех возможных направлений вектора нормали n существуют такие направления, для которых вектор напряженийpn параллелен вектору п. На соответствующих площадках действуют только нормальные напряжения, а касательные напряжения отсутствуют. Такие площадки называются главными, а нормальные напряжения на этих площадках называются главными напряжениями. Пусть площадка с единичным вектором нормали является главной. Условия коллинеарности векторов pn и n есть условия пропорциональности их компонент:

С учетом формул Коши получим систему линейных однородных уравнений относительно неизвестных компонент nx, ny, nz вектора нормали к главной площадке

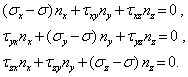
Эта система уравнений имеет ненулевое решение, если определитель, составленный из коэффициентов уравнений, обращается в нуль:
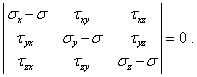
| (6) |
Раскрывая определитель, приходим к кубическому уравнению относительно главного напряжения 
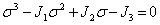
| (7) |
Здесь введены обозначения

| (8) |

| (9) |

|
Уравнение (7) называется характеристическим уравнением для тензора напряжений. Коэффициенты (9) этого уравнения называются инвариантами тензора напряжений. Решение кубического уравнения (8) имеет три вещественных корня  которые обычно упорядочиваются
которые обычно упорядочиваются 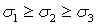 .
.
Каждому значению 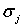 (j=1, 2, 3) соответствует векторn j,характеризующий положение j-й главной площадки, с компонентами n j1, n j2, n j3. Для нахождения этих компонент достаточно в уравнения подставить найденное значение
(j=1, 2, 3) соответствует векторn j,характеризующий положение j-й главной площадки, с компонентами n j1, n j2, n j3. Для нахождения этих компонент достаточно в уравнения подставить найденное значение 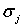 и решить любые два из этих уравнений совместно с условием нормировки
и решить любые два из этих уравнений совместно с условием нормировки

Главные напряжения обладают важным свойством: по сравнению со всеми другими площадками нормальные напряжения на главных площадках принимают экстремальные значения. Для доказательства этого свойства достаточно исследовать на экстремум нормальное напряжение как функцию nx, ny, nz при дополнительном ограничении. Можно показать, что три главные площадки, соответствующие главным напряжениям  , взаимно перпендикулярны или, что то же самое, векторы nj и nk, соответствующие различным значениям j и k —; ортогональны. Условие ортогональности имеет вид
, взаимно перпендикулярны или, что то же самое, векторы nj и nk, соответствующие различным значениям j и k —; ортогональны. Условие ортогональности имеет вид

| (10) |
Кубическое уравнение (8) можно переписать в виде
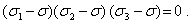
| (11) |
Приводя это уравнение к виду (8), получим следующие выражения для инвариантов (9) через главные напряжения:
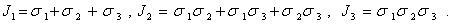
| (12) |
Термин «инвариантность» обозначает независимость некоторой величины от выбора системы координат.
Введем среднее напряжение по формуле
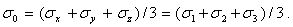
| (13) |
Тензор напряжений можно представить в виде суммы двух тензоров 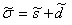 , где
, где
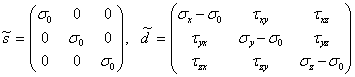
| (14) |
Первый тензор называется шаровым, он характеризует изменение объема тела без изменения его формы. Второй тензор, называемый девиатором, характеризует изменение формы. Особенностью девиатора напряжений является равенство нулю его первого инварианта:
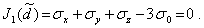
| (15) |
Найдем положение площадок, на которых касательные напряжения принимают экстремальные значения. Для этого нужно отыскать экстремумы касательного напряжения. Экстремальные касательные напряжения действуют на площадках, параллельных одной из главных осей и образующих с двумя другими осями угол  . По величине эти напряжения равны
. По величине эти напряжения равны

| (16) |
При этом на площадках с экспериментальными касательными напряжениями присутствуют нормальные напряжения, которые равны
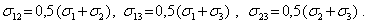
Фигура, которую образуют площадки с экстремальными касательными напряжениями, изображена на рис. 2. Она принадлежит к классу параллелоэдров и представляет собой 12-гранник с гранями в виде ромбов, отношение диагоналей которых равно 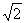 .
.

Рис.2. Параллепоэдр распределения экстремальных касательных напряжений
Таким образом, общая теория напряженного состояния позволяет охватывать, в целом, весь комплекс видов сопротивлений, как простого, так и сложного характера.
Лекция № 7. Плоское напряженное состояние
Рассмотрим важный для приложений случай плоского напряженного состояния, реализуемого, например, в плоскости Oyz. Тензор напряжений в этом случае имеет вид
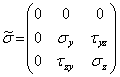
Геометрическая иллюстрация представлена на рис.1. При этом площадки х=const являются главными с соответствующими нулевыми главными напряжениями. Инварианты тензора напряжений равны 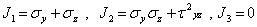 , а характеристическое уравнение принимает вид
, а характеристическое уравнение принимает вид
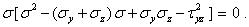
Корни этого уравнения равны

| (1) |
Нумерация корней произведена для случая 
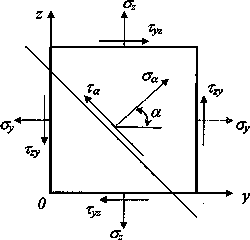
Рис.1. Исходное плоское напряженное состояние.

Рис.2. Позиция главных напряжений
Произвольная площадка характеризуется углом  на рис. 1, при этом вектор п имеет компоненты:
на рис. 1, при этом вектор п имеет компоненты: 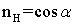 ,
, 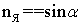 , nх=0. Нормальное и касательное напряжения на наклонной площадке выражаются через угол
, nх=0. Нормальное и касательное напряжения на наклонной площадке выражаются через угол  следующим образом:
следующим образом:

| (2) |
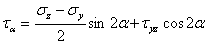
| (3) |
Так как на главных площадках касательное напряжение отсутствует, то, приравнивая нулю выражение (3), получим уравнение для определения угла  между нормалью п и осью Оу
между нормалью п и осью Оу

| (4) |
Наименьший положительный корень уравнения (4) обозначим через 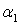 . Так как tg(х)—периодическая функция с периодом
. Так как tg(х)—периодическая функция с периодом 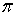 , то имеем два взаимно ортогональных направления, составляющие углы
, то имеем два взаимно ортогональных направления, составляющие углы 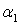 и
и 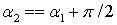 с осью Оу. Эти направления соответствуют взаимно перпендикулярным главным площадкам (рис. 2).
с осью Оу. Эти направления соответствуют взаимно перпендикулярным главным площадкам (рис. 2).
Если продифференцировать соотношение (2) по  и приравнять производную нулю, то придем к уравнению (4), что доказывает экстремальность главных напряжений.
и приравнять производную нулю, то придем к уравнению (4), что доказывает экстремальность главных напряжений.
Для нахождения ориентации площадок с экстремальными касательными напряжениями приравняем нулю производную от выражения
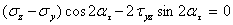 ,
,
откуда получим

| (5) |
Сравнивая соотношения (4) и (5), находим, что
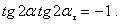
Это равенство возможно, если углы 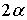 и
и 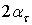 отличаются на угол
отличаются на угол 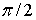 . Следовательно, направления площадок с экстремальными касательными напряжениями отличаются от направлений главных площадок на угол
. Следовательно, направления площадок с экстремальными касательными напряжениями отличаются от направлений главных площадок на угол  (рис. 3).
(рис. 3).

Рис.3. Экстремальность касательных напряжений
Величины экстремальных касательных напряжений получим после подстановки (5) в соотношение (3) с использованием формул
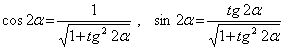 .
.
После некоторых преобразований получим

Сравнивая это выражение с полученными ранее значениями главных напряжений (2.21), выразим экстремальные касательные напряжения через главные напряжения
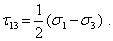
Аналогичная подстановка в (2) приводит к выражению для нормальных напряжений на площадках с 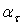
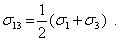
Полученные соотношения позволяют проводить направленно-ориентированный расчет конструкций на прочность в случае плоского напряженного состояния.
ТЕНЗОР ДЕФОРМАЦИИ
Рассмотрим вначале случай плоской деформации (рис. 4). Пусть плоский элемент MNPQ перемещается в пределах плоскости и деформируется (изменяет форму и размеры). Координаты точек элемента до и после деформации отмечены на рисунке.
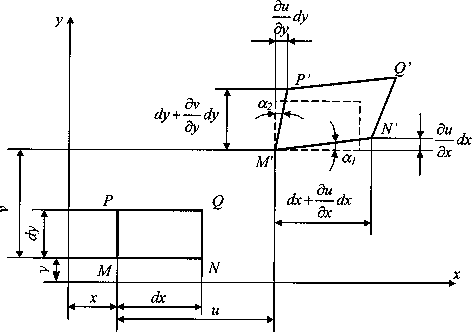
Рис.4. Плоская деформация.
По определению относительная линейная деформация в точке М в направлении оси Ох равна
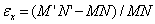
Из рис. 4 следует
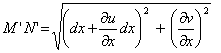
Учитывая, что MN=dx, получим

В случае малых деформаций, когда 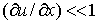 ,
,  , можно пренебречь квадратичными слагаемыми. С учетом приближенного соотношения
, можно пренебречь квадратичными слагаемыми. С учетом приближенного соотношения
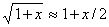
справедливого при x<<1, окончательно для малой деформации получим

Угловая деформация 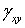 определяется как сумма углов
определяется как сумма углов 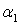 и
и 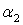 (4). В случае малых деформаций
(4). В случае малых деформаций

Для угловой деформации 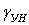 имеем
имеем
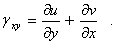
Проводя аналогичные выкладки в общем случае трехмерной деформации, имеем девять соотношений
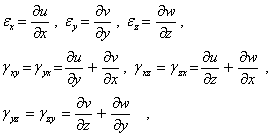
| (6) |
связывающих линейные и угловые деформации с перемещениями. Эти соотношения носят название соотношений Коши.
Три линейных и шесть угловых деформаций (6) образуют тензор малых деформаций

| (7) |
Этот тензор полностью определяет деформированное состояние твердого тела. Он обладает теми же свойствами, что и тензор напряжений. Свойство симметрии непосредственно следует из определения угловых деформаций. Главные значения и главные направления, а также экстремальные значения угловых деформаций и соответствующие им направления находятся теми же методами, что и для тензора напряжений.
Инварианты тензора деформаций определяются аналогичными формулами, причем первый инвариант тензора малых деформаций имеет ясный физический смысл. До деформации его объем равен dV0 =dxdydz. Если пренебречь деформациями сдвига, которые изменяют форму, а не объем, то после деформации ребра будут иметь размеры
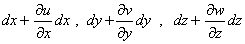
(рис. 4), а его объем будет равен
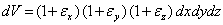 .
.
Относительное изменение объема
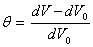
в пределах малых деформаций составит
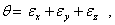
что совпадает с определением первого инварианта. Очевидно, что изменение объема есть физическая величина, не зависящая от выбора системы координат.
Так же, как и тензор напряжений, тензор деформаций можно разложить на шаровой тензор и девиатор. При этом первый инвариант девиатора равен нулю, т. е. девиатор характеризует деформацию тела без изменения его объема.
Лекция № 8. Упругость и пластичность. Закон Гука
Действие внешних сил на твердое тело приводит к возникновению в точках его объема напряжений и деформаций. При этом напряженное состояние в точке, связь между напряжениями на различных площадках, проходящих через эту точку, определяются уравнениями статики и не зависят от физических свойств материала. Деформированное состояние, связь между перемещениями и деформациями устанавливаются с привлечением геометрических или кинематических соображений и также не зависят от свойств материала. Для того чтобы установить связь между напряжениями и деформациями, необходимо учитывать реальные свойства материала и условия нагружения. Математические модели, описывающие соотношения между напряжениями и деформациями, разрабатываются на основе экспериментальных данных. Эти модели должны с достаточной степенью точности отражать реальные свойства материалов и условия нагружения.
Наиболее распространенными для конструкционных материалов являются модели упругости и пластичности. Упругость — это свойство тела изменять форму и размеры под действием внешних нагрузок и восстанавливать исходную конфигурацию при снятии нагрузок. Математически свойство упругости выражается в установлении взаимно однозначной функциональной зависимости между.компонентами тензора напряжений и тензора деформаций. Свойство упругости отражает не только свойства материалов, но и условия нагружения. Для большинства конструкционных материалов свойство упругости проявляется при умеренных значениях внешних сил, приводящих к малым деформациям, и при малых скоростях нагружения, когда потери энергии за счет температурных эффектов пренебрежимо малы. Материал называется линейно-упругим, если компоненты тензора напряжений и тензора деформаций связаны линейными соотношениями.
При высоких уровнях нагружения, когда в теле возникают значительные деформации, материал частично теряет упругие свойства: при разгрузке его первоначальные размеры и форма полностью не восстанавливаются, а при полном снятии внешних нагрузок фиксируются остаточные деформации. В этом случае зависимость между напряжениями и деформациями перестает быть однозначной. Это свойство материала называется пластичностью. Накапливаемые в процессе пластического деформирования остаточные деформации называются пластическими.
Высокий уровень нагружения может вызвать разрушение, т. е. разделение тела на части. Твердые тела, выполненные из различных материалов, разрушаются при разной величине деформации. Разрушение носит хрупкий характер при малых деформациях и происходит, как правило, без заметных пластических деформаций. Такое разрушение характерно для чугуна, легированных сталей, бетона, стекла, керамики и некоторых других конструкционных материалов. Для малоуглеродистых сталей, цветных металлов, пластмасс характерен пластический тип разрушения при наличии значительных остаточных деформаций. Однако подразделение материалов по характеру разрушения на хрупкие и пластичные весьма условно, оно обычно относится к некоторым стандартным условиям эксплуатации. Один и тот же материал может вести себя в зависимости от условий (температура, характер нагружены я, технология изготовления и др.) как хрупкий или как пластичный. Например, пластичные при нормальной температуре материалы разрушаются как хрупкие при низких температурах. Поэтому правильнее говорить не о хрупких и пластичных материалах, а о хрупком или пластическом состоянии материала.
Пусть материал является линейно-упругим и изотропным. Рассмотрим элементарный объем, находящийся в условиях одноосного напряженного состояния (рис. 1), так что тензор напряжений имеет вид
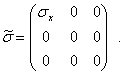
При таком нагружении происходит увеличение размеров в направлении оси Ох, характеризуемое линейной деформацией  , которая пропорциональна величине напряжения
, которая пропорциональна величине напряжения

| (1) |

Рис.1. Одноосное напряженное состояние
Это соотношение является математической записью закона Гука, устанавливающего пропорциональную зависимость между напряжением и соответствующей линейной деформацией при одноосном напряженном состоянии. Коэффициент пропорциональности E называется модулем продольной упругости или модулем Юнга. Он имеет размерность напряжений.
Наряду с увеличением размеров в направлении действия; же напряжения 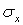 происходит уменьшение размеров в двух ортогональных направлениях (рис. 1). Соответствующие деформации обозначим через
происходит уменьшение размеров в двух ортогональных направлениях (рис. 1). Соответствующие деформации обозначим через 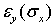 и
и 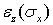 , причем эти деформации отрицательны при положительных
, причем эти деформации отрицательны при положительных 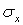 и пропорциональны
и пропорциональны 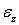 :
:
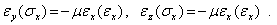
| (2) |
Коэффициент пропорциональности 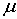 называется коэффициентом Пуассона, который в силу изотропности материала одинаков для обоих ортогональных направлений.
называется коэффициентом Пуассона, который в силу изотропности материала одинаков для обоих ортогональных направлений.
Соотношения, аналогичные (1) и (2), в случае одноосного нагружения в направлении осей Оу, Ог напряжением  ,
, 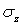 , соответственно имеют вид
, соответственно имеют вид
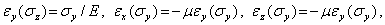
| (3) |
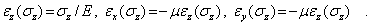
| (4) |
При одновременном действии напряжений по трем ортогональным осям, когда отсутствуют касательные напряжения, для линейно-упругого материала справедлив принцип суперпозиции (наложения решений):
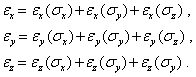
С учетом формул (1 — 4) получим
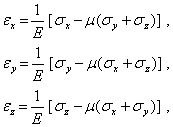
| (5) |
Касательные напряжения вызывают угловые деформации, причем при малых деформациях они не влияют на изменение линейных размеров, и следовательно, на линейные деформации. Поэтому они справедливы также в случае произвольного напряженного состояния и выражают так называемый обобщенный закон Гука.
Угловая деформация 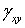 обусловлена касательным напряжением
обусловлена касательным напряжением 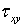 , а деформации
, а деформации 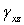 и
и 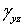 — соответственно напряжениями
— соответственно напряжениями 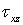 и
и 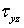 . Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости
. Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости
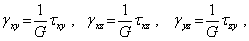
| (6) |
которые выражают закон Гука при сдвиге. Коэффициент пропорциональности G называется модулем сдвига. Существенно, что нормальное напряжение не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними (рис. 1).
Линейная зависимость существует также между средним напряжением (2.18), пропорциональным первому инварианту тензора напряжений, и объемной деформацией (2.32), совпадающей с первым инвариантом тензора деформаций:
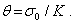
| (7) |

Рис.2. Плоская деформация сдвига
Соответствующий коэффициент пропорциональности К называется объемным модулем упругости.
В формулы (1 — 7) входят упругие характеристики материала Е, 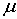 , G и К, определяющие его упругие свойства. Однако эти характеристики не являются независимыми. Для изотропного материала независимыми упругими характеристиками являются две, в качестве которых обычно выбираются модуль упругости Е и коэффициент Пуассона
, G и К, определяющие его упругие свойства. Однако эти характеристики не являются независимыми. Для изотропного материала независимыми упругими характеристиками являются две, в качестве которых обычно выбираются модуль упругости Е и коэффициент Пуассона 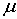 . Чтобы выразить модуль сдвига G через Е и
. Чтобы выразить модуль сдвига G через Е и 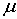 , рассмотрим плоскую деформацию сдвига под действием касательных напряжений
, рассмотрим плоскую деформацию сдвига под действием касательных напряжений 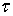 (рис. 2). Для упрощения выкладок используем квадратный элемент со стороной а. Вычислим главные напряжения
(рис. 2). Для упрощения выкладок используем квадратный элемент со стороной а. Вычислим главные напряжения 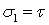 ,
,  . Эти напряжения действуют на площадках, расположенных под углом
. Эти напряжения действуют на площадках, расположенных под углом  к исходным площадкам. Из рис. 2 найдем связь между линейной деформацией
к исходным площадкам. Из рис. 2 найдем связь между линейной деформацией 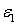 в направлении действия напряжения
в направлении действия напряжения 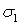 и угловой деформацией
и угловой деформацией 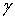 . Большая диагональ ромба, характеризующая деформацию
. Большая диагональ ромба, характеризующая деформацию 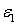 , равна
, равна

Для малых деформаций

С учетом этих соотношений
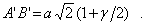
До деформации эта диагональ имела размер  . Тогда будем иметь
. Тогда будем иметь
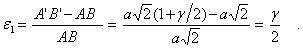
Из обобщенного закона Гука (5) получим
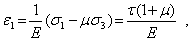
откуда
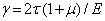
Сравнение полученной формулы с записью закона Гука при сдвиге (6) дает

| (8) |
Сложим три соотношения упругости (5)
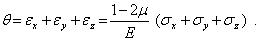
| (9) |
В итоге получим
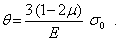
Сравнивая это выражение с объемным законом Гука (7), приходим к результату
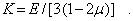
Механические характеристики Е, 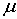 , G и К находятся после обработки экспериментальных данных испытаний образцов на различные виды нагрузок. Из физического смысла все эти характеристики не могут быть отрицательными. Кроме того, из последнего выражения следует, что коэффициент Пуассона для изотропного материала не превышает значения 1/2. Таким образом, получаем следующие ограничения для упругих постоянных изотропного материала:
, G и К находятся после обработки экспериментальных данных испытаний образцов на различные виды нагрузок. Из физического смысла все эти характеристики не могут быть отрицательными. Кроме того, из последнего выражения следует, что коэффициент Пуассона для изотропного материала не превышает значения 1/2. Таким образом, получаем следующие ограничения для упругих постоянных изотропного материала:
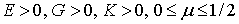
Предельное значение 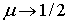 приводит к предельному значению
приводит к предельному значению 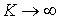 , что соответствует несжимаемому материалу (
, что соответствует несжимаемому материалу ( 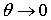 при
при 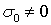 ). В заключение выразим из соотношений упругости (5) напряжения через деформации. Запишем первое из соотношений (5) в виде
). В заключение выразим из соотношений упругости (5) напряжения через деформации. Запишем первое из соотношений (5) в виде
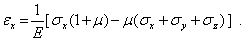
С использованием равенства (9) будем иметь
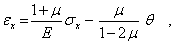
откуда

Аналогичные соотношения можно вывести для 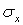 и
и  . В результате получим
. В результате получим

| (10) |
Здесь использовано соотношение (8) для модуля сдвига. Кроме того, введено обозначение

Дата добавления: 2016-10-17; просмотров: 3409;
