Некоторые фундаментальные понятия и определения
Рассмотрим три базовые концепции: действия, исходы и состояние природы. Под действием будем понимать решение или выбор из некоторого числа альтернатив, который игрок делает в некотором специфическом контексте, и это именно то, что мы стараемся предсказать. Предположение о целесообразности означает, что действие игрока ориентировано на достижение определенного исхода или/и во избежание определенного исхода. Таким образом, между действием и исходом существует определенная причинно-следственная связь. Связь эта, однако, не прямая, а опосредованная (иначе мы не имели бы игровой ситуации). А именно, необходимо ввести еще концепцию состояния природы, под которым понимаются такие внешние условия, при которых исход “И” достигается посредством действия “Д”.
Действия
Пусть aj обозначает одно из действий игрока (альтернативу с номером j), а A - множество всех допустимых действий: A={a1, a2, a3,...,aj,...}.
Предположим теперь, что игрок может выбирать одно и только одно действие из списка А. Тогда множество А является исчерпывающим или полным: в нем перечислены все возможности и одна из них должна быть реализована, а элементы множества А являются взаимоисключающими: игрок не может выбрать более одного действия. Когда, например, мы моделируем процесс голосования и изучаем вопрос, почему человек принимает (не принимает) участие в голосовании, мы используем множество А, состоящее только из двух элементов: A={a1 - голосовать, a2 - не голосовать}. Даже на таком примитивном уровне описания множество А является полным и взаимоисключающим. Любой избиратель вынужден осуществить одно из действий и не в состоянии осуществить оба сразу.
Исходы
Под целью можно понимать исход - объект, к которому стремится игрок. Обозначая исходы R={r1, r2, ..., rk,...}, на них налагаются те же ограничения, что и на действия. Множество R должно быть полным, а его элементы взаимоисключающими.
Анализируя результаты парламентских выборов при двухпартийной системе, мы можем сформировать следующее множество исходов: R={r1: победила партия 1, r2: победила партия 2, r3: ни одной из партий победить не удалось}. Однако, если нас интересует не только факт победы, но и счет, то элемент множества исходов в общем виде будет выглядеть как “партия 1 набрала v1 голосов, а партия 2 набрала v2”. Если мы станем перечислять все подобные исходы (перебирая все мыслимые комбинации v1 и v2), то число их окажется очень большим, хотя все еще конечным. Но если мы рассматриваем игру, в которой игроки вносят некоторые суммы в кассу своей партии, и размер взносов ничем не ограничен, то число исходов становится просто бесконечным.
Бесконечные и несчетные множества (в частности интервалы значений действительных чисел) имеют простую геометрическую интерпретацию и позволяют привлекать нашу геометрическую интуицию для интерпретации результатов.
Пример: партийный казначей для проведения предвыборной кампании распределяет фиксированную сумму денег, скажем Х, между тремя кандидатами.
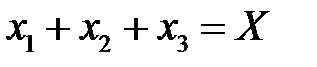
Рисунок 1 Бюджетный симплекс |
Все мыслимые способы дележа представлены на рисунке 1 точками, составляющими треугольник, называемый бюджетным симплексом.
Бюджетный симплекс - ограниченное и замкнутое множество.
Кроме того, оно выпуклое.
Выпуклым множеством называется такое, что если выбрать любые две точки, принадлежащие этому множеству и соединить их отрезком прямой, то весь отрезок тоже будет принадлежать множеству. Свойство выпуклости вполне понятно из следующих трех примеров:
| 
| 
|
| а) выпуклое множество | б) строго выпуклое множество | в) невыпуклое множество: точка А находится вне его. |
Итак, бюджетный симплекс - ограниченное, замкнутое и выпуклое множество.
Дата добавления: 2016-10-17; просмотров: 581;
