Расчет среднего квадратического отклонения 25 выборочных средних

| 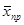 
|  - - 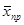 
| 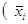 - -  2 2
| P | 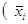 - -  2 2
|
| -30 | \ | ||||
| -25 | 2 | ||||
| -20 | |||||
| -15 | |||||
| -10 | 100 ' | ||||
| . 35 | -5 | ||||

| 
|
Сейчас мы располагаем всеми данными для расчета среднего квадратического отклонения: μ = 17,32 мин.
Величина среднего квадратического отклонения позволяет заранее предсказать, какое количество выборок в данной генеральной совокупности будут «плохими», т. е. отклонятся от средней на слишком большое расстояние, а сколько из них дадут приемлемые значения. Иными словами, ошибка выборки при условии, что она случайна, поддается априорному расчету. В нашем примере выборка (два человека из совокупности в пять человек) слишком мала, чтобы пытаться установить в ней какую-либо регулярность. Но сотни и тысячи
случайных выборок, точнее, параметры случайных выборок, распределяются в соответствии с законом, который называется законом нормального распределения. Его суть заключается в том, что наибольшее число выборочных средних располагается в середине ряда плотности распределения, а крайние значения маловероятны. Чем больше число наблюдений, тем ближе распределение выборочных средних к нормальной кривой. Это дает возможность опираться на законы вероятностей и прогнозировать надежность выборочных наблюдений.
При идеальном случайном отборе в пределах одного среднего квадратического отклонения варьируют результаты 68,27% всех возможных выборок, в пределах двух средних квадратических отклонений — 95,45%, а в пределах трех «сигм» — 99,73%.
Это означает, что при достаточно большом числе замеров в среднем из каждых 1000 выборок 683 дадут значения, не выходящие за пределы одной «сигмы», 954 не выйдут за пределы двух «сигм», а 997 — за пределы трех «сигм». Это означает также, что при любой выборке есть риск ошибиться. В среднем лишь в трех выборках из 1000 ошибка будет больше заданных значений. Увеличим точность приближения к средней всех выборочных средних до двух «сигм», и риск ошибиться возрастет до 46 случаев из 1000; за пределы одного среднего квадратического отклонения выйдут 317 выборок из 1000 (рис. 5.2).
«Правило трех сигм» позволяет заранее оценить вероятность ошибки случайной выборки. Чем выше требования к точности, тем выше риск ошибки и соответственно ниже вероятность правильного ответа. Вообще, выборка аналогична стрельбе в цель: чем больше по размеру мишень, тем выше вероятность попадания. Если сделать 1000 выстрелов из оружия, прицел которого установлен правильно, 683 выстрела будут удачными в том смысле, что не выйдут за пределы одной «сигмы».
«Правило трех сигм» действует применительно к случайным процессам — выпадениям правильного «кубика», монетки, шарам. Но мы знаем, что и вариация выборочной средней является случайным процессом: средняя всех выборочных средних в точности равна генеральной средней, а среднее квадратическое отклонение тоже известно. Поэтому в любом ряду распределения можно установить пределы, в которых находятся выборочные средние с вероятностью 683 из 1000; 954 из 1000 и 997 из 1000.
Вернемся к условному примеру, где производилась выборка из двух человек в генеральной совокупности из пяти человек. Средние затраты времени на чтение составили в 25 выборках 40 мин. Среднее квадратическое отклонение 17,3 мин. Сейчас мы можем подсчитать область распределения, соответствующую одному среднему квадратическому отклонению: нижний предел 40 мин. — 17,3 мин = 22,7 мин;
12*
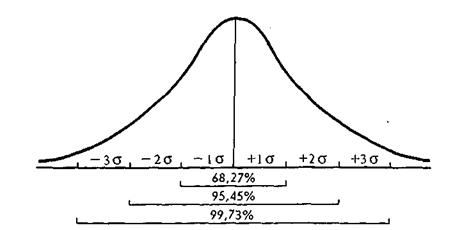
Рис. 5.2. Распределение выборочных средних
верхний предел 40 мин + 17,3 мин = 57,3 мин. Какие из 25 выборочных средних попадают в этот интервал? Посмотрим табл. 5.11 и увидим, что в интервале от 22,7 мин до 57,3 мин имеются значения 25 мин — две выборки, 30 мин —четыре выборки, 35 мин — две выборки, 40 мин — одна выборка, 45 мин — четыре выборки и 50 мин — три выборки. Общей сложностью насчитывается 16 выборок из 25 (2+4+2+1+4+3). Переведем эту цифру в проценты и получим 64 — такова вероятность, что наша случайная выборка не выйдет за пределы одного среднего квадратического отклонения. Расхождение с одной «сигмой» обусловлено малочисленностью наблюдений.
Удвоенное среднее квадратическое отклонение равно 17,3 х 2 = 34,6 мин. Нижняя граница интервала составляет в данном случае 40 — 34,6 = 5,4 мин; верхняя граница: 40 + 34,6 = 74,6 мин. Из всех наших выборок только одна (80 мин.) вышла из этих пределов, а 24 уместились в две «сигмы». В нормальном распределении данный интервал включает 95,4% выборок. У нас таких 96%. Утроенное среднее отклонение охватит в нашем условном примере все выборочные средние. В реальности же три из 1000 случайных выборок выйдут за пределы «трех сигм».
Производя выборку, исследователь не имеет возможности установить ее среднее квадратическое отклонение—для этого понадобилось бы анализировать все выборочные средние. Приходится использовать установленное теорией соотношение между средним квадратическим отклонением выборочных средних и средним квадратическим откло
нением генеральной совокупности 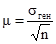 где п — объем выборки.
где п — объем выборки.
Очевидно, чем больше объем выборки, тем меньше вариация выборочных средних.
Проверим это соотношение на нашем условном примере: установим среднее квадратическое отклонение затрат времени на чтение у пяти человек (табл.5. 13).
Таблица 5.13
Дата добавления: 2016-10-17; просмотров: 697;
