Условно-разделительные умозаключения

Ограничимся рассмотрением некоторых условно-раздели-тельных умозаключений,а именно,дилемм, в составе которых содержится две условные посылки, а третья – разделительная. Пример таких умозаключений, называемых конструктивной дилеммой:

1. Если N. похитил чужое имущество, то он должен быть привлечен к уголовной ответственности.

2. Если N. самовольно привел его в негодность, то и в этом случае он должен быть привлечен к уголовной ответственности.

3. N. похитил чужое имущество или самовольно привел его в негодность.

4. N. должен быть привлечен к уголовной ответственности.

Логическая схема этого умозаключения такова:

1. Если р , то q

2. Если r, то q

3. р или r

4. q

Рассмотрим теперь пример умозаключений, именуемых деструктивной дилеммой:

1. Если N. автор этого слуха, то он беспринципен.

2. Если N. автор этого слуха, то он глуп.

3. N. не беспринципен или не глуп.

4. N. не является автором этого слуха.

Логическая схема этого умозаключения такова:

1. Если р , то q

2. Если р, то r

3. не - q или не - r

4. не- р

* * *

Теоретически схем правильных дедуктивных выводов из сложных суждений бесконечно много. Некоторые из них, рассмотренные выше, попадают в учебники по логике по той причине, что они часто используются в практике мышления (в дальнейшем мы пополним их список). Современная логика разработала системы с небольшим количеством довольно несложных и интуитивно приемлемых правил, с помощью которых можно установить правильность (или, напротив, неправильность) любых схем дедуктивных выводов из сложных суждений.

Практикум

1. Установите, какие из приведенных ниже умозаключений имеют дедуктивный характер. Обоснуйте свой ответ.

а) Если преступление совершил Джон, то он знает, с помощью какого оружия оно совершено. Однако Джон не знает этого. Значит, Джон не совершал этого преступления.

б) Если не пойдут дожди, то грибов не будет. Дожди не пошли. Следовательно, грибов не будет.

в) Если человек знает законы, он поступает правильно. Смит не знает законов, поэтому он не поступает правильно.

г) Если подсудимый признается судом виновным в совершении преступления, то он подлежит уголовной ответственности. N. признан судом виновным в совершении преступления. Следовательно, N. подлежит уголовной ответственности.

2. Используя условную (импликативную) посылку и добавив (самостоятельно) еще одну (недостающую), постройте условно-категорическое умозаключение: по утверждающему модусу (правило МП); по отрицающему модусу (правило МТ). Составьте формальные схемы полученных выводов.

а) Если цветы не поливают, они вянут.

б) Если дожди не прекратятся, река выйдет из берегов.

в) Если он не знает логику, то не сможет решить эту задачу.

г) Когда в товарищах согласья нет, на лад их дело не пойдет.

д) Если бухта замерзает, суда не могут входить в бухту.

3. Установите корректность следующих чисто-условных выводов:

а) Если больному сделать операцию, то он поправится. Поправившись, он вернется на работу. Значит, если больному сделать операцию, он вернется на работу.

б) Если студент не занимается систематически, то он не имеет прочных знаний. Когда у студента прочные знания, из него получается хороший специалист. Следовательно, если студент не занимается систематически, то из него не выйдет хорошего специалиста.

в) Если человек трус, он не протестует против незаконного обращения. Значит, если человек протестует против незаконного обращения, он не является трусом.

г) Когда у меня болит зуб, я принимаю анальгин. Следовательно, если у меня не болит зуб, я не принимаю анальгин.

4. Используя разделительную (дизъюнктивную) посылку и добавив (самостоятельно) недостающую, постройте разделительно-катего-рическое умозаключение: а) по утверждающему модусу (правилоИД₂);
б) по отрицающему модусу (правилоИД₁).

1) Обвиняемый N. может быть исполнителем либо организатором преступного деяния. 2) Подпись на расписке могла быть выполнена N., или М., или К. 3) Наш попутчик мог выйти только на одной из двух промежуточных остановок, где останавливался поезд: Боброво либо Озерная.

5. Обоснуйте дедуктивный характер следующих умозаключений:

а) Если цены возрастут, то политическая ситуация обострится, а если не возрастут, увеличится дефицит. Правительство не допустило обострения политической ситуации. Значит, увеличится дефицит.

б) Если исход скачек предрешен сговором, то доходы от туризма в городе падают. Если доходы от туризма падают, то этим полиция недовольна. Но полиция довольна. Значит, исход скачек не предрешен
сговором.

6. Проанализируйте следующие умозаключения (проверьте корректность, а в некоторых из них сформулируйте заключение):

1) Договор будет заключен, если между договаривающимися сторонами будет достигнуто соглашение. Но договор заключен не будет, поскольку между сторонами не было достигнуто соглашение.

2) Наполеон укреплял свою власть или заботился об интересах государства. Наполеон заботился об интересах государства. Следовательно, он не укреплял свою власть.

6) Обвиняемый может быть либо исполнителем, либо организатором, либо подстрекателем, либо пособником. Обвиняемый N. является организатором совершенного преступления. Следовательно?...

4.2.3. Дедуктивные выводы
из категорических суждений

Приступаем к рассмотрению дедуктивных умозаключений, основанных на внутренней структуре (логической форме) категорических суждений. Рассмотрим первый пример таких умозаключений:

1. Некоторые депутаты областной думы – юристы.

2. Некоторые юристы – депутаты областной думы.

Очевидно, что если истинно суждение над чертой, то обязательно истинно суждение под чертой (черта, как и ранее, означает «следовательно»). Так будет и в том случае, если вместо фигурирующих в этом умозаключении понятий (терминов) «депутат областной думы» и «юрист» поставить понятия «студент» и «спортсмен», или «водоплавающие» и «млекопитающие» и т.п. Заменив в этом умозаключении термины на логические переменные S и Р, получим одну из схем (логическую форму) дедуктивного вывода:

SiР

РiS

В этой схеме выражение SiР является сокращенной записью логической формы частноутвердительного суждения «Некоторые S суть Р», а
Рi S – логической формы частноутвердительного суждения «Некоторые Р суть S». (Аналогичные сокращения были приняты и для других категорических суждений). В соответствии с данной схемой осуществляются и такие однопосылочные умозаключения: Некоторые студенты – спортсмены, следовательно, некоторые спортсмены – студенты; Некоторые водоплавающие – млекопитающие, значит, некоторые млекопитающие – водоплавающие.

Рассмотрим второй пример, в котором не одна, а две посылки:

1. Все депутаты областной думы – политические

деятели.

2. Некоторые юристы – депутаты областной думы.

3. Некоторые юристы – политические деятели.

Заменив термины этого умозаключения «депутат областной думы», «политический деятель» и «юрист» на логические переменные М, Р и S, получаем схему (логическую форму) дедуктивного вывода

МаР

SiM

SiP

Данная схема составляет логическую основу и таких двухпосылочных умозаключений: Все спортсмены ведут здоровый образ жизни. Некоторые студенты – спортсмены. Следовательно, некоторые студенты ведут здоровый образ жизни .·. Все млекопитающие – теплокровны. Некоторые водоплавающие – млекопитающие. Следовательно, некоторые водоплавающие – теплокровные.

Все выводы из категорических суждений делят на два вида: непосредственные и опосредованные. В непосредственных умозаключениях только одна посылка, в опосредованных – две (и более). Рассмотрим в этом разделе однопосылочные выводы из категорических суждений.

4.2.3.1. Выводы по логическому «квадрату»

Эти умозаключения основаны на логических отношениях между категорическими суждениями, иллюстрируемых известным нам логическим «квадратом» (раздел 3.3). Напомним, что логические отношения не зависят от конкретного содержания суждений, поэтому в дальнейшем эти отношения будут рассматриваться как связи между логическими формами (формулами) суждений. Одно из них – контрарность, или противоположность, имеет место между общеутвердительным и общеотрицательным суждениями (a 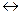e). Этот тип отношений характеризуется следующей логической необходимостью: при истинности суждения SаP суждение SeP будет с необходимостью ложным, и наоборот. Поэтому, зная, что Любая кража есть уголовное преступление, заключаем: Неверно, что ни одна кража не является уголовным преступлением. Действительно, при истинности суждения SаР контрарное ему суждение SеР будет обязательно ложным, а его отрицание – истинным. Далее, зная, что Ни один кит не дышит жабрами, заключаем: Неверно, что все киты дышат жабрами. И в том, и в другом случае истинность посылки гарантирует истинность заключения. Остальные два варианта распределения значений истинности контрарных суждений такой логической необходимости не дают.

Рассмотрим разновидности умозаключений, логическим основанием которых является отношение контрадикторности, или противоречия (они называются диагональными). Оно имеет место между общеутвердительным и частноотрицательным суждениями, а также между общеотрицательным и частноутвердительным суждениями(a 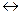o, e 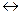i). При истинности SaP будет с логической необходимостью ложным SoP, и наоборот; при истинности SeP будет с необходимостью ложным SiP, и наоборот. Поэтому, зная, к примеру, что Любая кража есть уголовное преступление, заключаем: «Неверно, что некоторые кражи не являются уголовным преступлением». Аналогично, зная, что Некоторые металлы не являются твердыми веществами, заключаем: «Неверно, что все металлы – твердые вещества».

Отношение логического подчинения (а 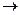i, e 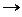о) характеризуется следующей необходимостью: при истинности SaP будет с необходимостью истинно SiP, а при истинности SeP истинным будет SoP. Поэтому зная, что Все свидетели по данному делу прибыли на судебное заседание, заключаем,чтои Некоторые свидетели по данному делу прибыли на судебное заседание. Аналогично, корректным будет переход от посылки Ни один кит не дышит жабрами к заключению Некоторые киты не дышат жабрами.

Осуществляя выводы по логическому квадрату, полезно помнить:

*Если признается истинность общего суждения (SаР либо SеР), то имеется возможность однозначно заключить о ложности либо истинности всех других суждений логического квадрата.

*Признание ложности частного суждения (SiР либо SоР) позволяет однозначно заключить об истинности либо ложности всех других.

4.2.3.2. Обращение

Обращение – это умозаключение, при котором из данного суждения, не являющегося частноотрицательным, выводимо другое суждение, субъектом которого является предикат посылки, а предикатом – субъект посылки. Качество заключения остается тем же, что и у посылки. Что касается количества, то оно может изменяться. Все зависит от распределенности терминов: если термин был распределен в посылке, он может быть
распределен и в заключении; если же термин не распределен в посылке,
не может быть распределен в заключении. Сформулируем правила (схемы) обращения:

Правило простого обращения суждений типа SеР:

Если истинна посылка «Все S не суть Р», то истинно и заключение «Все Р не суть S». Правильность этой разновидности непосредственного вывода хорошо видна на схеме отношений терминов S и Р в посылке и заключении:

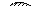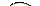Приведем пример умозаключения, построенного на использовании данного правила:

1. Ни один равнодушный человек не является добрым

2. Ни один добрый человек не является равнодушным

В исходном суждении (посылке 1.) субъектом S является понятие «равнодушный человек», а предикатом Р – понятие «добрый» (человек). Заключение 2. является конверсией (обращением) посылки 1.: что было субъектом, стало предикатом, а то, что было предикатом, стало субъектом.

Правило простого обращения суждений типа SiР:

Если истинна посылка «Некоторые S суть Р», то истинно и заключение «Некоторые Р суть S»:

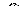
Пример:

1. Некоторые добрые люди – адвокаты

2. Некоторые адвокаты – добрые люди

Правило ограниченного обращения суждений типа S аР:

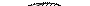
Пример:

1. Все адвокаты – образованные люди

2. Некоторые образованные люди – адвокаты

Из схемы видно, что более сильное утверждение Все образованные люди – адвокаты в качестве заключения рассматриваемого умозаключения было бы ошибочным. Отсюда и добавление к названию правила – ограниченное обращение.

Суждения типа SоР не могут быть обращены, поскольку, к примеру, из истинного суждения Некоторые люди не знают математики по этому методу выводится ложное суждение Некоторые из тех, кто знает математику, не являются людьми.

4.2.3.3. Превращение

Представляет собой вывод, в котором заключение получается из посылки посредством постановки на место предиката исходного суждения такого понятия, которое находится в отношении противоречия к этому предикату (было положительным, становится отрицательным, и наоборот), и при этом изменяется на противоположное качество суждения (положительное становится отрицательным, и наоборот). Сформулируем правила превращения:

Правило превращения суждений типа SаР:

Если истинна посылка «Все S суть Р», то истинно и заключение «Все S не суть не-Р».Пример:

1. Все жидкости – упруги

2. Ни одна жидкость не является неупругим веществом

Правило превращения суждений типа SеР:

Если истинна посылка «Все S не суть Р», то истинно и заключение «Все S суть не-Р». Пример:

1. Ни один интеллигент не является злодеем

2. Все интеллигенты – незлодеи

Правило превращения суждений типа SiР:

Если истинна посылка «Некоторые S суть Р», то истинным будет и заключение «Некоторые S не суть не-Р». Пример:

1. Некоторые студенты – спортсмены

2. Некоторые студенты не являются неспортсменами

Правило превращения суждений типа SоР:

Если истинна посылка «Некоторые S не суть Р», то истинно и заключение «Некоторые S суть не-Р».Пример:

1. Некоторые студенты не являются самолюбивыми

2. Некоторые студенты являются несамолюбивыми

Практикум

1. Осуществите возможные дедуктивные выводы по логическому квадрату из следующих суждений:

а) Все студенты сдают экзамены. б) Не каждый студент сдает их успешно. в) Некоторые студенты волнуются при сдаче экзамена. г) Ни один студент не освобождается от сдачи экзаменов. Некоторые ученые работают в вузе. б) Некоторые ученые не работают в вузе.

*Пример. Некоторые металлы не окисляются. Данная посылка – частноотрицательное суждение. Если оно истинно, то можно заключить о ложности противоречащего ему общеутвердительного суждения. О значениях же общеотрицательного и частноутвердительного суждений ничего определенного сказать нельзя. Поэтому единственно возможное заключение из данного суждения: Неверно, что все металлы окисляются.

2. Какое из нижеприведенных суждений не подлежит обращению?

в) Ни один человек не желает себе зла. г) Все люди – братья.

3. Постройте выводы посредством превращения следующих суждений:

а) Некоторые юристы – адвокаты; б) Все адвокаты – юристы; в) Некоторые простые решения не являются эффективными.