Приемы работы при изучении системы счисления

Аналогичное положение существует и при изучении математики. Уже указывалось, что начальный курс математики может быть изучен быстрее и глубже, если он построен в соответствии с современными психологическими знаниями о возрастных возможностях детей, а также с учетом законов процесса усвоения.

Остановимся на начальных умениях, определяющих успех учащихся в овладении системой счисления.

Прежде всего отметим, что при изучении и этого предмета должна быть выделена основная (фундаментальная) система знаний и умений, которая и определяет успех начального математического образования.

В качестве примера рассмотрим экспериментальную программу, разработанную в Московском университете Н.Г. Салминой и В.П. Сохиной под руководством П.Я. Гальперина.

Одним из основных понятий этой программы является понятие меры, а одним из основных действий - измерение.

Если при обучении чтению до введения букв тщательно отрабатывается действие звукового анализа, то в курсе математики до введения чисел учащиеся усваивают измерение с использованием различного рода мер: простых и составных, больших и малых, для измерения дискретных и непрерывных величин.

Для обозначения результата измерения используются мет­ки (фишки, пуговки и т.п.).

Важным понятием является понятие величины. Выделение величин, подлежащих измерению, требует от детей умения выделять разные свойства в объектах. Вот почему изучение математики необходимо начинать с формирования этого ло­гического приема, если дети им не владеют.

Другое важное понятие, которое необходимо для овладе­ния действием измерения, - понятие о соответствии меры измеряемой величине (объем измеряется объемом, масса - мас­сой, протяженность - мерами протяженности, площадь - площадью и т.д.). В необходимости соблюдения этого требо­вания дети убеждаются практически: им предлагают, напри­мер, измерить кружку веревочкой. Аналогичным образом дети убеждаются и в необходимости меток. Им предлагается, например, измерить длину края стола (парты) с помощью счетной палочки. Работая без меток, дети не могут сказать, сколько раз уложилась мера в измеряемой величине. Посте­пенно, показывая практически необходимость выполнения целого ряда требований при измерении, учитель формулирует вместе с детьми правила измерения:

1. Выбор величины, которая будет измеряться.

2. Выбор меры для измерения.

3. Правило работы с мерой:

а) при измерении протяженности выбор точки, от ко­торой начинается измерение;

б) обозначение конечной точки каждого отмеривания;

в) в случае сыпучих тел - насыпание до краев.

4. Выкладывание метки после каждого измерения. (Если при последнем измерении мера не укладывается полностью - остается остаток.)

При выполнении каждого измерения учащиеся производят не только практические измерения, но и обязательно прого­варивают, с чего они будут начинать измерение, как его будут производить, фиксировать его результат и т.д.

После освоения действия измерения учащиеся усваивают действие сравнения двух величин. Здесь учащиеся осваивают действие установления взаимно-однозначного соответствия между двумя множествами. Необходимо показать, что срав­нивать величины можно только в том случае, когда они измерены одной и той же мерой. Предлагается, например, сравнить по объему две чашки крупы, которые резко различаются по величине. При этом крупу в маленькой чашке надо измерить маленькими чайными ложками, а в большой - большими столовыми. Дети получают два ряда меток, приводят их во взаимно-однозначное соответствие и видят: по меткам оказывается, что в маленькой чашечке крупы больше. Но очевидно, что это не так. И вот тут выясняется, почему получен неверный результат.

Можно использовать и такие величины (например, длину ленточек), которые не равны, а измерение разными мерами одно и то же число меток, т.е. получается, что ленточки одинаковой длины, а на самом деле они разные по длине. Ошибка очевидна. В дальнейшем это условие выполняется детьми очень строго.

Формирование понятий равно, не равно, больше, меньше идет успешней, если учитель предлагает не абстрактные задачи, не скучные отрезки и площади сами по себе, а облекает их в задачи, интересные для детей шести-семи лет. Например, учитель предлагает сравнить по длине дорожки, по которым бегают зверьки к ручейку пить. Дети могут разоблачить с помощью измерения хитрую лису, которая нечестно делила крупу с медведем и т. д.

Результат каждого сравнения, производимого детьми практически, руками, предстает перед ними в наглядном виде. Так, например, сравнивая по длине дорожки ежика и мышки, дети поучили такой результат:

Е

М

Очевидно, что дорожка ежика длиннее на три мерочки. Постепенно дети учатся записывать полученные результаты на математическом языке («переводят» на математический язык), употребляя буквы и математические знаки, отношения между двумя множествами (=, =, >, <).

Учащиеся сами получают последовательный ряд чисел, используя один и тот же способ: прибавление одной единицы к полученному числу. После введений чисел в пределах 10 учащиеся знакомятся с арифметическими действиями, с переместительным и сочетательным законами и на этой основе дета­льно изучают состав числа, раскладывая его на различные группы единиц. Большое внимание уделяется счету равными группами, что является подготовкой к введению умножения. Работа идет с использованием числовой оси. Для детей такой счет выступает как переход на более крупную меру.

Необходимость умножения доказывается учащимся через решение соответствующих задач. Например, предлагается узнать, сколько птичек можно накормить крупой, которая содержится в пакете. Каждой птичке нужна одна чайная ложка крупы.

Учащимся предлагается найти способы решения задачи. Ра­бота чайными ложками отвергается как длительная. Столовые ложки дают сравнительно быстро результат, но ответ на во­прос задачи остается не полученным. Обязательно кто-то из детей догадается: «Надо измерить, сколько чайных ложек вой­дет в столовую». Измеряют. Допустим, входят две ложки.

ст. л. ст. л.

Дети логично воспринимают умножение как изменение меры: брали сразу по две чайных ложки. И, допустим, брали такой мерой пять раз. Отсюда появляется запись 2х5=10.

Работали мелкими мерами (чайные ложки), но брали сразу по две таких меры.

Деление вводится как действие, обратное умножению: пере­ход на укрупненную меру. Допустим, есть 10 ложек крупы. На­до узнать, на сколько птичек хватит этой крупы, если каждая птичка съедает по две ложки. И надо знать, сколько раз содер­жится эта новая мера в измеряемом. Как видим, на основе меры и действия измерения можно показать детям и число, и дейст­вия с ним. Эти же понятия позволяют раскрыть перед учащи­мися различные системы счисления и позиционный принцип их построения. Каждый новый разряд системы счисления рас­сматривается как новая мера счета, а соотношения разрядов как соотношения мер, каждая из которых в определенное чис­ло раз больше, чем мера предыдущего разряда.Так, в деся­тичной системе 10 единиц первого разряда (единиц) дают единицу второго разряда (десятки) и т.д. Учащиеся сами об­разуют новые «меры счета», работая с разрядной сеткой.

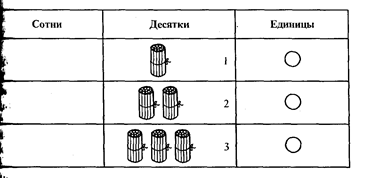
Так, единицы любого разряда считаются и записываются одинаково, поэтому дети легко начинают выполнять все арифметические действия с единицами любого разряда.

Позднее меры используются также при изучении десятичных и обыкновенных дробей. Следует отметить, что при таком подходе к построению курса начальной математики логичней вводить вначале десятичные дроби, а потом уже обыкновенные. Десятичные дроби выступают как вторая часть системы счисления, где мера при переходе от разряда в разряд не увеличивается, а наоборот, уменьшается. Обыкновенные дроби выступают перед учащимися тоже как переход на новую меру измере­ния, но теперь мера уменьшается не в десять, а в какое-то другое число раз. Характерно, что учащиеся, работающие по данным программам, никогда не допускают таких распространенных в школе ошибок при сложении дробей, как выполнение этого действия отдельно вначале на числителях, а затем - на знаменателях.

Работая с мерами, учащиеся с самого начала усваивают, что складывать и вычитать можно только измеренное одной и той же мерой. Поэтому, чтобы сложить 1/4 и 1/6, необходимо привести их к общей мере - к общему знаменателю.

Отметим, что многолетний опыт работы по данной программе показал, что принципы ее построения позволяют учащимся глубоко проникнуть в основы систем счисления, легко переходить из одной системы в другую. Одновременно это дает серьезное сокращение времени, необходимое для усвоения начального курса математики. Наконец, учет закономерностей усвоения и возрастных особенностей детей при разработке методики обучения позволяет обеспечить полноценное усвоение данного курса всеми учащимися.

Аналогичный подход - через выделение основополагающих понятий и действий - следует реализовать применительно и к умениям, обеспечивающим решение задач.

11.4. Прием решения арифметических задач «на процессы»

Прежде всего отметим, что ориентировочная основа дей­ствий, составляющих умение решать эти задачи, лежит вне арифметики: для того, чтобы описать математическим языком ситуацию, приведенную в условии задачи, необходимо выде­лить в этой ситуации основные элементы и их отношения.

Все эти задачи основаны на одних и тех же понятиях: ско­рость, время и результат («продукт») процесса, к которому процесс приводит или который он уничтожает.

В силу этого учащимся можно дать общий прием решения всех арифметических задач на процессы, построить его ориен­тировочную основу по третьему типу. Ориентировочная ос­нова умения решать задачи «на процессы» включает в себя понятия: скорость, время, продукт процесса.

Для успешного решения задач данного типа необходимо также понимать отношения между основными элементами ситуации: а) величина продукта прямо пропорциональна ско­рости и времени; б) время, необходимое для получения про­дукта, прямо пропорционально величине продукта и обратно пропорционально скорости и т.д. Далее важно усвоить, что по двум из этих элементов всегда можно найти третий, если речь идет об одном участнике процесса (об одной действую­щей силе). В самом деле, S = Vx Т; V = S : Т; Т = S : V. Нако­нец, если продукт создают несколько участников, то в этом случае появляется новая система отношений - отношения между частными и общими значениями по каждому парамет­ру, определяемые характером участия отдельных сил: помо­гают участники друг другу или противодействуют, одновре­менно или разновременно участвуют в процессе и т.д. В дан­ном случае общая скорость, например, может иметь следую­щее выражение: V₀ = V₁ + V₂ (если участники помогают друг другу); V₀ = V₁ – V₂ (если участники противодействуют) и т.д.

Все это входит в состав данного умения и составляет про­грамму того, чему в данном случае следует учить. Только после усвоения всех основных элементов и их отношений может быть дан общий метод анализа, позволяющий устанавливать систему отношений в условиях любой конкретной задачи данного типа.

Прежде всего у обучаемых надо сформировать систему по­нятий: время, скорость, продукт процесса. Проверка показы­вает, что обычно учащиеся не владеют ни этими понятиями, ни отношениями между ними. Так, например, у многих уча­щихся не отдифференцировано даже время как определенный временной момент (точка отсчета) и время как некоторый временной интервал. (Если, например, в задаче говорится, что поезд отправился в 10 часов утра, учащиеся считают, что время его движения равно 10 часам.)

Формирование основных понятий - время процесса, скорость процесса и продукт процесса - завершается усвоением их отношений; учащиеся учатся находить любой из трех ука­зных элементов по двум остальным. Формирование всех элементов должно осуществляться с поэтапной отработкой. На этапе материализованного действия широко используются пространственные схемы, модели. Так, например, скорость, продукт процесса изображаются в виде отрезка прямой, время - в виде отрезка, разделенного на соответствующее число частей. Учащемуся предлагается, допустим, получить продукт процесса по данной ему скорости и времени. Он получает его, откладывая отрезок, моделирующий скорость, столько раз, сколько частей содержит другой отрезок, моделирующий время. Это практическое действие учащийся без труда заканчивает математическим описанием, так как он только что получил продукт путем последовательного прибавления одной и той же величины, т.е. одно и то же брал определенное число раз. Поэтому ученик без труда записывает это как скорость, умноженную на время. Таким образом, исполнитель­ные операции ученик может определять самостоятельно. Аналогично на этом этапе проходит усвоение и всех остальных компонентов умения.

После этого испытуемых надо учить выделять элементы в ситуации, описанной словами, анализировать условия задач по данному им плану. Это уже внешнеречевой уровень усвое­ния. План анализа имеет примерно такой вид:

1. Кто действует (F)?

2. Что получается в результате его действия (S)?

3. Сколько времени происходит действие (Т)?

4. Сколько выполняет за одну единицу времени (V)?

Учащихся учат находить в условии задачи данные, содержащие ответ на каждый из пунктов предписания, подчеркивать эту часть условия определенной линией и ставить под ней (или над ней) соответствующий символ (F, V, Т, S). После этого учащиеся записывают условие задачи с помощью сим­волов, проставляя против каждого из них конкретные данные или ставя знак вопроса, если величина неизвестна.

Вот как выглядела одна из задач после анализа ее усло­вий: «Три машины израсходовали за 10 часов (Т₀) 250 л го­рючего (S₀). Известно, что за это время первая машина израсходовала 60 л (S₁,), а вторая - 110 л (S₂) Найдите, сколько расходовала третья машина за час (V₃)?»

И только после усвоения учащимися данной формы анали­за следует учить их анализировать условие задачи про себя.

Вслед за усвоением всех выделенных элементов, их отно­шений и общего метода анализа условий задачи учащимся надо дать метод составления схемы ситуации и плана реше­ния. Вначале это делается применительно к одному участнику, а затем - в условиях совместного действия, где участники процесса могут как помогать, так и мешать друг другу. Те­перь дается уже общее предписание, позволяющее проанали­зировать условие задачи, составить схему ситуации и план решения. Предписание предлагает выделить в условии задачи участников процесса, то, как они действуют (помогают или противодействуют), время участия каждого из них и т.д. В ре­зультате такого анализа появляется запись условий задачи в определенной системе символов. Запись данных:

T₀=10ч

S₀= 250 л

S₁ =60 л

S₂= 110л

V₃=?

После этого ученику предлагается выделить искомое, обозначить его соответствующим символом (V, S, Т, V₂, T₂, S₂, и т.д.) и обвести кружком из пунктирной линии (знак неиз­вестного). В вышеприведенной задаче искомым является ско­рость третьего участника процесса (V₃). Затем предлагается указать величины, с помощью которых ее можно получить. Ученик после усвоения основных элементов и их отношений знает, что она может быть получена только двумя путями: или через время (T) и продукт (S), относящиеся к третьему участ­нику, или через общую скорость и скорости отдельных участ­ников. И он изображает следующее:

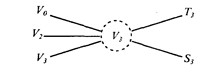
Затем предписание предлагает обозначить, какие из ука­занных элементов известны, какие нет; учащийся анализирует условие задачи дальше и устанавливает, что T₃ есть, а S₃ - нет и т.д. Тогда схема приобретает такой вид (сплошная линия - знак известного).

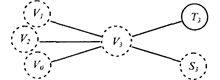
Теперь учащийся должен установить, как можно найти V₃. Он знает, что V₃ можно найти двумя путями: через T₃ и через S₃ или через V₀ и частные V₁ и V₂. Продолжая по предписанию анализ данных задачи, ученик получает такую схему:

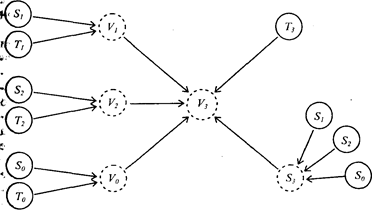
Из схемы видно, что путь, намеченный и справа, и слева, приводит к решению. Но путь справа короче.

На основе схемы ситуации учащиеся составляют план решения задачи и реализуют его. Исполнительные операции никакого труда для учащихся не представляют, так как они уже усвоили математическое выражение тех отношений, которые существуют между изображенными элементами ситуации.

Проверка программы показала, что при таком обучении даже самые слабые ученики третьего класса усваивают об­щий прием решения задач на процессы и успешно применя­ют его. Обучение обычно занимает 11-12 уроков, т.е. гораз­до меньше, чем обычно тратится на усвоение всех разновид­ностей задач этого типа при школьном обучении. Этот при­ем мы рассмотрели в материализованной форме; обобщение - в пределах всех видов школьных задач на процессы. Решая задачи данного класса, учащиеся постепенно перейдут на умственный этап. Читая условие задачи, они уже не будут выделять отдельные элементы знаками; постепенно не будут выписывать данные, не будут составлять и схему решения: все это они будут делать про себя, быстро, и как бы сразу видеть рациональный путь решения.

Как видим, при составлении программы для формирова­ния умения решать арифметические задачи также необходимо прежде всего выделить основные понятия, на которые опира­ются задачи и которые (в данном случае это понятие скоро­сти, времени, продукта, действующих сил) составляют специ­фику задач данного класса, затем выделить отношения между этими понятиями и на этой основе дать общий метод анализа задач данного класса. Разумеется, общий метод анализа также должен пройти поэтапную отработку. В конечном итоге он может применяться без опоры на схему.

Преимущество схематизации ситуации, данной в условии задачи, состоит в том, что текст «переводится» на язык на­глядной и в то же время абстрактной модели, где все отноше­ния ситуации выступают перед учеником одновременно. Кро­ме того, на схеме представлен и план решения: количество элементов, обведенных кружками из пунктирной линии, пока­зывает, во сколько вопросов (и действий) может быть решена задача. Направление стрелок показывает, в каком порядке при этом следует действовать.

Особенность этой схемы состоит в том, что содержание исполнительных действий на ней не представлено. Она моде­лирует лишь специфические элементы ситуации и их отноше­ния, т.е. ориентировочную основу действия. Но, как показали исследования, после специальной отработки основных эле­ментов (Т, V, S ) и их отношений исполнительные операции не представляют труда даже при решении сложных задач, так как они те же самые. Трудность решения этих задач не в арифметических действиях самих по себе, а в адекватности их применения. Рассмотренный прием дает возможность ученику при решении всех задач данного типа составить полную ори­ентировочную основу, что обеспечивает понимание заданной системы отношений и, следовательно, адекватный перевод их на язык арифметических действий.

Логика исполнительных действий определяется логикой ситуации, представленной в условии задачи. При обучении решению арифметических задач учитель должен раскрыть ученику эти отношения, сформировать у него полную и адек­ватную ориентировочную основу выполняемых действий.

Преимущество такого пути обучения доказывают резуль­таты сравнительной и контрольной серий опытов. После обучения 18 испытуемым были даны две усложненные задачи. Вот одна из них: «Надо посадить 60 деревьев. Если будет работать только третий класс, то работа будет выполнена за 3 часа; если будет работать только четвертый класс, то работа будет выполнена за 6 часов. За сколько времени будет выполнена работа, если оба класса будут работать вместе?»

Одна из них была решена всеми испытуемыми вполне самостоятельно. При решении второй, приведенной здесь задачи, семи испытуемым потребовалась небольшая помощь экспериментатора. Затруднения были вызваны условной формой представления данных, что и привело к тому, что не все ученики сумели понять их. Если даже признать эти семь решений ошибочными, то и в этом случае правильные решения составляют 81 %.

Эти же задачи были даны 72 среднеуспевающим учащимся четвертых, пятых, шестых и восьмых классов (18 человек из каждого класса). Оказалось, что правильные решения составили лишь 22% в четвертом классе, 33% в пятом классе, 50% в шестом классе и 19% в восьмом классе. Учащимся шестых и восьмых классов, не справившимся с задачами, было разре­шено пользоваться алгебраическими способами решения, но и это не помогло.

Как видим, результаты плохие. Особенно показательны низкие результаты учащихся восьмых классов: изучение алгебры после изучения арифметики привело не к обобщению арифметических способов решения, не к пониманию их как частных случаев алгебраических отношений, а к забыванию в том виде, в каком они были усвоены.

Преимущество обучения, направленного на формирование прежде всего ориентировочной основы действий, состоит в том, что оно, обеспечивая понимание, сознательный выбор исполнительных действий, делает учащихся самостоятельными, создает у них положительное отношение к занятиям. Из­менение отношения учащихся к арифметике происходит бук­вально на глазах. Вначале учащиеся занимались неохотно (занятия шли за счет их свободного времени), они не скрывали своего отрицательного отношения к решению задач. Но буквально через два-три занятия положение изменилось: дети старались как можно больше решить задач на занятиях, чаще заниматься, исчезла невнимательность. После решения учащимися контрольных задач им было объявлено, что фор­ма занятий меняется: кто хочет - должен сам искать задачи в учебниках арифметики, решать их, а экспериментатору при­носить решения для проверки. Оказалось, что все учащиеся это стали делать, хотя их никто к этому не обязывал, за это не ставили никаких оценок и никто не напоминал им об этом. Учащимися руководил только непосредственный интерес к решению задач, которые стали теперь им доступны'.

' Подробное изложение методики работы с задачами данного типа см.: Никола Г., Талызина Н.Ф. Формирование общих приемов решения арифметических задач // Формирование приемов математического мыш­ления. - М., 1995.-С. 68-120.

Возможно дальнейшее обобщение рассмотренного приема. Предварительный анализ показал, что задачи на «процессы» и задачи на «куплю-продажу» имеют идентичную систему от­ношений; разница лишь в конкретно-предметном плане, что в данном случае не является существенным. Можно предложить способ анализа, позволяющий учащимся подходить к этим двум большим классам арифметических задач как к разно­видности одного и того же типа.

Контрольные вопросы

1. Назовите несколько действии, необходимых при изучении родного языка.

2. Почему нельзя начинать обучение чтению с букв?

3. Почему сочинение лучше диктанта для овладения языком?

4. Почему решение примеров в арифметике легче, чем решение задач?

5. Какой тип ориентировочной основы действия надо стремиться исполь­зовать при изучении любого предмета? Почему?

7. Назовите действия, которые необходимы учащимся при знакомстве с природой, изобразительным искусством.

Литература

Айдарова Л.И. Психологические проблемы обучения младших школь­ников русскому языку. - М., 1978.

Давыдов В.В. Психологические особенности «дочислового» периода обучения математике // Возрастные возможности усвоения знаний. – М., 1996.-С. 104-189.

Салмина Н.Г., Фореро Навис И. Обучение математике в началь­ной школе. - М., 1995. - С. 29-68.

Никола Г., Талызина Н.Ф. Фомирование общих приемов решения арифметических задач // Формирование приемов математического мышле­ния.-М., 1995.