Начальные логические приемы мышления

Никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учащихся. Об этом говорится в объяснительных записках к учебным программам, об этом пишут в методической литературе для учителей. Однако кон­кретной программы логических приемов мышления, которые должны быть сформированы при изучении данного предмета, пока нет. В результате работа над развитием логического мышления школьников идет «вообще» - без знания системы необходимых приемов, без знания их содержания и последо­вательности формирования. Это приводит к тому, что боль­шинство учащихся не овладевают начальными приемами мышления даже в старших классах школы, а эти приемы не­обходимы уже младшим школьникам: без них не происходит полноценного усвоения материала.

Приведем данные по диагностике логических приемов мышления у учащихся в конце первого года обучения. Прове­рялись три приема: подведение под понятие, выведение след­ствий, сравнение. Все три приема необходимы в первом классе при изучении математики. Оказалось, что только небольшая часть учащихся владеет этими приемами хорошо, у остальных они не сформированы в должной мере.

Больше того, у многих учащихся начальной школы не сформированы и более элементарные логические операции.

Вот посмотрите, как выполняют задания некоторые уча­щиеся второго класса одной из московских школ. Вначале были предъявлены два совершенно равных квадрата, а затем один из них был разрезан по диагонали на два треугольни­ка, из которых, в свою очередь, был составлен один тре­угольник.

Приводим диалог с Андреем П., одним из учеников второ­го класса.

- Андрюша, ты хорошо учишься?

-Да.

- Молодец, скажи, пожалуйста, вот эти фигуры как называются (пока­зываю два квадрата)?

- Квадратики.

- Посмотри, они одинаковые или не одинаковые? Наложи один на дру­гой и хорошо посмотри.

- Одинаковые.

- Одинаковые. Хорошо, значит, квадратики одинаковые, а теперь мы вот этот квадратик разделим на два треугольничка (разрезаю) и из них по­строим один треугольник. А вот теперь скажи, одинаковые по величине эти фигуры: треугольник и квадрат?

- Они не одинаковые.

- А какая больше?

- Вот эта (показывает на треугольник).

- Ты уверен, что эта больше?

-Да.

К сожалению, во втором классе такие ответы не такое редкое явление. Причина ошибки состоит в неумении учени­ка дифференцировать отдельные стороны предметов, в ре­зультате чего изменение одного свойства (формы фигуры) он принимает за изменение другого (площади фигуры), ко­торое в данном случае оставалось неизменным. Такого рода ошибки учащиеся первого-второго классов делают при ра­боте с разными свойствами предметов. Вот, например, как ведет себя один из учеников второго класса в ситуации дру­гой аналогичной задачи. Ученику предъявляются две совер­шенно одинаковые бутылочки с длинными узкими горлыш­ками, наполненные подкрашенной водой до одного и того же уровня.

Между учеником и экспериментатором происходит сле­дующий диалог:

-Саша, скажи, пожалуйста, в бутылочках одинаковое количество жид­кости или неодинаковое?

- Одинаковое.

- Посмотри внимательно, где тебе кажется меньше, где больше?

- Нигде.

- Значит, одинаково?

-Да.

- Хорошо. А теперь посмотри, что я сделаю: возьму вот эту бутылочку и переверну (экспериментатор ставит одну из бутылочек на горлышко). А теперь одинаковое количество жидкости в бутылочках или нет?

-Нет.

- А где меньше, где больше?

- Здесь больше. (Показывает на перевернутую бутылочку).

- Ты уверен в этом, Саша?

-Да.

- А если я опять поставлю бутылочку вот так (экспериментатор ставит бутылочку на донышко). А теперь как?

- Поровну.

- А если я теперь переверну первую бутылочку (первая бутылочка ста­вится на горлышко).

- Здесь (показывает на первую бутылочку).

- Ты уверен?

-Да.

Кажется, так очевидно, что вода никуда не отливалась, и вдруг, по мнению ребенка, ее становится меньше по количест­ву то в одной бутылочке, то в другой. Как и в первом случае, ученик не дифференцирует два свойства: количество жидкости и ее уровень в бутылочке, который меняется при перевертывании последней.

Если эти опыты повторить в первом - втором классах лю­бой другой школы, обязательно найдется значительная группа учеников, которые будут совершать точно такие же ошибки.

В старших классах подобные логические ошибки исчеза­ют, но, к сожалению, сохраняются многие другие. Так, на­пример, простейшие задачи на распознавание объектов, относящихся к понятиям с дизъюнктивной структурой при­знаков (или - или), вызывают затруднения у учащихся вплоть до окончания школы. Вот одна из таких задачек: «Жен­щина подходит к одному из членов вашего коллектива и говорит: «Я тебе мать, а ты мне не дочь». Может быть такая ситуация?» Как правило, учащиеся отвечают, что так быть не может. Иногда начинают придумывать особые ситуации:

«Может, ребенка взяли из детдома» и т.д. Интересно, что ошибки допускают не только девочки, но и мальчики, для которых такая ситуация отражает реальное положение: они не дочери своим матерям.

Особенно большие затруднения вызывает распознавание объектов в задачах с неопределенным составом условий, т.е. когда ответ и не положительный, и не отрицательный, а неоп­ределенный: может, объект относится к данному классу, а может, и нет, так как в условии нет сведений о некоторых свойствах из числа необходимых.

Эти задачи такого типа: «Даны два угла с общей верши­ной. Один из них равен 100°, другой - 80°. Будут ли эти углы смежными?»

Или: «Даны два угла с общей вершиной, равные друг дру­гу. Будут ли они вертикальными?»

В первой задаче ничего не сказано об общей стороне: есть она у данных углов или ее нет. В силу этого однозначный ответ дать нельзя: если углы имеют общую сторону, то они будут смежными, а если не имеют - то не будут.

Во второй задаче нет данных о сторонах углов: продол­жают они друг друга или нет. Если стороны одного продол­жают стороны другого, то углы будут вертикальными, а если не продолжают - будут два равных прилежащих угла.

В исследовании М.Б. Воловича, проведенном в ряде мос­ковских школ, в том числе в одной школе с математической специализацией, такие задачи были даны 232 хорошо и от­лично успевающим ученикам восьмого-девятого классов, обучающихся у восьми разных преподавателей. Около 90% учащихся дали неверные ответы. Они считали, что данные углы подходят под указанные в задачах понятия. На вопрос, почему они считают, что данные углы смежные, учащиеся отвечали: «Потому, что они в сумме составляют 180°». На вопрос, почему они считают, что во второй задаче даны вер­тикальные углы, отвечали: «Потому что они равные».

Как видим, школьники опираются не на систему призна­ков, указанную в определении, а лишь на отдельные призна­ки. В то же время определение этих понятий они знают. Сле­довательно, учащиеся определение запомнили, но работать с ним не научились.

Аналогичные ошибки ученики делают и на материале рус­ского языка. Например, на вопрос: «Слово изменяется по падежам, числам. Будет ли оно существительным?» - многие учащиеся отвечают утвердительно, что неверно, так как этими признаками обладает не только существительное, но и прила­гательное.

Причина всех этих ошибок - неумение применить логиче­ский прием подведения под понятие. Этот прием широко ис­пользуется в жизненной практике людей, причем человек не­редко встречается и с неопределенными ситуациями, когда главный вопрос состоит именно в том, может ли быть решена задача при данных условиях. Примером может служить диаг­ноз врача: чаще всего ошибки объясняются тем, что в ситуа­ции неопределенности, т.е. когда возможны несколько болез­ней, врач без получения сведений о недостающих признаках ставит диагноз.

Учащиеся допускают еще больше ошибок при выполнении классификаций, при выведении следствий из данных посылок. В то же время, как показывают исследования, многие из этих приемов учащиеся могут успешно усвоить уже в начальной школе, если работу вести планомерно и целенаправленно. Но с чего начать? В каком порядке формировать?

Естественно, что с любого логического приема работу на­чинать нельзя, так как внутри системы логических приемов мышления существует строго определенная последователь­ность, один прием строится на другом.

Вернемся к приему подведения под понятие и посмотрим, можно ли начинать формирование логических приемов мыш­ления с него. Для того чтобы решать вопрос о принадлежно­сти предмета к данному понятию, надо установить наличие у этого предмета системы необходимых и достаточных призна­ков. А это означает, что ученики к этому времени уже должны быть знакомы с понятиями необходимый признак и признак достаточный. Но эти понятия, в свою очередь, опираются на понятие существенный признак. Следовательно, учащиеся должны уметь дифференцировать признаки на существенные и несущественные. Последние, наконец, предполагают владе­ние понятием признак, свойство и умением выделять в предме­тах различные свойства. Как видим, усвоение приема подведения под понятие предполагает усвоение целой системы дру­гих логических знаний и операций: необходимых и достаточ­ных свойств, понимание того, чем отличается необходимое свойство от достаточного, что такое вообще свойства, как их выделять в предмете, чем отличается свойство существенное от свойства несущественного и др.

Значит, нельзя начинать формирование логического мыш­ления с приема подведения под понятие.

С чего же начинать?

Первое, чему необходимо научить учащегося, - это уме­нию выделять в предметах свойства. Дети первого класса обычно выделяют в предмете всего два-три свойства, в то время как в каждом предмете бесконечное множество различ­ных свойств. Так, если покажете детям карандаш и спросите: «Что о нем можно сказать, какой он?», - ученики ответят, что он красный (или назовут какой-то другой цвет), круглый (если он имеет цилиндрическую форму), - и все. Больше, чем два-три свойства, они не могут выделить. Поэтому необхо­димо специально обучать детей умению видеть в предмете множество свойств. Для этого полезно показать им прием по выделению свойств в предметах - прием сопоставления дан­ного предмета с другими предметами, обладающими другими свойствами. Заранее подбирая для сравнения различные пред­меты и последовательно сопоставляя с ними исходный, можно постепенно научить детей видеть в предметах множество та­ких свойств, которые ранее были от них скрыты.

Как только дети научатся выделять в предметах множество различных свойств, можно переходить к следующему компо­ненту логического мышления - формированию понятия об общих и отличительных признаках предметов¢.

' Методику формирования логических знаний и действии см. в главах 9 и 10 данной книги.

После того как учащиеся научатся выделять в предметах общие и отличительные свойства, можно сделать следующий шаг - научить детей отличать в предметах существенные (важные) свойства, с точки зрения определенного понятия, от свойств несущественных (неважных), второстепенных. Так, если вы знакомите детей с понятием «цветок», то покажите им, что цветы могут отличаться друг от друга очень многими свойствами: цветом, формой, величиной, количеством лепест­ков и т.д. Но у всех у них остается неизменным одно свойство: давать плод, что и позволяет называть их цветами. Если мы изменим это свойство - возьмем другую часть растения, - то ее мы уже не сможем назвать цветком. Это будут листья, ветки и т.д. Таким образом, если изменить несущественные свойст­ва, предмет будет относиться по-прежнему к тому же поня­тию, а если изменить существенное свойство, предмет стано­вится другим.

Показав это на нескольких примерах, важно указать, что таким путем можно отличить в предметах свойства сущест­венные (важные) от свойств несущественных (неважных). По­сле этого учащимся обязательно надо дать упражнения на практическое использование этого приема. Разумеется, при этом надо выбирать такие понятия, которые доступны пони­манию детей. Особенно важно при этом показать, что не все общие свойства в предметах являются свойствами существен­ными. Так, при работе с цветами легко видеть, что они, как правило, характеризуются яркостью, их цвет резко отличается от цвета других частей растения. Вместе с тем это общее для большинства цветов свойство не является существенным. На этом моменте следует особенно сосредоточить внимание де­тей, так как они легко принимают любое общее свойство предметов за свойство существенное. Причем эту ошибку допускают даже старшеклассники. Следовательно, надо пока­зать, что любое существенное свойство является общим для данного класса предметов, но далеко не всякое общее их свой­ство является существенным.

Мы рассмотрели два логических приема:прием сравненияпредметов, который дает возможность выделять множество свойств в предметах, иприем изменения свойств, который позволяет отличать свойства существенные от свойств несу­щественных. Как мы видели, эти приемы используются для ознакомления учащихся с рядом логических понятий (знаний): свойства, свойства отличительные и общие, свойства сущест­венные и несущественные. Другими словами, логические зна­ния - продукт выполнения определенных действий. И, наобо­рот, усвоение логических приемов мышления предполагает опору на определенные логические знания.

Так, понятия об общих и существенных признаках предме­тов оказываются необходимыми для усвоения целого ряда более сложных логических приемов. Некоторые из них будут рассмотрены ниже.

Прежде всего вернемся к приему сравнения. Когда мы предлагали использовать этот прием для выделения учащими­ся различных свойств в предметах, то указывали, что предме­ты для сравнения должны подбираться учителем, никаких специальных требований к сравнению не предъявляли. После знакомства учеников с различными видами свойств предме­тов прием сравнения можно формировать уже на более высоком уровне. Если этого не сделать, то у многих школьников он останется на житейском уровне: без осознания содержания этого приема и без умения произвольно и обоснованно ис­пользовать его как полноценное познавательное средство.

Анализ учебников и программ показывает, что действие сравнения необходимо учащимся уже в первом классе. Вместе с тем если его не сделать предметом специального усвоения, то оно оказывается не усвоенным большинством школьников до конца учебного года. Оказалось, что многие дети не пони­мают, что значит сравнить. Одни просто отказываются от ответа, а другие говорят, что сравнить - это «сказать, что больше, а что меньше». Только небольшой процент учащихся понимают смысл этого действия правильно. Наибольшие трудности дети испытывают при выделенииоснования для сравнения предметов. Они часто ориентируются не на общий для сравниваемых объектов признак (цвет, форма, длина и т.д.), а на конкретные количественные и качественные показатели этого признака. В силу этого одни ученики считают, что сравнивать, например, по цвету можно только предметы, имеющие один и тот же цвет, но с разной мерой его выраженности («более красный», «менее красный»). Другие, наоборот, считают, что сравнивать предметы по цвету можно только тогда, когда цвет у них разный. Это означает, что учащиеся еще не осознают цвет как общую характеристику предметов, а мыслят лишь на уровне конкретных разновидностей цвета. С этим надо считаться и постепенно учить детей видеть у разноокрашенных предметов, имеющих разную форму и т.д., общее свойство - наличие цвета, формы и т.д.

Начинать работу по формированию приема сравнения надо с выделения содержания этого приема, т.е. с выделения сла­гающих его действий. Сравнение будет корректным только тогда, когда оно используется, во-первых, при сравнении одно­родных предметов и явлений действительности (растений, зда­ний, животных и т.д.); во-вторых, когда сравнение производит­ся по существенным признакам. Сравнение предполагает уме­ние выполнять следующие действия: 1) выделение признаков у объектов; 2) установление общих признаков; 3) выделение ос­нования для сравнения (одного из существенных признаков); 4) сопоставление объектов по данному основанию.

Если учитель уже научил детей выделять в предметах об­щие и существенные свойства, то новыми будут лишь два последних компонента: выбор признака, по которому предполагается сравнение, и проведение сравнения именно по этому признаку. Учитывая вышесказанное, особое внимание необходимо обратить на выбор основания для сравнения.

Следует также подчеркнуть, что сравнение может идти как по качественным характеристикам того или иного свойства (например, цвету, форме), так и по количественным характе­ристикам: больше - меньше, длиннее - короче, выше - ниже и т.д.

При количественном сравнении необходимо наличие еди­ного образца (меры), с помощью которой и производится сравнение. Это очень важно подчеркнуть, так как учащиеся нередко в средних и даже старших классах это требование не учитывают: сравнивают, например, дроби без приведения к общему знаменателю; аналогичную ошибку школьники до­пускают и при работе с метрической системой мер.

Вначале в качестве меры может выступать один из сравни­ваемых предметов, в котором предварительно выделяется то свойство, по которому эти предметы будут сравниваться. Например, учитель может вызвать двух учеников и предло­жить классу сравнить их по росту. На вопрос учителя: «Как это сделать?» - ученики обычно отвечают: «Пусть померяют­ся». В этом случае один из сравниваемых учеников выступает в качестве меры. Такое сравнение называется непосредствен­ным. На его основе формируется сравнение опосредованное. Особенность этого вида сравнения состоит именно в том, что сравнение предметов происходит не непосредственно, а с по­мощью меры - опосредованно. При обучении детей умению работать с мерой очень важно, чтобы они осознали адекват­ность (соответствие) меры тем свойствам, по которым проис­ходит сравнение: предметы по длине сравниваются с помо­щью меры длины, по весу - с помощью меры веса и т.д.

Следующий шаг в формировании логического мышления учащихся - знакомство их с признаками необходимыми и достаточными. Научить детей различать эти признаки не так просто, так как объективно их отношения весьма сложны. Нередко даже взрослые думают, что всякий достаточный при­знак является одновременно признаком необходимым. Фак­тически же это не так. Вот один пример. Если у человека вы­сокая температура, то все понимают, что человек болен. Это означает, что признак «высокая температура» является доста­точным для признания человека больным. Однако этот при­знак вовсе не является необходимым, так как немало болез­ней, протекающих без температуры. Следовательно, отсутст­вие температуры не означает отсутствие болезни: человек может быть болен, а высокой температуры у него нет.

Даже в старших классах учащиеся допускают множество ошибок, связанных с неумением дифференцировать эти два вида признаков. В исследовании Г.И. Харичевой учащимся седьмых классов были предложены специальные задания, выполнение которых предполагает понимание характера при­знаков - необходимые, достаточные, необходимые и одно­временно достаточные. Вот одно из этих заданий:

«Известна теорема: «Диагонали ромба взаимно перпендикулярны». Объ­ясните, какая из двух формулировок этой теоремы справедлива: 1. Если четырехугольник ромб, то его диагонали взаимно перпендикулярны. 2. Если диагонали четырехугольника взаимно перпендикулярны, то данный четы­рехугольник есть ромб».

Результаты выполнения заданий показали, что только 24% учащихся справились с ними. Что касается указанного зада­ния, то его правильно выполнили 50% школьников (выбрали в качестве правильного первое определение). 26% учащихся ответили, что оба предложенных определения являются пра­вильными. Характерно, что эти ученики вообще не видели разницы в предложенных определениях. Они считали, что в обеих формулировках говорится об одном и том же, «только слова переставлены местами». Это означает, что они не пони­мают разницы между признаками необходимыми и признака­ми достаточными. Во втором определении указанные призна­ки являются необходимыми для ромба, но они не достаточны для его определения, так как этим требованиям удовлетворяет не только ромб, но и делтоид.

Ошибки допускаются при работе не только с математиче­ским, но и любым другим материалом. Так, например, уча­щимся восьмых-девятых классов было предложено следую­щее задание:

«Докажите, какие из данных слов - «краснота», «камни», «большой», «гвоздь» - являются прилагательными, а какие не являются».

Один из учеников совершенно правильно воспроизвел определение при­лагательного, но применить его корректно не смог. Вот его ответ: «Надо проверить по вопросу «какой». Если слово отвечает на вопрос «какой?», тогда оно прилагательное». Экспериментатор обратил внимание ученика на то, что в определении указано еще одно требование: прилагательные обозна­чают признаки предметов. «Как быть с этим требованием? Может быть, это лишнее требование и его можно исключить из определения», - продолжает экспериментатор. Ученик растерялся и выполнять задание отказался: «Ну, тогда я не знаю».

В данном случае ситуация аналогична предыдущей: ученик путает необходимые и достаточные признаки. То, что прила­гательное отвечает на вопрос «Какой?» - это признак необхо­димый: все прилагательные отвечают на этот вопрос. Любое слово, которое не отвечает на этот вопрос (не имеет этого признака), прилагательным не является. Однако одного этого признака недостаточно, чтобы выделить слова, являющиеся прилагательными. В самом деле, на вопрос «какой?» отвечают и слова, являющиеся причастиями: краснеющий, выходящий, бегущий и т.д. Вот почему для выделения прилагательных необходимо учитывать два необходимых свойства, которые в совокупности оказываются достаточными для выделения слов-прилагательных.

Непонимание разницы между необходимыми и достаточ­ными, необходимыми и одновременно достаточными призна­ками - широко распространенное явление среди учащихся старших классов, потому что эти важные логические знания не были предметом специального усвоения. Вместе с тем ука­занные виды признаков могут быть усвоены уже в начальной школе. Естественно, ученики при этом должны не просто за­учить определения этих признаков, а научиться работать с ними, т.е. выполнять определенные логические приемы мыш­ления. Прежде всего необходимо научить детей выводить следствия из факта принадлежности предмета к данному по­нятию. Это действие связано с понятием необходимых свойств предмета, поэтому его выполнение дает возможность овладеть этой категорией свойств.

Познакомить с этим действием можно с помощью хорошо известных учащимся предметов. Например, учительница, об­ращаясь к классу, говорит: «Ребята, я принесла карандаш. Он у меня в портфеле. Вы его никогда не видели. Можете ли вы что-нибудь сказать о нем?» Дети дают разные ответы: одни называют грифель, другие форму, третьи - корпус, который держит грифель, четвертые - цвет и т.д. Ответы детей анали­зируются с точки зрения обязательности у карандашей на­званного детьми признака. В результате проведенной работы выделяются два признака, без которых не может быть ни од­ного карандаша: наличие грифеля и какого-то корпуса, в ко­тором грифель закреплен.

Затем учительница говорит, что признаки, которые в обяза­тельном порядке есть у всех предметов данного класса, назы­ваются необходимыми. Отсутствие этих признаков приводит к тому, что предмет оказывается не относящимся к данному клас­су предметов. Так, если карандаш не будет обладать призна­ком - иметь корпус, то он из карандаша превратится в грифель.

После этого учащиеся выполняют еще ряд заданий на вы­ведение необходимых свойств. При этом, естественно, исполь­зуется и учебный материал. Так, в начальной школе ученики знакомятся с понятием отрезок. Учитель может предложить детям задание: «Известно, что линия является отрезком. Ска­жите, какими свойствами обладает эта линия в обязательном порядке?» Учащиеся должны указать следующие свойства: а) это часть прямой; б) она ограничена с двух сторон. Наличие этих свойств вытекает из факта принадлежности линии к по­нятию отрезок прямой.

Графически действие выведения следствий может быть изо­бражено так:

1-е свойство

2-е свойство

3-е свойство

Количество свойств, которые могут быть при этом указа­ны у предмета, зависит от содержания самого понятия и от того, насколько продвинулись учащиеся в изучении его. Так, например, если школьники только приступили к изучению понятия треугольник, то они смогут указать лишь на те его свойства, которые содержатся в определении: а) замкнутая фигура; б) состоит из трех отрезков прямой. После изучения всех теорем, относящихся к треугольнику (в более старших классах), учащиеся смогут назвать дополнительные свойства: сумма внутренних углов равна 180°; сумма двух сторон боль­ше третьей и т.д.

Таким образом, прием выведения следствий должен быть введен в начальной школе, а формирование его должно про­должаться во всех последующих классах.

После знакомства с необходимыми признаками вводится понятие признаков достаточных и признаков необходимых и одновременно достаточных. Здесь важно показать, что не всякий необходимый признак является достаточным. Нередко учащиеся допускают подобные ошибки. Например, четырех­угольник, имеющий хотя бы два прямых угла, они считают прямоугольником. Это неверно, так как этими свойствами обладает и прямоугольная трапеция. И для нее, и для прямо­угольника - это свойства необходимые, но не достаточные. И наоборот, не всякое достаточное свойство является необходи­мым, на что уже было указано раньше.

Вот теперь мы подошли к действию подведения под поня­тие. Отнесение любого объекта к тому или иному понятию предполагает установление наличия у этого объекта призна­ков данного понятия, достаточных или необходимых и одно­временно достаточных.

Как видим, формированию этого приема предшествует ус­воение целого ряда логических знаний и требующих их исполь­зования действий. Если же этого не сделать, то полноценного усвоения приема подведения под понятие не произойдет.

Что же представляет собой этот прием, какую конкретную деятельность должен выполнить ученик, чтобы безошибочно подводить предметы под то или иное понятие? Во-первых, учащиеся должны научиться выделять понятие, под которое требуется подвести данный объект. Рассмотрим случай подве­дения равностороннего треугольника под понятие равнобед­ренный треугольник. Последнее и будет таким понятием. Во-вторых, надо установить, при каких условиях данный объект может относиться к данному понятию. В нашем случае: при каких условиях треугольник может быть равнобедренным. Известно, что для этого он должен иметь две равные стороны. От учащихся потребуются знание определения равнобедрен­ного треугольника и умение вывести из него систему необхо­димых и достаточных признаков. Как показывает опыт, уче­ники, зная определение, не умеют анализировать его.

После этого ученику надо установить, обладает ли данный объект этими признаками. В нашем случае: обладает ли рав­носторонний треугольник признаками равнобедренного. Для этого необходимо воспроизвести определение равносторонне­го треугольника, сопоставить данные в нем признаки с требуемыми, для чего также необходимо специальное обучение.

Важно показать учащимся необходимость учета именно всей системы необходимых и достаточных признаков. Из школьной практики известно, что одна из типичных ошибок учащихся состоит в том, что они при подведении заданных объектов под соответствующие понятия учитывают лишь некоторые признаки из числа необходимых и достаточных и поэтому относят к понятию и такие предметы, которые имеют с объектами данного класса лишь некоторые общие признаки.

Так, в одном из опытов, проведенном в московской школе, учащиеся седьмого класса безошибочно воспроизводили определение окружности, но когда им предъявили эллипс, замкнутую кривую произвольной формы и спросили, можно ли эти фигуры назвать окружностью, - они ответили ут­вердительно. Беседа с учениками показала, что при распознавании окружно­стей они опираются не на всю совокупность признаков, которые указаны в определении окружности и которые они заучили, а только на замкнутость кривой и наличие во внутренней области точки, которую они называют центром. Аналогично учащиеся шестых-седьмых классов нередко смежными углами соглашаются назвать любые два угла, составляющие в сумме 180°. Они хорошо знают, что любые смежные углы обладают этим свойством, т. е. они усвоили, что это свойство является необходимым для всех объектов, относящихся к данному классу предметов. Но школьники его используют и как достаточное: считают, что все объекты, обладающие этим свойством, относятся к данному классу предметов, что уже неверно, так как этим свой­ством обладают и объекты, не относящиеся к данному классу. Так, прямые вертикальные углы также в сумме составляют 180°, а смежными не являются.

В связи с этим особенно важно специально поработать над системой свойств, в совокупности являющихся достаточными для определения объектов данного класса. При этом обязатель­но надо показать, что учет лишь одного из свойств данной сис­темы не позволяет определить объекты однозначно, так как это свойство может быть общим для предметов разных классов.

Все указанные компоненты приема подведения под поня­тие связаны с определенными предметными знаниями и спе­цифическими действиями, характерными для данного предме­та; в нашем случае - геометрии. В самом деле, учащиеся, про­веряя наличие искомых признаков у данного объекта, могут использовать различные методы, характерные для математи­ки, химии, русского языка и т.д. Но во всех случаях общие требования к подведению (проверка наличия определенной системы признаков) задает логика. Логика же задает требова­ния и к оценке полученных результатов. Их можно сформули­ровать следующим образом. Предмет относится к данному понятию в том и только в том случае, когда он обладает всей системой необходимых и достаточных признаков, что можно изобразить так:

признак 1 «+»

признак 2 «+»

……… +

……..

признак n «+»

Если предмет не обладает хоть одним из них, то он не от­носится к данному понятию, что можно изобразить так:

признак 1 «+» (?)

признак 2 «+» (?)

………… _

признак m «-»

признак n «+»

При этом следует отметить, что отрицательный ответ бу­дет при отсутствии любого признака.

Если же нет положительной информации хотя бы про один признак, то при наличии всех остальных признаков ответ оста­ется неопределенным: неизвестно, принадлежит или не принад­лежит предмет к данному понятию. Это можно изобразить так:

признак 1 «+»

признак 2 «+»

………… ?

признак m «?»

признак n «+»

Правило подведения под понятие и умение корректно пользоваться им при работе с любыми понятиями относится к логическому компоненту данного приема.

Учащиеся, получая задания на подведение объектов под различные понятия, постепенно усваивают этот важный при­ем. При работе с ним особое внимание надо уделить третьему случаю: ответ неопределенный. Задания с неопределенными условиями неизменно дают большой процент ошибок. Этот случай трудней усваивается, чем другие, даже при целена­правленной работе. Отсутствие указаний о том или ином при­знаке учащиеся обычно расценивают как отсутствие самого признака. Например, в задаче: «Даны две пересекающиеся прямые. Будут ли они перпендикулярными?» - учащиеся дают отрицательный ответ. Они мотивируют это тем, что в условии не сказано, что прямые пересекаются под прямым углом. От­вет неверный, так как в условии в равной мере не сказано, что прямые пересекаются не под прямым углом. Следовательно, об этом признаке мы не получаем никакой информации, что и создает ситуацию неопределенности: может быть, угол пря­мой, а может быть, не прямой. В силу этого правильный ответ в таких задачах: «Неизвестно».

Говоря о действии подведения под понятие, мы подчерки­вали, что объект относится к тому или иному понятию тогда и только тогда, когда обладает всей системой необходимых и одновременно достаточных признаков. Но так бывает только при подведении под понятия, где признаки связаны союзом «и - и» (конъюнктивная структура понятия). Кроме них, есть понятия с другой структурой признаков: связанных союзом «или - или» (дизъюнктивная структура признаков). В этом случае правило подведения под понятие другое: для отнесения предмета к данному классу предметов достаточно наличия лишь одного из указанных признаков. При работе с учащи­мися эти два случая подведения под понятие необходимо различать. Если же этого не делать, то у учащихся может не сформироваться правильных приемов подведения, и они бу­дут ошибаться.

Как мы видели, задачи на подведение под понятие с дизъюнктивной структурой признаков вызывают у учащихся серьезные трудности. Они доставляют немало хлопот и взрослым, если они не владеют этим приемом. Характерно, что задачи: «Я тебе мать, а ты мне не дочь», «У двух зрячих есть слепой брат, но у него нет братьев» и т.п. - нередко относят к головоломкам.

Какой же логический прием подведения под понятие тре­буется в подобных случаях? Схематически характер связей в данном случае следующий:

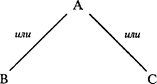
Если в ранее показанном случае отсутствие хоть одного признака означало непринадлежность предмета к данному понятию, то в данном случае это не так: если нет признака В, то мы не имеем права делать отрицательный вывод. Мы должны обратиться к признаку С. Так, в случае понятия «мать» отсутствие дочери не мешает быть матерью, для этого достаточно иметь сына.

Правило подведения под понятие с дизъюнктивной структурой признаков уже другое: «Предмет относится к данному |понятию, если он обладает хотя бы одним признаком из числа оказанных. Если же предмет не обладает ни одним из этих признаков, то он не относится к данному понятию. Если ни про один из признаков нет точных сведений (неизвестно, есть он или его нет), то мы не может сказать, относится или не относится этот предмет к данному понятию».

Схематически это правило можно изобразить так:

1. признак 1 «-»

признак 2 «-»

………….«-» +

………….«-»

признак n «+»

2. признак 1 «-»

признак 2 «-»

………….«-» -

…………. «-»

признак n «-»

3. признак 1 «?»

признак 2 «?»

………. «?» ?

………. «?»

признак n «?»

4. признак 1 «?»

признак 2 «-»

……… «?» ?

……… «-»

признак n «?»

Знакомство с этим приемом можно начать с указанных про­стых житейских примеров, а потом уже перейти и к учебному материалу. Так, когда учащиеся изучают виды предложений, то ряд понятий имеет дизъюнктивную структуру признаков. При­мером могут служить неполные предложения. Для отнесения предложения к этому понятию достаточно одного из двух при­знаков, соединенных союзом «или - или»: или нет подлежаще­го, или нет сказуемого. Таким образом, этот прием мышления необходим для успешного усвоения учебного материала и его формирование следует начинать уже в начальной школе.

Если при усвоении нескольких понятий (одни из которых имеют конъюнктивную структуру признаков, а другие - дизъюнктивную) учитель научит учеников логически строго выполнять действие подведения под понятие, то в дальнейшем это действие они будут успешно использовать при работе с любыми понятиями.

Уже в начальной школе можно приступить к работе над определениями. Но до этого дети должны усвоить отношения между родовыми и видовыми понятиями. При этом особое внимание следует обратить на то, что видовое понятие обяза­тельно обладает всеми свойствами родового, а родовое явля­ется следующей ступенью обобщения. При этом следует отме­тить, что в определение входят только необходимые и одно­временно достаточные признаки.

Без понимания видо-родовых отношений учащиеся не смогут полноценно усвоить программный материал. Так, уже при обучении детей звуковому анализу учитель вводит целую систему видо-родовых отношений: вначале вводится понятие о звуке, затем - о гласных и согласных звуках, а согласные, в свою очередь, делятся на мягкие и твердые. Как показал наш опыт работы в одном из детских садов г. Москвы (детсад № 936), дети шести лет способны понять видо-родовые отношения. Характер этих отношений можно за­фиксировать в виде трех цветных кружков, вписанных один в другой. Например, желтый круг означает все множество звуков, а красный круг внутри желтого - означает гласные звуки, зеленый круг на фоне желтого - согласные звуки, а мягкие и твердые согласные можно обозначить кругами разного цвета на фоне кругов, обозначающих согласные. В этом случае дети наглядно будут видеть, что мягкие (твердые) согласные - это звуки, являющиеся и согласными, и звуками.

Желательно познакомить учащихся и с отношениями со­подчинения. Так, в курсе природоведения можно показать, что к понятию лиственных деревьев относятся самые разные виды, а лиственные, в свою очередь, соподчинены с хвойны­ми: их вместе объединяет понятие «дерево». Все это заложит основу для формирования более сложных приемов логическо­го мышления, в том числе - для понимания структуры опреде­лений, с которыми ученики работают на протяжении всего школьного обучения.

В школе учащийся не знакомится с логической структурой определений: он просто заучивает огромное число различных конкретных определений. И если ученик что-то забывает в определении, то не может путем логического рассуждения восстановить забытое, так как не знает структуры определе­ний, не владеет правилами их построения.

Даже в старших классах учащиеся теряются, когда перед ними встает задача по оценке предложенных определений. Так, в исследовании Н.А. Подгорецкой ученикам десятых клас­сов было предложено 20 определений простейших геометри­ческих понятий: ромб, квадрат, прямоугольник, параллело­грамм, четырехугольник. Среди предложенных определений были как правильные, так и ложные. Школьники должны были указать как те, так и другие. Ошибочные определения содержали такие дефекты, как пропуск ближайшего родового понятия (определение квадрата, например, как геометриче­ской фигуры), наличие только лишь необходимых признаков, неточное указание видовых признаков и др.

Оказалось, что даже хорошо и отлично успевающие уча­щиеся в среднем дали 65% правильных ответов, остальные их ответы были ошибочными. Например, многие учащиеся ука­зали как верное такое определение параллелограмма: «Парал­лелограммом называется четырехугольник, две противопо­ложные стороны которого параллельны». Это определение ошибочное, так как указанные в нем признаки не позволяют . отличить параллелограмм от трапеции. Аналогично опреде­ление квадрата как геометрической фигуры, все стороны и все углы которой равны между собой, многие учащиеся признали правильным, что неверно. Их не смутило то, что квадрат оп­ределяется не через ближайший род (прямоугольник), а через весьма отдаленное понятие - геометрическая фигура. Учащиеся делали ошибки как на расширение, так и на сужение объе­ма определяемых понятий.

Таким образом, видо-родовые отношения понятий, логи­ческие правила определений должны войти в программу фор­мирования логического мышления учащихся.

Следующий логический прием, который широко использу­ется в процессе обучения и без которого невозможно полноцен­ное мышление человека, - прием выведения следствий с соблюде­нием требований закона контрапозиции. Этот прием, как и пре­дыдущие, также обычно не выступает в школе в качестве пред­мета специального усвоения. В силу этого далеко не все уча­щиеся даже старших классов понимают, что одно и то же след­ствие может быть связано с разными основаниями, и поэтому от наличия следствия нельзя переходить к утверждению нали­чия основания. Так, учащиеся правильно указывают, что если углы смежные, то их сумма равна 180°. Но нельзя утверждать, как это делают некоторые ученики, обратное: если сумма углов равна 180°, то они являются смежными (прямые вертикальные углы равны в сумме 180°, но они не являются смежными). Одно и то же следствие (сумма углов 180°) имеет разные основания.

Учащимся восьмого класса были предложены пары посы­лок, из которых требовалось сделать выводы. Вот некоторые из них: «Если у человека повышена температура, то он болен. У человека не повышена температура». «Если данный четырех­угольник является ромбом, то его диагонали взаимно перпен­дикулярны. Данный четырехугольник не является ромбом».

Подавляющее большинство учащихся и в первом, и во втором случае дали неверные ответы: они сделали вывод, что человек, не имеющий повышенной температуры, не болен, и что у данного четырехугольника диагонали не взаимно пер­пендикулярны.

Суть их ошибки состоит в том, что они сделали вывод с нарушением закона контрапозиции. В чем состоит этот закон? Этот закон нам указывает, когда мы имеем право делать вы­вод, а когда не имеем.

Для удобства работы изобразим сущность закона контрапозиции схематически.

1. Если А, то В 2. Если А, то В

Дано А Дано не В

Вывод: В Вывод: не А

3. Если А, то В 4. Если А, то В

Дано не А Дано В

Вывод сделать нельзя Вывод сделать нельзя

Первый случай простой: если имеет место А, то из этого следует В. Нам известно, что А налицо. Следовательно, В будет иметь место в обязательном порядке (необходимо следует). Во втором случае известно, что В отсутствует. Но если отсутствует В, которое есть необходимый признак А, то, есте­ственно, мы имеем право сделать вывод о том, что нет и А.

В двух последних случаях вывода сделать нельзя по ука­занным данным. В самом деле, известно, что есть В. Это след­ствие. Известно, что А имеет обязательно следствие В, но это вовсе не означает, что только А имеет такое следствие. По­этому мы не можем сделать вывод, что в этом случае есть А. Аналогично в последнем случае известно, что нет А, но в силу только что сказанного нельзя утверждать, что нет и В, так как оно может быть следствием другого основания. Но именно эту ошибку и допустили ученики. В самом деле, если у челове­ка высокая температура, то можно сделать вывод, что он бо­лен. Но вывод о заболевании можно сделать и на другом ос­новании. Отсутствие высокой температуры вовсе не доста­точно для заключения об отсутствии болезни: очень часто болезнь протекает без температуры. Аналогично положение и во втором случае.

Умение правильно делать выводы надо формировать с первого класса. Для этого учитель может использовать такие, например, задания: «Ребята, вы хорошо знаете, что зимой березки стоят без листьев. Если вы увидели березку без листь­ев, можете вы сказать, что на улице зима?» Или: «Мы знаем, что если идет дождь, то тротуары сырые. Представьте себе, что вы утром вышли из дома и увидели на тротуаре лужицы. Можно ли утверждать, что был дождь?» Учащиеся обычно дают разные ответы. Их следует проанализировать и объяснить: почему они верные или неверные.

Необходимо постепенно подвести школьников к обобщен­ному выражению закона контрапозиции и дать его схематическую запись. При этом важно показать ученикам, что форма «если, то» не всегда есть связь основание-следствие, она может быть условной связью: например, «Если я закончу работу пораньше, то прочитаю эту книгу». Наличие времени не есть причина, по которой человек читает книгу: это лишь условие, при котором он совершит это действие, имеющее свою причину. В тех случаях, когда «если, то» отражает объективную, закономерную связь явлений, следствие обязательно будет иметь место. В самом деле, если четырехугольник является ромбом, то его диагонали всегда перпендикулярны. В случае условной связи такого обязательного следования нет. В приведенном примере человек может закончить работу тогда, когда намечал, и все-таки книгу не прочитать. Может случиться что-то непредвиденное (плохо себя почувствовал, возникла необходимость выполнить какую-то работу и т.д.).

Очень важным приемом логического мышления, исполь­зуемым в процессе всего школьного обучения, является также прием классификации. Часто этот логический прием оказыва­ется не сформирован даже у людей с высшим образованием.

Специальное исследование Н.А. Подгорецкой умения про­водить классификацию старшеклассниками, а также людьми, уже окончившими среднюю школу, показало, что этот прием усвоен ими плохо. Так, только 20% старшеклассников смогли правильно выбрать критерий для классификации, ни один учащийся не сумел соблюсти координацию объема и содержа­ния классифицируемых классов объектов.

В задании на классификацию видов треугольников были допущены следующие типичные ошибки: 1) смешение критери­ев классификации на одном уровне (делили треугольники, на­пример, на прямоугольные, равнобедренные и равносторон­ние); 2) сужение объема понятий классификации (многие учени­ки не указали вида разносторонних треугольников); 3) наруше­ние иерархии: большая часть старшеклассников не понимает, что равносторонний треугольник является частным случаем равнобедренного. Аналогичные ошибки были допущены при классификации видов предложений, видов поверхности суши.

Все это говорит о том, что без специальной работы прием классификации усваивается неудовлетворительно. В состав этого приема входят такие действия, как выбор критерия для классификации; деление по этому критерию всего множества объектов, входящих в объем данного понятия; построение ие­рархической классификационной системы.

Естественно, что формирование этого приема должно про­исходить постепенно, на материале разных учебных предметов.

Не останавливаясь на других приемах логического мыш­ления, укажем, что все рассмотренные нами необходимы для полноценного усвоения изучаемых в школе предметов: дейст­вия, стоящие за этими приемами, и будут служить средством усвоения различных предметных знаний. Важно отметить и то, что на основе этих приемов можно формировать и более сложные методы логического мышления.

Для того чтобы показать важность формирования рас­смотренных элементарных логических приемов, проанализи­руем один из труднейших методов доказательства, с которым ученики встречаются при изучении геометрии, - доказатель­ство методом от противного. Легко показать, что в его со­держание входят в основном рассмотренные нами простейшие логические операции. В самом деле, прежде всего при доказа­тельстве методом от противного строится предположение, что объект, данный в условии теоремы, не обладает теми свойст­вами, которые указаны в заключении теоремы.

Так, например, в одной из теорем о параллельных прямых говорится, что если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.

Мы допускаем, что прямые не параллельны. В основе этого лежит так называемая дихотомическая классификация: все прямые на плоскости мы можем поделить на два класса - пересекающиеся и не пересекающиеся, т.е. параллельные. Это значит, что данные нам в условии теоремы прямые обя­зательно должны относиться к одному из этих классов.

Если мы докажем, что прямые не относятся к одному, то они обязатель­но должны относиться ко второму классу.

Мы предполагаем, что они относятся к пересекающимся прямым. После этого мы пользуемся вторым известным уже нам действием - действием выве­дения следствий: мы начинаем получать последовательно все те свойства, которые необходимо следуют из факта принадлежности прямых к классу пере­секающихся. Постепенно мы доходим до такого свойства, которое противоре­чит данным условиям. Значит, с одной стороны, если прямые относятся к пере­секающимся, то они обязаны обладать выведенным свойством, но нам извест­но, что они этим свойством не обладают. Араз прямые не обладают хоть од­ним свойством из системы необходимых, то они не могут относиться к данному классу объектов. Но если они не относятся к пересекающимся, то они могут относиться к не пересекающимся, т. е. к параллельным.

Итак, этот прием, обычно плохо понимаемый учащимися даже старших классов, оказывается построен на нескольких простых действиях: дихотомической классификации, выве­дении следствий, на понятии необходимых свойств. Если все эти компоненты сформировать, то, как показали опыты, учащиеся успешно усваивают и доказательство методом от противного, и доказательства другими методами, что сейчас у большинства учеников вызывает затруднения даже в старших классах.

Мы рассмотрели первый компонент познавательной дея­тельности - логические приемы мышления. Важность их фор­мирования у учащихся не требует доказательств, это очевид­но. Именно поэтому задача формирования логического мыш­ления ставится перед всеми учителями, при изучении всех предметов. Однако такая общая постановка задачи явно не­достаточна. Как мы видели, логическое мышление нельзя фор­мировать с любого приема: они связаны между собой внутрен­ней логикой, поэтому могут быть сформированы только в оп­ределенной последовательности.

Второе важное положение состоит в том, что приемы ло­гического мышления оказываются не усвоенными значитель­ным числом школьников не только в начальных классах, но и в старших. Объясняется это тем, что в процессе обучения учи­теля не делают их предметом специального усвоения, не рас­крывают перед учащимися их структуру, не формируют тех логических понятий, которые необходимы для понимания и правильного выполнения логических приемов мышления.

Вывод, который вытекает из всего вышесказанного, за­ключается в том, что ужев начальной школе при построении содержания обучения необходимо предусмотреть всю систему логических приемов мышления, необходимых для работы с планируемыми предметными знаниями, для решения задач, предусмотренных целями обучения. При этом важно отметить, что хотя логические приемы формируются и используются на каком-то конкретном предметном материале, в то же время они не зависят от этого материала, носят общий, универсаль­ный характер. В силу этого логические приемы, будучи усвое­ны при изучении одного учебного материала, могут в даль­нейшем широко применяться при усвоении других учебных предметов как готовые познавательные средства.

Следовательно, при отборе логических приемов, которые должны быть усвоены при изучении какого-то предмета, сле­дует учитывать межпредметные связи. Если какие-то логиче­ские приемы мышления были сформированы ранее - при изу­чении предыдущих предметов, то при усвоении данного пред­мета нет необходимости формировать их заново. Эти приемы просто используются для усвоения данных знаний. Предме­том специального усвоения должны быть только такие логи­ческие приемы, с которыми учащиеся встречаются впервые.