Порядок и хаос в системе
Существуют два вида движения частиц (объектов) в сложных системах (16):
движение когерентное (упорядоченное), когда все объекты в системе движутся (реагируют на воздействие) согласованно;
движение неупорядоченное (неуправляемое), когда все объекты в системе движутся хаотически (реагируют на воздействие несогласованно).
Чтобы совершить движение (взаимодействие отдельных частиц) объектов внутри системы, нужно совершить какую-то работу (воздействовать на систему).
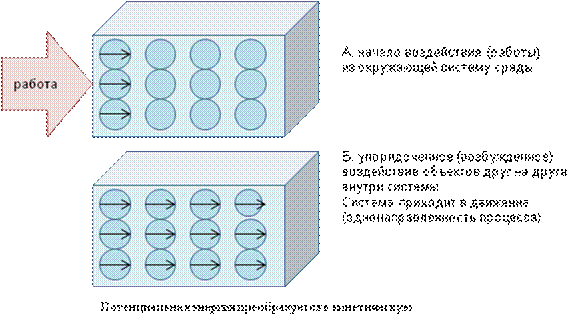
Рис. 8. Перенос энергии в системе при совершенной над ней работой
Совершая над системой работу, на нее оказывается воздействие извне, из окружающей среды, и это внешнее воздействие из окружающей систему среды вынуждает двигаться частицы (объекты) системы упорядоченно (рис. 8), а если система совершает работу над окружающей средой, она так же вызывает в ней упорядоченное движение.
При нагревании системы ее частицы (объекты системы) начинают двигаться неупорядоченно, а когда теплота переходит от объекта к системе, в ней возникает неупорядоченное движение (рис. 9).
Через какой-то отрезок времени неупорядоченность движения внутри системы приводит к тому, что внутри системы происходит равномерное распределение состояния возбуждения объектов (частиц), энергия (теплота), переданная системе, рассеивается равномерно внутри ее, и система стабилизируется, становится конечной (стационарной) (рис. 10).
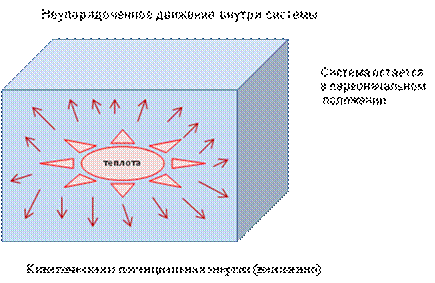
Рис. 9. Воздействие на систему теплотой
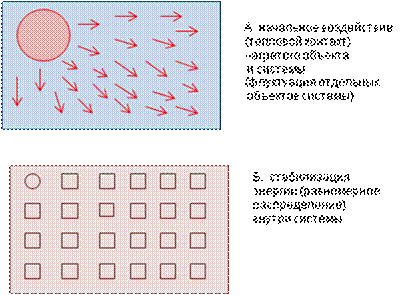
Рис. 10. Переход неупорядоченности внутри системы в стационарное (стабильное) состояние
Энергия, поступившая в систему, стремится рассеяться, распределяясь внутри системы, аналогично, поступившая из системы в окружающую среду, энергия рассеивается внутри среды. Данный процесс сопровождает любое естественное изменение. Рассеяние энергии следует понимать не только как ее пространственное рассеяние по объектам (частицам) системы, но и как разрушение упорядоченности объектов внутри системы. При этом энергия всегда стремиться к рассеянию, что соответствует второму началу термодинамики, а ее рассеяние всегда направленное.
Процесс взаимного перехода теплоты и работы естествен и в основе своей предполагает их различие свойств: работа предполагает упорядоченное движение, а теплота – неупорядоченное. В зависимости от того, как они взаимодействуют (порядок, последовательность и сила воздействия), зависит и взаимный переход из неупорядоченного движения в упорядоченное, и наоборот (14).
Рассеяние энергии (ее диссипация) сопровождается естественными процессами, и запасы энергии системы приводят к хаосу внутри ее. Естественный ход процессов в мире соответствует понижению качества энергии, а мерой беспорядка, хаоса является энтропия, потому что любые самопроизвольные изменения сопровождаются возрастанием энтропии. Отражением же отсутствия хаоса является высокое качество энергии.
Если определить энтропию системы как функцию S, характеризующую любые самопроизвольные изменения системы, а хаос охарактеризовать величиной W, как мерой рассеяния энергии в системе (Вселенной как высшей системе), то взаимосвязь энтропии и хаоса, как крайнего ее выражения, можно выразить формулой (соотношением Больцмана) (16):
S = k·logW, (1)
где:
k – фундаментальная мировая постоянная Больцмана.
Данное выражение отражает основу механизма изменения на микроскопическом уровне, связь макро- (S) и микромира (W), раскрывающего «скрытый» механизм происходящих изменений в системе.
В своей формуле Больцман опирался на теорию вероятностей, которая оперирует с количественной мерой случайных величин, применительно к тепловому движению.
В любом первоначальном состоянии системы (рис 11), до воздействия на нее, независимо от того, находится система во внутреннем возбуждении (система 1) или в спокойном состоянии (система 2), величина W = 1, а так как log W = lg 1 = 0, то и энтропия тоже нулевая, а энергия обладает идеальным качеством.
Но как только системы начинают взаимодействовать между собой (обмениваться энергией, теплотой), возбуждение системы 1 передается в систему 2, а невозбужденная система 2 в результате воздействия начинает «гасить» возбуждение частиц (объектов) системы 1. Величина W примет значение числа различных способов выбора одного невозбужденного объекта (частицы) системы 1 (16).
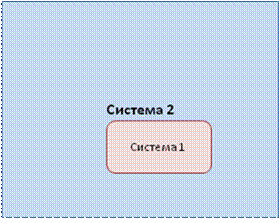
Рис. 11. Состояние систем 1 и 2, когда частицы (объекты) системы 1 находятся в возбужденном состоянии, а частицы системы 2 – в невозбужденном.
Если принять возбуждение частиц (объектов) системы 1 за 100% в абсолютных единицах (100), то невозбужденная частица х (рис. 12) лишится одного из 100 способов возбуждения, и тогда величина W = 100.
Так как неизвестно, какая частица системы 1 прекратит возбуждение, то log x примет значение ln x с основанием e (иррациональным числом, равным 2,78...), а ln 100 = 4,61.
При k=1 энтропия будет равна 4,61 (энтропия системы 1 возросла), появилась хаотичность с неопределенной частицей х, потерявшей возбуждение (рис. 12).
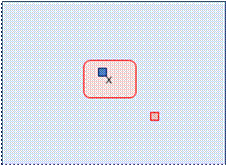
Рис. 12. Взаимодействие систем 1 и 2 с потерей возбуждения одного из объектов (частиц) системы 1 и получением возбуждения одной из частиц системы 2.
Адекватным образом возбуждение частицы х из системы 1 передастся неизвестной частице (объекту) в системе 2 (на рис. 12), и процесс, обладающий однонаправленностью, продолжится на другие частицы в системах 1 и 2.
Полное число перемещений возбуждения из системы 1 составит 100х99 = 9900, но данное число перемещений в силу случайности процесса в системе 1 составит 4950, отсюда: W = 4950.
В результате возбуждения объекта (частицы) энтропия S системы 1 возросла до величины ln 4950 = 8,51. В системе 2 количество возможностей выбора составит число j.
Примем значение j равным (Эткинс П., 1987) (16) 1500, тогда ln 1500 = 7.31, но так как одна из частиц у в системе 2 возбуждена, то полное число различных расположений частицы у будет равно половине значения 1500х1490, или 1 124 250, отсюда ln 1 124 250 = 13,93 (энтропия системы 2).
Так как условно принимаем размер системы 2 больше размеров системы 1 (как нагреватель – источник теплоты, система 1 расположена внутри системы 2), то энтропия системы 2 больше энтропии системы 1 в 2 раза, и одно возбужденное состояние в системе 2 может быть распределено по большему числу положений, чем в системе 1.
Число размещений может возрастать более и более, но, в соответствии с формулой Больцмана, рост энтропии растет в логарифмической последовательности, и даже при числе Авогардо, превышающем 1023, натуральный логарифм (энтропия) его составит 54,7 (рис. 13).
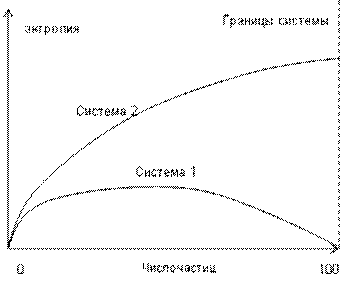
Рис. 13. Зависимость энтропии систем 1 и 2 от числа возбужденных состояний, перемещенных из системы 1 в систему 2 (при одинаковой температуре обеих систем)
Такой рост энтропии объясним не только математически. Энтропия систем 1 и 2 в начале их взаимодействия возрастает, но по мере роста перемещений возбуждение-невозбуждение всех частиц системы 1 достигает предела и доходит до 50%, ее энтропия начинает падать, и в системе 1 примет значение, равное 0, то есть система 1 ввиду ограниченности размера по сравнению с системой 2 придет в исходное состояние (см. график на рис. 13).
В системе 2 с получением энергии (тепла) от системы 1 энтропия системы 2 возрастает быстрее, но энергии (тепла) системы 1 недостаточно для того, чтобы привести 50% частиц системы 2 в возбужденное состояние (число возбуждений равняется числу возбуждений частиц системы 1), поэтому энтропия системы только повышается до определенного значения (приблизительно в 2 раза выше максимальной энтропии системы 1) (рис. 13).
Естественное направление потока энергии из системы 1 в систему 2 совпадает с направлением движения теплового потока (ингредиента температуры) (16):
температура = А / ln (число невозбужденных частиц /число возбужденных частиц)
Энтропия системы 2 при этом будет равной значению В на графике (рис. 14), но при установлении стабильного положения в обеих системах (равномерном распределении энергии по всем системам) энтропия системы 1 станет нулевой, а энтропия системы 2 при максимальном возрастании в ней температуры от нагревателя (системы 1) и выравнивании температуры с нагревателем снизится (точка А на графике рисунка) до определенного уровня, адекватного приложенной к ней теплоты.
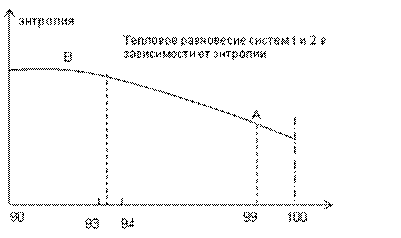
Рис. 14. График изменения величины энтропии в системе 2.
Аналогичным образом охлаждение системы 1 до теплового равновесия соответствует возрастанию ее энтропии от максимального значения до падения к нулю.
Наступает термическое равновесие двух систем, равное усредненному состоянию систем, при этом, чем больше способов достижения данного состояния, тем выше вероятность его достижения (10).
Отсюда следует, что тепловое равновесие соответствует наиболее вероятному состоянию систем, при этом, чем больше размеры системы, тем больший промежуток времени требуется для установления термического равновесия. Так, для нашей Вселенной этот временной промежуток с момента зарождения ее (первичного взрыва) составляет приблизительно три десятка миллиардов лет, после чего, вероятно, Вселенная перестанет сущесвовать.
Однонаправленность естественных процессов предопределяет все явления, происходящие в окружающем мире. Рассеяние (деградация) энергии происходит с начала зарождения Вселенной, носит случайный характер, как путем перемещения носителей энергии, так и путем ее перехода от одного носителя к другому.
Универсальное свойство этих явлений происходит неравномерно, то испытывая подъемы созидания, то разрушения, при этом после каждого периода созидания разрушительный этап обладает еще большей разрушительной силой.
Природа избрала сложный путь движения к хаосу за счет накопления энтропии и снижения качества энергии на каждом этапе однонаправленного движения, при этом сам хаос обладает созидательной способностью преобразования систем в новые структуры, с возрастанием степени хаоса в целом во Вселенной.
Дата добавления: 2016-09-20; просмотров: 1164;
