Приближенное интегрирование функций
9.1 Цель работы
Целью работы является закрепление знаний, полученных в лекционном курсе «Вычислительная математика» по разделу «Приближенное интегрирование», приобретение навыков использования соответствующих численных методов с применением программных средств автоматизации вычислений.
9.2 Задание
Для выполнения лабораторной работы рекомендуются следующие исходные данные в таблице 9.1
Диапазон изменения x для функции F(x) равен [0,1] , точность вычислений принять равной ±0.01.
Таблица 9.1
| xi | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 | Y8 | Y9 | Y10 |
| 0.25 | ||||||||||
| 0.5 | ||||||||||
| 0.75 | ||||||||||
| F(x) | ex | 2ex | 3ex | 4ex | 5ex | 6ex | 7ex | 8ex | 9ex | 10ex |
9.3 Теоретические сведения
Задача приближенного интегрирования возникает для сложных аналитических функций или функций, заданных дискретными данными.методы численного интегрирования основаны на аппроксимации определенного интеграла суммой составных площадей.
Численное интегрирование в отличие от численного дифференцирования является устойчивой процедурой и имеет тенденцию снижения влияния погрешности исходных данных на конечный результат.
В общем виде задача состоит в нахождении величины
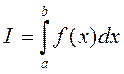 (9.1)
(9.1)

|
|



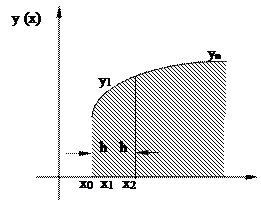
Рис.9.1 Приближенное вычисление определенного интеграла
Определенный интеграл (9.1) численно равен площади, заштрихованной на рис.9.1. Если промежуток [а,b] разделить на конечное число участков 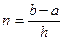 с шагом h , то задача (9.1) сводится к решению большого числа более простых задач.
с шагом h , то задача (9.1) сводится к решению большого числа более простых задач.
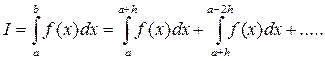 (9.2)
(9.2)
Для нахождения площади фигуры на шаге h будем аппроксимировать подинтегральную функцию. При аппроксимации функции только постоянной получим метод прямоугольников.
В методе левых прямоугольников для аппроксимации выбирается значения функции на левом конце участка h.
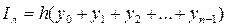 (9.3)
(9.3)
В методе правых прямоугольников для аппроксимации выбирается значения функции на правом конце участка h.
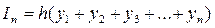 (9.4)
(9.4)
Точность метода прямоугольников можно оценить по разности (9.3) и (9.4)
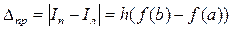 (9.5)
(9.5)
Погрешность метода прямоугольников пропорциональна первой степени шага h.
Если часть подинтегральной функции на шаге h аппроксимировать прямой линией , то площадь элементарного участка равна площади трапеции, а интеграл рассчитывается по формуле
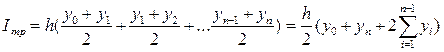 (9.6)
(9.6)
Формулу (9.6) называют формулой трапеций.
Её точность 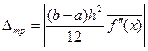 (9.7)
(9.7)
где 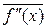 -среднее значение второй производной в интервале интегрирования. Точность метода трапеций пропорциональна квадрату шага h.
-среднее значение второй производной в интервале интегрирования. Точность метода трапеций пропорциональна квадрату шага h.
Если подинтегральную функцию аппроксимировать полиномом второго порядка (параболой), то можно получить, что 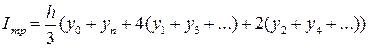 (9.8)
(9.8)
Формулу (9.8) называют формулой Симпсона.
Её точность
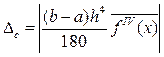 (9.9)
(9.9)
где 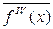 - среднее значение четвертой производной в интервале интегрирования. Точность метода Симпсона пропорциональна четвертой степени шага.
- среднее значение четвертой производной в интервале интегрирования. Точность метода Симпсона пропорциональна четвертой степени шага.
9.4 Порядок выполнения работы
- Получить задание для приближенного интегрирования дискретной и непрерывной функции.
- Сделать вручную расчет определенного интеграла для дискретно заданной функции по различным формулам приближенного интегрирования, приведенным в теоретической части и определить точность полученных результатов,
- Рассчитать при помощи автоматизированной системы различными методами для непрерывной функции приближенное значение определенного интеграла для различных значений шага, например 0.1,0.01,0.001 и т.д.
- Результаты расчетов с непрерывной функцией оформить в виде таблицы.
- Сравнить результаты приближенных расчетов с точным значением определенного интеграла , полученным аналитическим расчетом или
средствами автоматизированной системы с более высокой точностью.
- Построить графики зависимостей точности вычислений от шага.
Пример приближенного расчета определенного интеграла
Пусть требуется приближенно без применения автоматизированных систем определить значение определенного интеграла
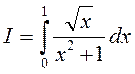
Будем делать расчет по формуле Симпсона (9.8). Сначала определим точность расчета для шага разбиения 0.25. Представим исходную функцию в виде таблицы соответствующих значений xi и yi и соответствующих им конечных разностей .
Таблица 9.2
| xi | yi | Δyi | Δ2yi | Δ3yi | Δ4yi |
| 0.00 | 0.000 | 0.471 | -0.375 | 0.269 | -0.205 |
| 0.25 | 0.471 | 0.095 | -0.107 | 0.064 | - |
| 0.50 | 0.566 | -0.011 | -0.043 | - | - |
| 0.75 | 0.554 | -0.054 | - | - | - |
| 1.00 | 0.500 | - | - | - | - |
Выбираем из таблицы 9.2 максимальное значение четвертой конечной разности и рассчитаем производную четвертого порядка
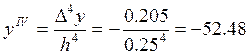
Ошибку рассчитаем по формуле (9.9) 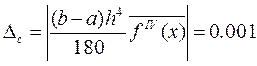
Для приближенного вычисления определенного интеграла используем формулу (9.8)
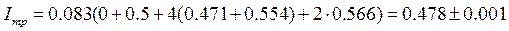
Приближенный расчет при помощи системы Mathcad
Дискретная функция задана вектором
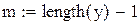 Число интервалов интегрирования Число интервалов интегрирования
|
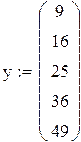
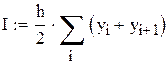 1. Интегрирование методом трапеций
1. Интегрирование методом трапеций
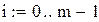
|
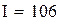
2.Интегрирование методом парабол ( Симпсона)
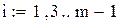
|
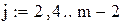
|
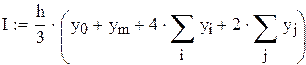
|
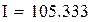
|
Прямое вычисление с помощью встроенной функции Mathcad
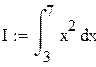
|
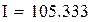
|
| <== предыдущая лекция | | | следующая лекция ==> |
| Антропогенный фактор как группа экологических факторов, возникшая вследствие человеческой деятельности. Его характеристика и влияние на живые системы | | | Свойства популяционной группы |
Дата добавления: 2016-08-08; просмотров: 1256;
