ПРОЦЕССЫ ПРЕОБРАЗОВАНИЯ И ВЫПОЛНЕНИЕ ПРОГРАММ

Декомпозиция

Языки программирования высокого уровня в значительной степени ориентированы на человеческий способ мышления. Алгоритмы, написанные на таких языках не понятны машинам. Их необходимо трансформировать в последовательность команд, которые будут вызываться соответствующие, вполне определенные, действия машины. Эта последовательность команд называется машинно-ориентированный язык. Характерным для этого языка является полное отсутствие сложных конструкций, например, таких как: разыменование, обобщенные виды, вызов процедуры, арифметические выражения с тремя и более действиями и т. д.

Формы машинно-ориентированного языка всегда элементарны. Допускаются:

1) обозначения, например: 10, ложь, «Иванов» и т.д.;

2) одноместные формулы, типа: 18 или (V) 20, sign a, abs b и т.д.;

3) двуместные формулы, например: 14+3, а*а, «Паро»+ «ход» и т.д.

Более сложные формулы нужно разлагать на элементарные, вводя вспомогательные обозначения для промежуточных результатов. Запись формул становится длиннее, а среднее количество информации, приходящейся на знак, уменьшается.

Продемонстрируем разложение (декомпозицию) выражение в «трехадресную форму» на примере:

х=(а*b+(а+d)*c)/(a*a+b*b)

h1=a; a

h2=b; b Один операнд (h2)

h1=a*b; x и одна переменная (h1)

h2=a; a

h3=d; d Один операнд (h3)

h2=h2+h3; + и одна переменная (h2)

h3=c; c

h2=h2*h3; x Два операнда (h3, h2)

h1=h1+h2; + и одна переменная (h1)

h2=a; a

h3=a; a Один операнд (h3)

h2=h2*h3; x и одна переменная (h2)

h3=b; b

h4=b; b Один операнд (h4)

h3=h3*h4; x и одна переменная (h3)

h2=h2+h3; +

h1=h1/h2; / Один операнд (h2) и одна

переменная (h1)

Замечание1.

Информация в правом столбце не имеет отношение к реализации схемы вычисления. Если этот правый столбец записать в строку с лево направо, то получим так называемую польскую инверсную запись (ПОЛИЗ) декомпонированной формулы.

Замечание 2.

В приведенном примере, первой становится свободной та переменная, куда значение было помещено последним (h4, h3, h2 и h1 – последовательность освобождения переменных). Память организованной по такому принципу называется магазином. После исполнения формулы, результат находится в первой переменной магазина h1 (и ни в какой другой – это контроль!).

Определение.

Трехадресная форма - это форма, в которой задаются, как максимум, два операнда иодна переменная для результата.

Поскольку промежуточный результат часто сразуже используется как операнд, целесообразно иметь специальную переменную, с которой осуществляются эти операции. Переменная предназначенная для накопления суммы, носит название сумматор (СМ) и имеет вид:

СМ=СМ+а.

Самостоятельно провести перевод в одноадрестную форму приведенную выше формулу, используя понятие сумматор.

Подсказка. Вначале необходимо каждую трехадрестную команду заменить тремя одноадрестными, а затем лишние команды вычеркнуть.

Замечанеи 3. Декомпозиция проводится нетолько арифметических выражений, но логических формул, операторов языка программирования массивов и подпрограмм с цель создания загрузочного модуля.

Адреса и ячейки

Определение. Имя – это ссылка на некоторые значения, точнее говоря. На другой объект, обладающий этим значением.

Пример:

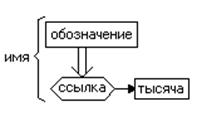Рис. Имена как специальные объекты ссылки.

Примечание:

- обозначает или одно и тоже;

- стрелка ссылки.

Определение. Генерируемые имена – это имена, выбираемые из бесконечного запаса имен.

Будем называть генерируемые имена адресами, если выполнены два условия, первое из которых представляет массив.

1. Адреса образуют неограниченное линейно упорядоченное счетное множество, изоморфное множеству натуральных чисел.

2. Адреса – это имена, не имеющие вида.

Точно так же как имя вместе со своим содержимым образует переменную, адрес вместе с со своим содержимым (содержимым ячейки) образует ячейку.

7011о 0.81134

адрес содержимое

ячейки

ссылка 0.81134

Рис. Ячейка.

Из сказанного следует, что адрес – это, фактически, новое имя обозначения, присвоенное системной программой языка программирования.

Обозначение адрес

Пример: Хº7011о; Х=0.81134

Новое имя «Х» есть номер адреса 7011о, по которому размещается значение 0.81134.

Примечание: Нулевой индекс «о» внизу номера обозначает адрес.

Полный список адресов и содержимым ячеек, называется памятью. Таким образом, память – это линейно упорядоченное множество переменных, последовательность ячеек.

Пример: х=5.3;

Цел. i

Массив к [1¸3]

Лог. m = (истина, ложь)

Компл. n.

Для машины получим

Таблица

идентификаторов

х 1043о 0.53

1044о 10Е1

i 1045o нет начальной загрузки (скип)

k 1046o не определено (нил)

1047o нил

1048o нил

m 1049o истина

1050o ложь

n 1051o нил

память

Для сближения трехадресной формы с одноадреспой, организации массивов, декомпозиции операторов цикла и организации вычислительного процесса используют индекс – регистр (ИР). ИР работает только с целыми числами по принципу сумматора (СМ). В нем предусмотрены четыре возможности счета:

ИР=ИР+1; ИР=ИР-1;

ИР=ИР+const; ИР=ИР-const.

Обычно имеется несколько индекс-регистров ИР1, ИР2,…, которые служат сумматорами адресного арифметического устройства. В дополнение к сказанному возможен обмен информацией между ИР и СМ.

Машина Тьюринга.

В 1930-х годах Алан Тьюринг и Алонза Черч предложили чрезвычайно простые модели вычисления и затем выдвинули утверждение: «Любое исполнимое вычисление может быть выполнено на любом из этих моделей.»

Оператор машины Тьюринга выполняется за четыре следующие шага:

1. Считать и проверить символ в текущей ячейке ленты.

2. Заменить символ на другой символ (необязательно).

3. Увеличить или уменьшить указатель текущей ячейки.

4. Перейти к другому оператору.

Согласно тезису Черча – Тьюринга, любое вычисление может быть запрограммировано на этой примитивной машине. Доказательство тезиса опирается на два утверждения:

- все существующие модели вычислений могут быть реализованы машиной Тьюринга;

- пока нет ни одного вычисления, которое не реализовано машиной Тьюринга.

Вывод. Так как машину Тьюринга легко смоделировать на любом языке программирования, можно сказать, что все языки программирования делают одно и то же.

Пример на С++. char tape […]; - лента tape бесконечна.

int current = 0;

L17: if (tape [current] == ‘g’){

tape [current++] = ‘j’; go to L43;}.

Примечание. сhar – tape имеет символьный тип;

int – current – имеет целый тип.

4.4. Общая структура программы в машинных кодах.

У разных вычислительных машин разный ассортимент выполняемых команд. Основными командами всех машин являются: арифметические команды, команды индексной арифметики и команды передачи управления. Команда состоит из адреса, количества используемых сумматоров, доначнительного разряда косвенной адресации и кода операции, конкретизирующего выполняемую операцию.

Программа в машинных кодах представляет из себя упорядоченную последовательность пронумерованных ячеек памяти. Память (программы) состоит из двух частей: рабочей и программной. Рабочая память предназначена для таблицы идентификаторов. В программной памяти размещаются команды для выполнения операций над величинами из рабочей памяти. Последовательность ячеек памяти – это чередование частей (кусков) рабочей и программной памяти. Для того чтобы перескочить через ячейки рабочей памяти, используются команды передачи управления. Таким образом, конец программной памяти предложения (куска) всегда конечен командой перехода.

В сложных программах с подпрограммами используют переход с возвратом. Переход с возвратом – это переход, использующий ячейку косвенной адресации, т.е. ячейку в которой хранится адрес точки возврата в основную программу.

Пример: 1о 10о

2о 11о

3о 12о

4о 13о

5о 14о

6о 5о 15о

7о Подпрограмма

8о

9о

Основная

программа

4о - ячейка, содержащая команду передачи управления;

15о - ячейка косвенной адресации памяти, т.е. ячейка 15о содержит адрес 5о возврата.

5о - ячейка точки возврата.

Замечание. Чтобы иметь возможность выполнять многократные переходы на подпрограммы, необходимо предусмотреть магазин ячеек косвенной адресации. Что уже относится к динамическим аспектам организации памяти.

4.5. Процесс выполнения программы в машинных кодах.

Основными устройствами вычислительной машины являются: исполнительное, запоминающее и управляющее. В управляющем устройстве содержится счетчик, в котором находится адрес команды, выполняемой следующей (счетчик команд – обозначен на рис.). Как уже говорилось, программа в машинных кодах – это упорядоченная последовательность адресов ячеек памяти. После исполнения любой команды (обозначим её адрес расположения через), не являющейся командой передачи управления, счетчик команд увеличивается на единицу и затем выполняется команда, имеющая адрес io+1. (См. рис. 1 и 2).

Исполнительно

устройство

Адресная Код

часть операции

Счетчик

Команд

Запоминающее

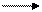
устройство

Рис. 1. Код операции – передача управления. Адресная часть не содержит ссылок на индекс-регистр и косвенную адресацию.

Адресное Исполнительное

арифметическое устройство

устройство

Адресная +UР Код

часть операции

Счетчик команд

Запоминающее

устройство

Рис. 2. Код операции – не передача управления. Адресная часть содержит ссылку на индекс – регитр.

Арифметические команды, содержащие адрес, осуществляются в два такта:

1. Управляющее устройство запускает процесс формирования адреса и его передачи в запоминающее устройство. На рис.1 и 2 представлены два метода (их гораздо больше) формирование адреса.

Первый метод (Рис. 1) – текущий адрес io получен из io-1 путем его увеличения на 1.

Второй метод (Рис.2) – текущей адрес получен:

а) из io – UР путем его увеличения на значение ИР. Этот метод используется, когда, например, необходимо перешагнуть через участок рабочей памяти основной программы.

Замечание 1. Здесь не идет речь о передачи управления. Передача управления производится только на подпрограмму (самостоятельный модуль).

б) io - результат косвенной адресации, т.е. io содержался в предыдущей команде. В этом случае адресная часть сразу передает io в запоминающее устройство (рисунок отсутствует ! См. книгу Ф. Бауэр и Г. Гооз).

2. Управляющее устройство на основании кода операции запускает исполнительное устройство, которое осуществляет необходимую переработку полученного из ячейки памяти запоминающего устройства (рис. 1, 2).

Действие команды передачи управления заключается в том, что значение счетчика команд устанавливается равным адресу, указанному в команде передачи управления (рис. 3).

Исполнительное

устройство

Адресная Код

часть операции

Счетчик команд

Запоминающее устройство

Рис. 3. Код операции – передача управления.

Замечание 2. После передачи управления процесс обработки программы продолжается либо, схемам представленным на рис. 1, 2, либо каким-то другим. Поэтому в данной схеме (рис. 3) не задействовано исполнительное устройство.

Управляющее устройство наряду со счетчиком команд содержит еще командный регистр, в котором располагается код команды.

Первые вычислительные машины (фон Нейман) не имели адресного арифметического устройства до тех пор, пока рабочая и программная память не были полностью отделены друг от друга (Эйкен). Включение адресных арифметических устройств в структуру вычислительной машины (Шехер) позволило учесть индексацию и наличие многих уровней имен.

Полная структурная схема процессов обработки программы в вычислительном устройстве изображена на рис. 4.

Адресное Исполнительное

арифметическое устройство

устройство

рим Адресная +UР Код

часть операции

+1

Счетчик команд

Управляющее устройство

Запоминающее устройство

Примечание. рим – оператор извлечения содержимого какого-либо объекта или оператор разыменования – уменьшает (разыменовывает) уровень объекта на единицу.

Пример 1. const int n или конст. цел. N

n=5

x=рим n

х – имеет целый тип и равно 5.

Пример 2. х=рим у+7

х- равно содержимому «у» +7.

Пример 3. к=рим 545о+9

к – есть сумма значения, расположенного по адресу 545о и 9.

Пример 4. io=рим 34o+UP

Содержимое ячейки 34о есть адрес – косвенная адресация.

4.6. Преобразование программы в машинные коды

В ЦП (центральном процессоре) находится набор регистров (специальных ячеек памяти), в которых выполняется вычисление, и указатель команды, который содержит номер следующей вызываемой ячейки памяти, где расположена очередная команда.

Во многих компьютерах, называемых Компьютерами с Сокращенной системой команд (RISC-Reduced Instruction Set Computers) для увеличения быстродействия используются только элементарные команды:

1. Доступ к памяти. Загрузить (load) содержимое слово памяти в регистр и сохранить (store) содержимое регистра в слове памяти.

2. Арифметические команды типа сложить (add) и вычесть (sub). Они выполняются над содержимым двух регистров или регистра и слова памяти. Результат остается в регистре. Например, команда

add R1, N

складывает содержимое слово памяти N с содержимым регистра R1 и оставляет результат в регистре.

3. Сравнить и перейти. ЦП может сравнить два значения, находящихся в регистрах и в зависимости от результата (равно, больше и т. д.) указатель команды изменяется. Например:

jump_ed R1, L1

…….

L1: …….

заставляет ЦП продолжать вычисление с команд с меткой L1, если R1=0 (ноль). В противном случае вычисление продолжается со следующей команды.

В компьютерах известных как CISC (Complex Instruction Set Computers) определен. Сложный набор команд, позволяющий упростить программирование на языке ассемблера и конструкцию компилятора.

Повторение. Память – это набор ячеек, в которых хранятся данные. Каждая ячейка памяти называется словом память и имеет адрес. Каждое слово память состоит из фиксированного числа битов: 16,32 или 64 битов. Современные ПК способны загружать и сохранять 8-битовые байты или двойные слова из 64 битов.

Примеры использования адресации в командах для С:

Пример 1. Способ непосредственной адресации, при которой операнд является частью команды. Значением операнда может быть адрес переменной (косвенная адресация):

load R2, #54 - загрузить значения 54 в регистр R2.

load R4, & N - загрузить адрес N в регистр R4.

Пример 2. Способ абсолютной адресации, в котором используется «символический» адрес переменной:

load R4, 43 -загрузить содержимое адреса 43 в R4.

load R3, I - загрузить содержимое переменной I в R3.

Пример 3. Использование индексных регистров. Индексные регистры не обязательно обособлены от регистров, используемых для вычислений.

load R2, 18 (R1) - загрузить в регистр R2 содержимое слова памяти, находящегося по адресу, равному сумме 18 и содержимому индексного регистра R1 (18+addr(R1), где addr(R1) - обозначение индексного регистра, скорее всего, даже суммы (add) индексного регистра (r))

add<-r=addr.

load R2, (R3) - загрузить содержимое addr(R3)+0 в R2 .Содержимое регистра R3 используется просто как адрес слова памяти, содержимое которого загружается в R2.

Пример 4. Использование команд при представлении выражения:

а*(b+с)

load R1, b

load R2, c

add R1, R2 – Сложить в ис. Результат занести в R1.

load R2, a

mult R1, R2 – Умножить а на b+c. Результат занести в R1.

Поскольку компьютеры – двоичные машины, распознающие только нули и единицы, то каждая команда, например, представленная в приведенных выше примерах, должна быть преобразована к двоичному цифровому виду. Одним из первых программных средств был символический ассемблер. Ассемблер берет программу, написанную на языке Ассемблера в символьном виде, и транслирует символы в двоичное представление, пригодное для выполнения на ПК.

V Автоматы и формальные языки

5.1. Обозначения

№	Символ	Значение символа	Примечание
		Не	Истина=ложь, ложь=истина
	^	И	Конъюнкция истина ложь истина истина ложь ложь ложь ложь
	V	Или	Дизъюнкция истина ложь истина истина истина ложь истина ложь
	∪	Или	Е1∪Е2-событие Е1, или Е2, или и то, и другое, не исключающее друг друга.
	∩	И	Е1∩Е2- событие Е1 и Е2
	~	Не	Ẽ- событие не Е
	⊂	Включение	Отношение [ превратилось в логическое отношение включения –С. Равенства А+В=В, или АВ=А эквивалентны отношению А[В или ВáА, что соответствует записи А⊂В или В⊃А.
	L		Логическая единица. L=истина
			Логический ноль. L=ложь
	∊	Принадлежит	А∊В- множество А ∊ множеству В
	\

Общепринятые уравнения:

- Т(Е1∪Е2)=Т(Е1)+Т(Е2);

- Т(Е1∩Е2)= Т(Е1)Т(Е2);

〜

- Т(Ẽ) =Т(Е).

Пусть задано некоторое множество М. Всякое множество ℛ пар (а,b) при а,b∊М называется отношением в М. Вместо (а,b)∊ ℛ

будем писать 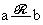.Отношение называется рефлексивным, если всегда 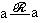; транзитивным, если пр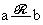и и 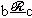всегда выполняется 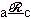; симметричным, если при 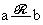всегда выполняется 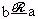; антисимметричным, если при a≠b соотношения 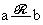и 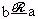никогда не выполняются одновременно

Рефлексивное, транзитивное и симметричное отношение называют отношением эквивалентности. Оно разбивает множество М на непересекающиеся классы эквивалентных элементов.

5.2. Автоматы

Пусть j - некоторое множество элементов, называемых состояниями, а g - некоторый набор знаков, называемый множеством входных символов. Для каждого состояния и каждого символа указано некоторое новое состояние, в которое переходит система.

d1

Обозначим это, как отображение d из j´g в g или j´g®j.

С алгебраической точки зрения речь идет о других множествах j и g со смешанной операцией tÎg, sÎj, tsÎj. Такая алгебраическая структура называется детерминированным автоматом А=(g,j).

Переключательные схемы (простейшие элементы ИС) являются системами с состояниями и переходами из одних состояний в другие. По сути, они представляют собой автомат, состояниями которого являются состояния переключательной схемы, а входными символами – комбинации значений на входе переключательной схемы.

Символическое изображение переключательного элемента:

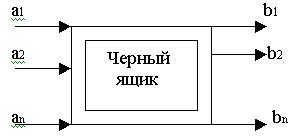
Входные параметры: а1, а2, а3, … аn.

Выходные параметры: b1, b2, b3 , … bn.

Причем b1=f1(а1, а2, а3, … аn),

b2 =f2(а1, а2, а3, … аn) и т.д.

5.3. Полугруппы, таблицы и диаграммы переходов

Под полугруппой понимают множество Y с некоторой операцией умножения – ◦, представленной в виде отображения:

◦

Y´Y®Y, которая (операция) ассоциативна:

"a, b, cÎY : a◦(b◦c)=(a◦b)◦c

Здесь приняты обозначения:

" - для всех

: - выполняется следующее.

Операцию над элементами конечного множества можно представить в виде таблицы:

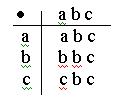
(5.1)

Диаграмма Кэли к таблице 5.1.

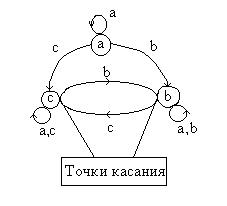
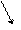ВходСостояние

a0 b = b

a0 a = a

Что не всякое отображение Y´Y®Y является ассоциативным, показывает следующий пример:

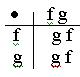
(5.2)

Следовательно (fg)f=ff=g,

f(gf)=fg=f.

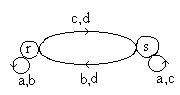
В виде таблицы переходов можно описать и автомат с конечным числом состояний и входных символов. Для автомата с двумя состояниями r и s и четырьмя входными символами а, b, c, d эта таблица может выглядеть так:

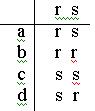
(5.3)

Диаграмма переходов к таблице 5.3.

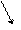ВходСостояние

c0 s = s

b0 r = r

Для описания операций можно воспользоваться диаграммой Кэли или диаграммой переходов автоматов. В обоих случаях речь идет ориентированных графах с помеченными дугами. Элементы полугруппы, заключенные в кружок, соответствуют состоянию автомата и выступают в роли вершин графа. Дуга с буквой «а» соответствует входным символам и ведет от одного состояния к другому.

5.4. Автоматы с выходом

Автомат с выходом есть некоторое множество σ выходных символов, образованных путем отображения λ из γ×φ.

λ

γ×φ→ σ (5.4)

Если выходной символ зависит от входного символа и состояния, то это автомат Мили (5.4.). Если выходной символ зависит только от состояния:

λ

φ→ σ , (5.5)

то говорят об автомате Мура.

Пусть автомат с входными символами {0,L}и состояниями {s1, s2, …s10}имеет диаграмму переходов:

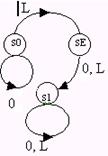
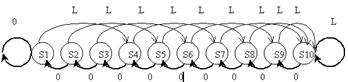
Из состояния s1 в состояние s10 можно попасть, подавая на вход слова:

LLL, LLLL, LLLLL, …

LLL0L, LL0L0L, …

0L0L0L0L, L00L00L00L00L00L00L, …

Этот автомат можно дополнить до автомата Мура, который, например, в состояниях s1, s2, … ,s9 будет выдавать символ «тихо», а в состоянии s10 – символ «звонок». А можно образовать автомат Мили, который дает звонок только тогда, когда состояние s10 достигается, например, при поступлении символа L на состояние s7, и никуда иначе.

5.5. Языки автоматов

Пусть в автомате A=(γ,φ) выделены два состояния: начальное – s0 и заключительное - sE . Говорят, что слово х=tktk-1 …t2t, допускается инициальным автоматом (a, s0, sE), если xs0=sE, т.е. если цепочка состояний s0, s1, … , sk, определяемая переходами

si+1=ti+1si (i=0,1, …, k-1) (5.6)

ведет к заключительному состоянию sk=sE.

Примеры автоматов с разным количеством допускаемых слов:

1. Автомат, воспринимающий одно единственное слово.

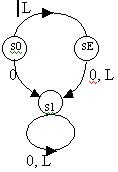Слово: L

S1=SE

В состояние S1, можно попасть, задав на входе S0 – 0 (S1 = 0S), но это состояние S1 не будет заключительным. Из состояния S1 попасть в SE невозможно!

2. Автомат, воспринимающий ровно два слова.

Два слова: 0 или L.

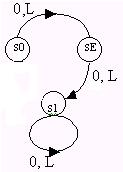
S1 = SE

В заключительное состояние SE можно попасть только из S0, задав слово 0 или L. Тогда согласно определению инициального автомата SE = S1 = t1S0 = (0VL)S0. Из состояния SE в S1 попасть можно, наоборот нет! Существует как бы два состояния S1, одно из которых является заключительным SE.

3. Автомат, воспринимающий бесконечное множество слов.

На начальное состояние S0 могут подаваться слова:

L, 0L, 00L, 000L, …

4. В приведенных выше трех примерах речь идет о конечных автоматах, названных так по причине конечного числа состояний. Приведем пример бесконечного автомата:

Все состояния автомата, за исключением конкретного S0 = SE, обозначим Si, где i – натуральное число и полагаем

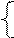LSi = SE, если i = -1,

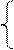Si+1 в остальных случаях, (5.6)

SE, если i = 1,

0Si = Si-1 в остальных случаях.

Словарный запас описывается выражением – допускается всякое слово, которое состоит из одинакового числа 0 и L. Образно говоря «откуда вышли, туда и пришли».

5. Автомат – дерево.

Для конечных автоматов диаграмму переходов можно изображать в виде дерева с корнем в начальном состоянии. При этом ветвь обрывается, когда достигается состояние, которое уже было. Покажем диаграмму переходов автомата в виде дерева на примере §5.4.

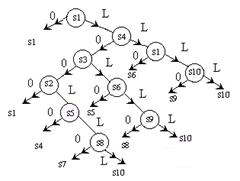
5.6. Формальные языки

5.6.1.Формальные системы

Отдельные автоматы, индуцируемые последовательностью

входных символов t1, t2, … tk, можно выполнить последовательно друг за другом. При этом совокупное отображение будет представлено словом над набором γ

tk tk-1 … t2t1 (5.7)

Таким образом,

tk tk-1 … t2t1s = tk(tk-1 … t2t1s). (5.8)

Сами отдельные символы – это однобуквенные слова. Множество всех слов бесконечно, даже в том случае, когда набор знаков конечен.

Для слов определена операция с символом «◦»-конкатенация:

(tl tl-1 … tk+1)◦(tktk-1 … t2t1) = tl tl-1 … tk+1 tk … t1 (5.9)

Ассоциативность конкатенации очевидна. Поэтому множество слов над набором знаков γ является полугруппой относительно конкатенации. Эта полугруппа обозначается через γ* и называется свободной полугруппой с множеством порождающих γ.

Для изложения идеи формальных систем изменим несколько следующие понятия и введем новые:

1. Множество γ будем называть набором терминальных символов.

2. Под состояниями будем понимать так же символы, которые назовем нетерминальными символами или синтаксическими переменными.

3. Множество β=γUφ назовем словарем.

4. Таблицу переходов заменим конечным множеством примитивных правил замены – правил вывода.

_ _

Вместо s=ts будем писать xs → xts, для произвольного xÎ γ*.

Направление стрелки – направление вывода, оно противоположно направлению перехода от одного состояния к другому. Например, a→ b означает, что «b» непосредственно выводимо из «a», т.е. «a» является предшественником «b».

a b ?!

_

Объяснение: а= s, b= ts. _

Получение s можно представить следующим образом:

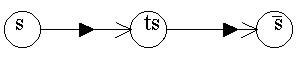
Образование слова производится по принципу от простого «s»

__

к сложному «ts»= «s». Именно об этом говорится в §5.5 при

__ __

определении инициального автомата. (s0=s, sE=ts,s1=s, s=sE)

5. Все, что можно вывести при помощи последовательности замен, указывается стрелкой =>, т.е. вместо

_

s= tk tk-1 … t2 t1s _

будем иметь xs=>x tk tk-1 … t2 t1 (5.9)

Обозначим множество выводов типа (5.9) β*.

6. Считаем, что слово xÎ γ* допускается, если хs0 выводимо

из sE: sE=> хs0 (5.10)

Заменим s0 на пустое слово ε, а sE – на символ z.

z =>x - означает «х допускается».

7. Пусть a, b, c слова из β*. Если b => и c=>b, то c=>a. Иначе говоря, отношение => транзитивно.

Формальной системой Σ = (β,=>,z) называется свободная полугруппа β* слов над β вместе с заданным на ней транзитивным отношением =>, называемым синтаксисом или структурой вывода, и аксиомой zÎ β.

Если выполнено соотношение a=>b, то выводимо из а. Множество всех слов, выводимых из z, называют ядром формальной системы.

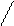Формальная грамматика Г= (β,γ,=>,z), где γcβ и zÎγ – это формальная система (β,=>,z), синтаксис которой предназначен для выделения в ядре всех тех слов, которые состоят только из терминальных символов.

Словарным запасом или языком z(Г), порождаемым грамматикой Г- множество всех слов из γ*, выводимых из z через отношения =>.

Словарный запас вместе с синтаксисом, позволяющим выводить из z отдельные слова, составляет формальный язык Λ=(Г,Z(Г)), описываемый формальной грамматикой.

Ядро формального языка содержит множество всех слов, которые встречаются в выводах слов из словарного запаса.

Всякое конечное множество x1, x2,…, xn слов xi над набором символов γ можно рассматривать как формальный язык. При этом β = γU{z}, а отношение => представляет собой перечень слов из словарного запаса: z=>x1,

z=>x2,

z=>xn. (5.11)

5.6.2. Полутуэвские языки

Языки, в которых отношение →(с.б.) строится по более простому отношению →(с.м.), такому, что a→b (с.м.) (a,bÎβ*) ведет к xay→xby для произвольных х, уÎ β*. При этом говорят, что отношение вывода →(с.б.) является полугрупповым замыканием отношения вывода → (с.м.).

Рассмотрим пример. Пусть β={I}, β*={ε, I, II, III, …}так что β*\{ε}– это представление натуральных чисел ( \ - означает без). Пусть соотношение a=>b (a,bÎβ*) выполняется тогда, когда натуральное число, соответствующее а, меньше числа, соответствующего b. Диаграммой Хассе этого отношения будет:

(с.б) ε→I→II→III→… (5.12)

Граф отношения →(с.б.), порождающего отношение =>, называется диаграммой Хассе.

поскольку β* бесконечно, для всякого отношения, распространяющегося на бесконечное число слов из β*, неосуществимо перечисление соотношений даже для упрощенного отношения →.

Если в диаграмме Хассе (5.12) задать граф ε→I (с.м.), то

а.) при х1 = у1 = ε и а = ε, b = I, следует (с.б.) x1ay1→x1by1 =

= εаε →εbε = εεε→εIε или ε→I

б.) при х2=ε, у2=I и b=II следует (с.б.) х2 bу2 =εIII, но εIIε→ εIII, εIIε= x1IIy1, но из а.) =>, что x1ay1→x1by1 или x1εy1→x1IIy1= x1Iy1→x1IIy1, т.е. I=II (5.13)

в.) при х3=I, y3=II и b= II следует (с.б.).

х3by3 = IIIII, но εIIIε→ IIIII, εIIIε = x1IIIy1. Далее читаем в обратном порядке εаε →εIε→ εIIε→ εIIIε

εаε → εIIIε, но εаε = εIε→ εIIε→ εIIIε и т.д.

Вывод1 Очевидно, что теперь возможно с помощью конечного отношения →(с.м.) (в примере ε →I), т.е. отношения, которое перечислимо конечным числом пар соотношений, породить бесконечное отношение →(с.б.) как полугрупповое замыкание отношения →(с.м.).

Фактически из конечного числа пар xi, yi можно образовать бесконечное множество( в примере – это IIII …).

Определение1 Формальная грамматика называется полутуэвской, если отношение => является транзитивным замыканием полугруппового замыкания некоторого конечного отношения →(с.м.) на β*.

Определение2 Если соотношение а =>b можно получить с помощью конечного числа соотношений а→с1, с1→с2, с2→с3, …, сn→b, то говорят, что отношение →(с.б.) порождает => и называют отношение => транзитивным замыканием →(с.б.).

Определение3 Каждое соотношение называется продукцией языка.

Определение4 Язык порождаемый полутуэвской формальной грамматикой называется полутуэвским языком. В случае когда не учитывается разбиение β на терминальные и нетерминальные символы, говорят о полутуэвской системе.

Вывод2 Если в полутуэвской системе «b» выводимо из «а», то для "x, yÎβ* xby выводимо из xay. Замену a→b (с.м.) можно применять не только к полному слову «а», но и к каждому подслову «а» внутри любого слова «xay».

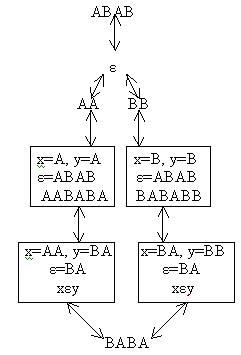
Пример к выводу 2 Пусть β состоит из двух элементов, т.е. β={A, B}. Продукциями являются:

ε →AA,

AA→ ε,

ε→BB,

BB→ ε ,

ε →ABAB,

ABAB →ε.

Элементом множества продукций этой системы можно представить графом:

5.6.3. Языки Хомского

Лингвист Ноэм Хомский в1955 г. ввел ограничение в полутуэвские системы: «Не допускается таких продукций, которые заменили бы слово, состоящее только из терминальных символов, на какое–нибудь другое слово».