Пересечение поверхностей геометрических тел

Плоскостями.

Сечение гранных тел плоскостью общего положения

Плоскость задана пересекающимися прямыми (горизонталью и фронталью).

Геометрическое тело - трехгранная призма.

А2

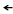
f 2 С2

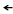
H 2 В2

1 2

Х1,2

f 1

1 1 3 1

h1 2 1

А1

С1

В 1 3 4

1 4

В 4

Х 1,4 А4 C4

Построить фигуру сечения можно используя различные, уже известные нам методы. Применим метод замены плоскостей проекций.

Выберем новую ось Х1,4 так, чтобы она была перпендикулярна к горизонтальной проекции горизонтали. Тогда горизонталь на плоскость П4 спроектируется в точку, а плоскость заданная горизонталью и фронталью - в линию( т.е. займет проецирующее положение).

Построим на плоскости П4 проекцию призмы. Вспомним порядок построения на примере точки 1 принадлежащей призме.

От проекции 11 проведем линию проекционной связи перпендикулярно оси Х 1,4. Циркулем замерим расстояние от оси Х1,2 до проекции точки 1 2 и отложим равное ему расстояние по линии проекционной связи от оси Х 1,4. Получим положение проекции точки

1 4 . После построения проекции призмы на плоскость П4, отметим точками А4 В4 С4 фигуру сечения призмы плоскостью. Эта фигура здесь очевидна, так как мы помним свойство проецирующих плоскостей. Теперь, чтобы получить фигуру сечения на плоскости П 1 и П 2 необходимо по линиям проекционной связи спроектировать точки АВС на соответствующие проекции ребер призмы.

Если перед нами стоит задача получить натуральную величину фигуры сечения , то мы можем сделать еще одну замену плоскости проекций , когда ось Х 4,5 пройдет параллельно проекции А4 В4 С4.

Можно использовать метод плоскопараллельного переноса или повернуть вокруг оси перпендикулярной плоскости П4 так, чтобы фигура сечения стала параллельна горизонтальной плоскости проекций. Для это надо вспомнить прошлую лекцию.