Разработка экспертной системы в программе Mini Expert System.
Программа Mini Expert System представляет собой простую экспертную систему, использующую байесовскую систему логического вывода. Она предназначена для проведения консультации с пользователем в какой-либо прикладной области (на которую настроена загруженная база знаний) с целью определения вероятностей возможных исходов и использует для этого оценку правдоподобности некоторых предпосылок, получаемую от пользователя.
На первом этапе создания базы знаний необходимо сформулировать знания о рассматриваемой области в виде двух наборов: Q = {qj} – набор вопросов (симптомов, свидетельств) и V = {vi} - набор вариантов исхода (вариантов решения), а также двух матриц вероятностей: Py = {pyij} и Pn = {pnij} размером m´n, где pyij – вероятность получения положительного ответа на j-й вопрос, если i-й исход верен; pnij – вероятность получения отрицательного ответа на j-й вопрос, если i-й исход верен; n и m – количества вопросов и исходов соответственно. Кроме того, каждому исходу ставится в соответствие априорная вероятность данного исхода Р, т.е. вероятность исхода в случае отсутствия дополнительной информации.
В процессе работы ЭС решатель, пользуясь данными наборами и матрицами и теоремой Байеса, определяет апостериорную вероятность каждого исхода, то есть вероятность, скорректированную в соответствии с ответом пользователя на каждый вопрос:
- при положительном ответе 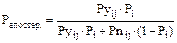 ,
,
- при отрицательном ответе 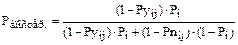 ,
,
- при ответе «не знаю» апостериорная вероятность равна априорной.
То есть вероятность осуществления некой гипотезы при наличии определенных подтверждающих свидетельств вычисляется на основе априорной вероятности этой гипотезы без подтверждающих свидетельств и вероятностей осуществления свидетельств при условиях, что гипотеза верна или неверна.
Исходная информация оформляется в виде текстового файла с расширением .DAT со следующей структурой:
Описание базы знаний, имя автора, комментарий и т.д.
(можно в несколько строк; эта информация выводится после загрузки базы знаний; данная секция заканчивается после первой пустой строки)
Вопрос № 0 (любой текст, заканчивающийся переносом строки)
Вопрос № 1
Вопрос № 2
...
Вопрос № N (после последнего вопроса следует одна пустая строка, и вторая секция заканчивается)
Исход № 0, P [ , i, Py, Pn ]
Исход № 1, P [ , i, Py, Pn ]
Исход № 2, P [ , i, Py, Pn ]
...
Исход № M, P [ , i, Py, Pn ]
| |
В начале описания правила вывода задаётся исход, вероятность которого меняется в соответствии с данным правилом. Это текст, включающий любые символы, кроме запятых. После запятой указывается априорная вероятность данного исхода P. После этого через запятую идёт ряд повторяющихся полей из трёх элементов. Первый элемент i – номер соответствующего вопроса. Следующие два элемента Pyij и Pnij – соответственно вероятности получения ответа «Да» на этот вопрос, если возможный исход верен и неверен. Эти данные указываются для каждого вопроса, связанного с данным исходом.
Примечание: P <= 0.00001 считается равной нулю, а P >= 0.99999 – единице, поэтому не следует указывать такие значения – исход с подобной априорной вероятностью обрабатываться не будет.
Например:
Грипп, 0.01, 1,0.9,0.01, 2,1,0.01, 3,0,0.01
Здесь сказано: существует априорная вероятность P = 0,01 того, что любой наугад взятый человек болеет гриппом.
Первому вопросу (i = 1) соответствует запись «1,0.9,0.01». Отсюда следуют значения Pyi1 = 0,9 и Pni1 = 0,01, которые означают, что если у пациента грипп, то он в девяти случаях из десяти ответит «Да» на этот вопрос, а если у него нет гриппа, он ответит «Да» лишь в одном случае из ста (т.е. данный симптом встречается довольно редко при других болезнях). Ответ «Да» подтверждает гипотезу о том, что у него грипп. Ответ «Нет» позволяет предположить, что человек гриппом не болеет.
При положительном ответе «Да» (+5) на первый вопрос апостериорная вероятность для рассматриваемого примера составит:
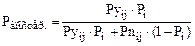 =
= 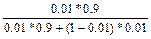 = 0,47619.
= 0,47619.
При отрицательном ответе «Нет» (-5) на первый вопрос апостериорная вероятность для рассматриваемого примера составит:
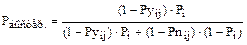 =
=
| |
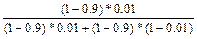 = 0,00102.
= 0,00102.
При ответе «Не знаю» (0) апостериорная вероятность исхода равна априорной: 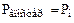 .
.
При промежуточном ответе h (от -5 до 0 и от 0 до +5) апостериорная вероятность рассчитывается с учетом степени уверенности принадлежности признака и рассчитывается линейной интерполяцией от значений утвердительных ответов «Да», «Нет», «Не знаю».
При отрицательном ответе (-5;0):
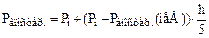 .
.
Например, при ответе h = -3:
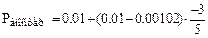 = 0,00461.
= 0,00461.
При отрицательном ответе (0;+5):
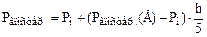 .
.
Например, при ответе h = +3:
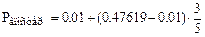 = 0,28971.
= 0,28971.
Для второго вопроса имеем запись «2,1,0.01». То есть, если у человека грипп, то этот симптом обязательно должен присутствовать (Pyi2 = 1) и он обязательно ответит «Да». Соответствующий симптом может иметь место и при отсутствии гриппа (Pni2 = 0,01), но это маловероятно.
Примечание: При большом количестве вопросов нет необходимости в каждой строке последней секции перечислять их все, тем более если ответ на какой-либо вопрос не влияет на вероятность данного исхода.
Дата добавления: 2016-05-05; просмотров: 1977;
