Ламинарное движение жидкости в цилиндрическом трубопроводе.

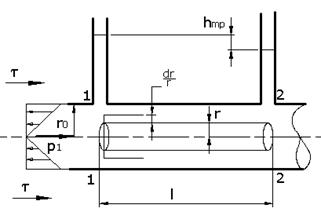
Рассмотрим ламинарное движение жидкости в горизонтально расположенном цилиндрическим трубопроводе, что исключить влияние сил тяжести.

Запишем уравнение Бернулли.

,

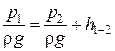
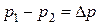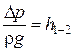
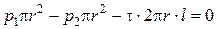– уравнение равномерного движения жидкости.

,

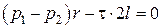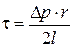
Согласно гипотезе Ньютона, экспериментально подтвержденной Петровым, при движении вязкой жидкости возникают касательные напряжения.

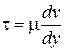
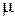– динамический коэффициент вязкости

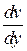– поперечный градиент скорости

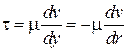
Знак "–" обусловлен тем, что отсчет 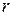происходит в обратном направлении от оси к стенке.

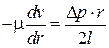
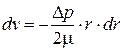
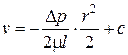
При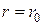

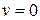
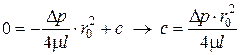
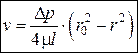– параболический закон Стокса

при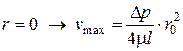

Найдем величину расхода через живое сечение. Для этого выделим слой жидкости размером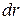

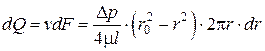
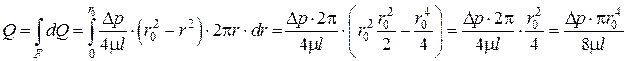
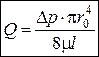– формула Пуазейля

Из уравнения Пуазейля найдем величину средней скорости:

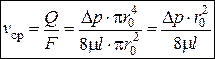
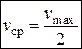
Найдем величину потери на трение.

Из уравнения Бернулли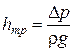

Величину 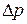выразим через :

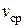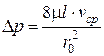
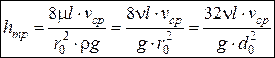– формула Пуазейля

Потери на трение при ламинарном движении зависят от скорости в первой степени.

Величину 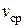выразим через :

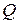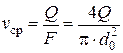
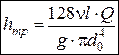– формула Пуазейля.

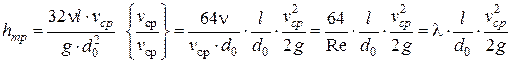
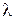– коэффициент сопротивления трения.

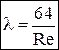– для ламинарного течения.

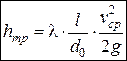– формула Вейсбаха

Квадрат скорости получен искусственным путем. В действительности потери зависят от скорости в первой степени.

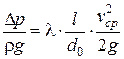
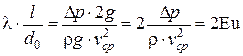
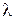можно рассматривать как критерий подобия .

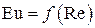Найдем величину коэффициента кинетической энергии при ламинарном движении:

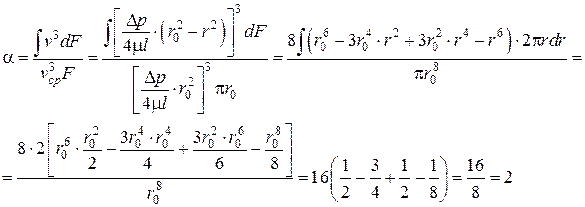
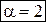– при ламинарном движении.