Динамические характеристики систем управления
Характеристики которые оценивают динамические свойства системы должны удовлетворять определенным требованиям:
1. Должны быть специфичны (система стабилизации).Задача которой состоит в поддержании на определенном уровне или регулирование выходной величины в определенных пределах
2. Характеристики должны быть достаточно точными. За установившейся режим можно принять такой режим, при котором ошибка системы, т.е. разность между требуемым и фактическим значениями управляемых величин постоянны во времени.
Работу системы в динамическом режиме можно описать используя дифференциальные уравнения.
Для последнего изображения динамики существует переходная характеристика динамики.
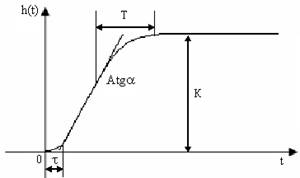 Т – постоянная времени, показывает инерционность. Определяется скоростью с которой выходная величина стремится к установившемуся значению;
Т – постоянная времени, показывает инерционность. Определяется скоростью с которой выходная величина стремится к установившемуся значению;

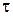 - запаздывание, связано с внутренним состоянием объекта, элемента и внешними взаимодействиями; К – коэффициент передачи; ∆-функция; h(t)-реакция звена на единичное ступенчатое воздействие.
- запаздывание, связано с внутренним состоянием объекта, элемента и внешними взаимодействиями; К – коэффициент передачи; ∆-функция; h(t)-реакция звена на единичное ступенчатое воздействие.
Рассмотрим реакцию САУ на единичном воздействии. Получим переходную функцию h(t) (классическая характеристика).
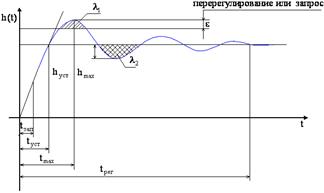
Можем найти основные показатели качества.
Параметры качества:
1. 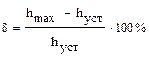 - перерегулирование
- перерегулирование
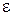 - коэффициент демфирирования диапазон регулирования
- коэффициент демфирирования диапазон регулирования
2. tрег – время регулирования. Необходимо, чтобы tрег было минимальным tрег=(3…4)∙Т
3. tзап – время запаздывания. При оптимальном выражении tзап=1/2∙tуст
4 Процесс затухания. Затухание процесса происходит по закону 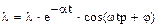 , где
, где 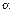 - логарифмический дикримент затухания:
- логарифмический дикримент затухания: 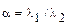
Оптимальный процесс происходит за три колебания.
Первые три показателя определяют зону, ограничивающую рассогласование системы в ходе процесса управления, т.е. чтобы оценить управление по этим показателям необходимо построить или экспериментально зарегистрировать эти показатели.
1. Представить методику расчета надежности невосстанавливаемой системы без резервирования (вероятность безотказной работы – случайная величина).
Ответ:
В теории надежности принято системы без резервирования изображать последовательно соединенными блоками.

Последовательность не связана с характером прохождения сигнала. Она свидетельствует о том, что система представляет собой цепочку блоков. Выход одного элемента цепочки приводит к отказу системы.
Обазначим состояние каждого блока таким образом:
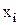 - i-ый блок исправен
- i-ый блок исправен
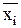 - i-ый блок не исправен.
- i-ый блок не исправен.
Расчет сводится к оценке исправности системы в зависимости от исправных состояний отдельных блоков. Необходимо найти вероятность безотказной работы отдельных блоков. Делается это так:
а) формулируется логическое высказывание, описывающие условие нахождения системы в исправном состоянии в зависимости от исправного состояния блоков
х1*х2*х3*…..*хn – это конъюкция;
б) находится вероятность безотказной работы системы как вероятность конъюкции Р1
Р=Р1(х1*х2*х3*…..*хn)
Отказы отдельных блоков могут быть зависимыми и независимыми друг от друга. В случае зависимых отказов вероятность безотказной работы системы такова:
Р=Р1(х1)*Р2(х2|х1)*Р3(х3|х2*х1)*…..*Рn(хn|x1*x2*…..xn-1), где Р1, Р2,….. Рn – вероятности безотказной работы соответствующих блоков.
В цифровой схемотехнике отказы отдельных элементов независимы друг от друга. В случае независимости отказов вероятность безотказной работы системы равна:
Р=Р1(х1)*Р2(х2)*….Рn(xn), где Р1(х1), Р2(х2),….Рn(xn) – вероятности безотказной работы соответствующих блоков.
Вероятность безотказной работы системы всегда меньше вероятности безотказной работы любого из блоков. Для того чтобы обеспечить более высокую надежность системы необходимо использовать более надежные элементы.
Очень часто требуется дать оценку максимальной вероятности безотказной работы системы, даже не прибегая к расчету.
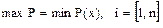
3. На испытания, было поставлено Nо=1000 однотипных полупроводниковых приборов. Через каждые 1000 ч работы учитывалось количество отказавших приборов. Испытание продолжалось до тех пор, пока не отказали все приборы. В таблице представлена выборка результатов испытаний полупроводниковых приборов на надежность.
Таблица
| Δt, ч | n(Δt) | Δt, ч | n(Δt) |
| 0-1000 | 9000-10000 | ||
| 1000-2000 | 10000-11000 | ||
| ….. | ….. | …... | …… |
| 7000-8000 | 25000-26000 |
Используя данные таблицы, рассчитать:
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Состояние электронов в атоме. Строение атомов элементов больших и малых периодов. |
Дата добавления: 2016-05-05; просмотров: 1299;
