Основные направления исследования эволюции систем
При исследовании эволюции системы необходима ее декомпозиция на подсистемы с целью обеспечения:
· эффективного взаимодействия с окружением;
· оптимального обмена определяющими материальными, энергетическими, информационными, организационными ресурсами с подсистемами;
· эволюции системы в условиях динамической смены и переупорядочивания целей, структурной активности и сложности системы;
· управляемости системы, идентификации управляющей подсистемы и эффективных связей с подсистемами, обратной связи.
Пусть имеется некоторая система S с N подсистемами. Для каждой i - й подсистемы определим вектор x(i) = (x1(i), x2(i),…,xni(i)) основных параметров, без которых нельзя описать и изучить функционирование подсистемы в соответствии с целями и доступными ресурсами системы. Введем в рассмотрение функцию s(i) = s(x(i)), которую назовем функцией активности или просто активностью этой подсистемы. Например, в бизнес-процессах это понятие близко к понятию деловой активности.
Для всей системы определены вектор состояния системы x и активность системы s(x), а также понятие общего потенциала системы.
Например, потенциал активности может быть определен с помощью интеграла от активности на задаваемом временном промежутке моделирования.
Эти функции отражают интенсивность процессов, как в подсистемах, так и в системе в целом.
Важными для задач моделирования являются три значения
s(i)max, s(i)min, s(i)opt
- максимальные, минимальные и оптимальные значения активности i - й подсистемы, а также аналогичные значения для всей системы (smax, smin, sopt).
Если дана открытая экономическая система (процесс), а Н0, Н1 - энтропия системы в начальном и конечном состояниях процесса, то мера информации определяется как разность вида:
ΔН = Н0 - Н1.
Уменьшение ΔН свидетельствует о приближении системы к состоянию статического равновесия (при доступных ресурсах), а увеличение - об удалении. Величина ΔН - количество информации, необходимой для перехода от одного уровня организации системы к другой (при ΔН > 0 - более высокой, при ΔН < 0 - более низкой организации).
Рассмотрим подход и с использованием меры по Н. Моисееву.
Пусть дана некоторая управляемая система, о состояниях которой известны лишь некоторые оценки - нижняя smin и верхняя smax. Известна целевая функция управления
F(s(t), u(t)),
где s(t) - состояние системы в момент времени t, а u(t) - управление из некоторого множества допустимых управлений, причем считаем, что достижимо uopt - некоторое оптимальное управление в пространстве U, t0 < t < T, smin  s
s  smax.
smax.
Мера успешности принятия решения может быть выражена математически:
H = |(Fmax - Fmin) / (Fmax + Fmin)|,
Fmax = max F(uopt, smax), Fmin = min F(uopt, smin),
t  [t0;T ], s
[t0;T ], s  [smin; smax].
[smin; smax].
Увеличение Н свидетельствует об успешности управления системой .
Функции должны отражать эволюцию системы, в частности, удовлетворять условиям:
1. Периодичности (цикличности), например:
(  0 < T < ∞,
0 < T < ∞,  t:
t:  (i)(s; s(i), t) =
(i)(s; s(i), t) =  (i)(s; s(i), t + T),
(i)(s; s(i), t + T),
 (i)(s; s(i), t) =
(i)(s; s(i), t) =  (i)(s; s(i), t + T)).
(i)(s; s(i), t + T)).
2. Затуханию при снижении активности, например:
(s(x)  0
0  i = 1, 2, ..., n) => (
i = 1, 2, ..., n) => (  (i)
(i)  0,
0,  (i)
(i)  0).
0).
3. Стационарности: выбор или определение функции  (i),
(i),  (i) осуществляется таким образом, чтобы система имела точки равновесного состояния, а s(i)opt, sopt достигались бы в стационарных точках x(i)opt, xopt для малых промежутков времени. В больших промежутках времени система может вести себя хаотично, самопроизвольно порождая регулярные, упорядоченные, циклические взаимодействия (детерминированный хаос).
(i) осуществляется таким образом, чтобы система имела точки равновесного состояния, а s(i)opt, sopt достигались бы в стационарных точках x(i)opt, xopt для малых промежутков времени. В больших промежутках времени система может вести себя хаотично, самопроизвольно порождая регулярные, упорядоченные, циклические взаимодействия (детерминированный хаос).
Взаимные активности  (ij)(s; s(i), s(j), t) подсистем i и j не учитываются. В качестве функции
(ij)(s; s(i), s(j), t) подсистем i и j не учитываются. В качестве функции  (i),
(i),  (i) могут быть эффективно использованы производственные функции типа Кобба - Дугласа:
(i) могут быть эффективно использованы производственные функции типа Кобба - Дугласа:
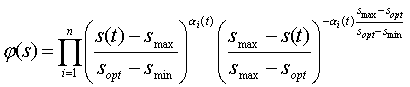
В таких функциях важен параметр  i, отражающий степень саморегуляции, адаптации системы. Как правило, его нужно идентифицировать.
i, отражающий степень саморегуляции, адаптации системы. Как правило, его нужно идентифицировать.
Функционирование системы удовлетворяет на каждом временном интервале (t; t + τ) ограничениям вида
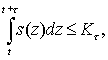
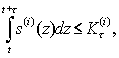
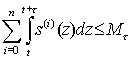
При этом отметим, что выполнение для τ > 0 одного из двух условий
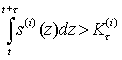
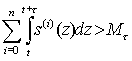
приводит к разрушению (катастрофе) системы.
Обратимся к социально - экономической среде, которая может возобновлять с коэффициентом возобновления
 (τ, t, x) (0 < t <T, 0 < x < 1, 0 < τ < T)
(τ, t, x) (0 < t <T, 0 < x < 1, 0 < τ < T)
свои ресурсы. Этот коэффициент зависит, в общем случае, от мощности среды (ресурсоемкости и ресурсообеспеченности).
Рассмотрим простую гипотезу:
 (τ, t, x) =
(τ, t, x) =  0 +
0 +  1x,
1x,
Чем больше ресурсов - тем больше темп их возобновления. Запишем непрерывную эволюционную модель, где a - коэффициент естественного прироста ресурсов, b - убыли ресурсов:
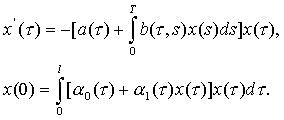
Пусть  (τ) =
(τ) =  0(τ) +
0(τ) +  1(τ) x(τ) > 0. Тогда
1(τ) x(τ) > 0. Тогда
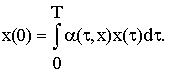
Задача всегда имеет решение при x = 0. Тогда эволюционный потенциал системы можно определить как величину:
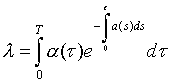
Чем выше темп возобновления  - тем выше λ, чем меньше
- тем выше λ, чем меньше  - тем ниже λ.
- тем ниже λ.
Напрашивается вывод. Каким бы хорошим ни было состояние ресурсов в начальный момент, они неизменно будут истощаться, если потенциал системы меньше 1.
Отметим, что если ds/dt - общее изменение энтропии системы, ds1/dt - изменение энтропии за счет необратимых изменений структуры, потоков внутри системы, ds2/dt - изменение энтропии за счет усилий по улучшению обстановки (например, экономической, экологической, социальной), то справедливо уравнение И. Пригожина:
ds/dt = ds1/dt + ds2/dt.
При эволюционном моделировании социально - экономических систем полезно использовать и классические математические модели и неклассические, в частности, учитывающие пространственную структуру системы, структуру и иерархию подсистем (графы, структуры данных и др.), опыт и интуицию (эвристические, экспертные процедуры).
Пример. Пусть дана некоторая экологическая система Ω, в которой имеются точки загрязнения (выбросов загрязнителей) xi, i = 1, 2, …, n. Каждый загрязнитель xi загрязняет последовательно экосистему в промежутке времени [ti-1; ti]. Каждый загрязнитель может оказать воздействие на активность другого загрязнителя (например, уменьшить, нейтрализовать или усилить по известному эффекту суммирования воздействия загрязнителей). Силу (меру) такого влияния можно определить через rij,
R = {rij: i = 1, 2,…, n-1; j = 2, 3,…, n}.
Структура задаётся графом: вершины - загрязнители, ребра – меры загрязнения. Найдём подстановку, минимизирующую функционал вида:
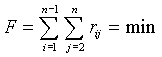
где F - суммарное загрязнение системы с данной структурой S.
Чем быстрее будет произведен учёт загрязнения в точке xi, тем быстрее осуществимы социально - экономические мероприятия по его нейтрализации. Чем меньше будет загрязнителей до загрязнителя xi, тем меньше будет загрязнение среды.
В качестве меры rij может быть взята мера, учитывающая как время начала воздействия загрязнителей, так и число, и интенсивность этих загрязнителей:
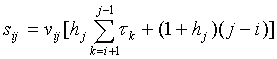
где vij - весовой коэффициент, определяющий степень влияния загрязнителя xi на загрязнитель xj (эффект суммирования), hj - весовой коэффициент, учитывающий удельную интенсивность действия загрязнителя xj и интервал τi, в течение которого уменьшается интенсивность (концентрация) загрязнителя. Весовые коэффициенты устанавливаются экспертно или экспериментально.
Принцип эволюционного моделирования предполагает необходимость и эффективность использования методов и технологии искусственного интеллекта, в частности, экспертных систем.
Адекватным средством реализации процедур эволюционного моделирования являются генетические алгоритмы.
Дата добавления: 2016-06-24; просмотров: 469;
