Отношение несовместимости.

2. Противоречащими (контрадикторными) являются сужде­ния А и О, Е и I, которые одновременно не могут быть ни истин­ными, ни ложными.

Hесовместимые единичные суждения могут находиться лишь в отношении противоречия и не могут находиться в отношении противоположности, ибо каждому от­дельному предмету может быть либо присущ, либо не присущ оп­ределенный признак.

14. Модальность суждений и ее виды: эпистемическая, деонтическая, алетическая.

Модальность – это определенным образом выраженное суждение, дополнительная хар-ка явлений их св-в и отношений между ними. Это хар-ка не воспринимается как четкая и однозначная информ. Более того, не всегда можно определить истина она или ложна.

Различаю 3 вида модальности:

1) Алетическая модальность выражается в терминах: необходимо, возможно, случайно (эти понятия называют операторами).

2) Эпистимическая – позволяет разделить суждения на 2 группы: достоверные (операторы: доказано и опровергнуто) и проблематичные (оператор: вероятно).

3) Деонтическая – используются операторы: обязательно, разрешено.

С точки зрения модальности, т.е. оценки отношения субъекта и предиката, суждения подразделяются на проблематические (вероятностные), ассерторические (утверждающие) и аподиктические (суждения долженствования).
1. Проблематические суждения содержат утверждения о предполагаемом отношении субъекта к предикату: Земля вероятно вращается вокруг Солнца.

2. Ассерторические суждения содержат утверждение о действительном отношении субъекта к предикату: Земля вращается вокруг Солнца.

3. Аподиктические суждения содержат утверждение о необходимости отношения субъекта к предикату: треугольник не может иметь сумму углов, большую 180°.

Модальный оператор - лингвистический термин для обозначения слов, в которых выражаются правила или возможности, например, "следует" и "не следует", "могу" и "не могу".

15. Логика высказываний (язык: алфавит, понятие формулы). Табличное определение логических связок.

Основные синтаксические категории языка логики высказываний, из которых должны строиться высказывания и высказывательные формы, называемые формулами языка логики высказываний, перечень знаков этих категорий называют исходными символами или алфавитом языка.

Алфавит логики высказываний:

1. Пропозициональные переменные p, q, r, s, а также эти же символы с числовыми индексами: p1, p2, … pn, …

2. Логические константы (связки): & (конъюнкция), 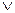(дизъюнкция), (импликация), 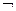(отрицание);

3. Технические знаки: ( – левая скобка, ) – правая скобка.

Формула – это осмысленное выражение логики высказываний.

Формулы логики высказываний:

1. Любая пропозициональная переменная (например, p, q, r, s) есть уже формула.

2. Если А и В – формулы, то (А & B), (A 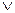B), (А 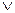В), (A B), (А 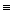В) тоже являются формулами.

3. Если А – формула, то 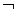А – формула.

4. Ничто иное не есть формула.

Табличное определение логических связок.

Знак	Название	Соответст. в рус. языке
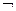
	отрицание	«не», «неверно, что»
&	конъюнкция	«и», «а», «но»
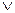
	дизъюнкция	«или»
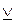
	строгая дизъюнкция	«или…или», «либо…либо»
	импликация	«если…, то…», «когда…, то…»
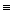
	эквиваленция	«если и только если», «тогда и только тогда»