Математическая постановка оптимизационной задачи
1. Дать словесную формулировку задачи.
2. Ввести обозначения для критериев, варьируемых при переменных задачи.
3. Выбрать критерий и определить его зависимость от варьируемых переменных.
4. Определить множество «D», т.е. составить все математические соотношения между варьируемыми переменными, определяющие возможность их выбора.
Оптимизационная задача классифицируется:




















Задачи определения max функции одной переменной
Постановка задачи: Для функции 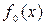 нужно определить max при условии
нужно определить max при условии 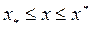
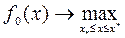 (1)
(1)
Множество «D», заданное (1) всегда выпуклое.
Определение: функция 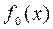 называется выпуклой на множестве «D», если она имеет на нем единственный max .
называется выпуклой на множестве «D», если она имеет на нем единственный max .
Для решения оптимизационных задач применяются методы, которые условно делятся на две группы:
1) аналитические, которые используют необходимое или достаточное условие максимума
2) численные методы
Необходимое условие, это условие при невыполнении которого событие невозможно, однако при его выполнении событие не обязательно имеет место.
Достаточным называется условие, выполнение которого гарантирует наступление события, однако его невыполнение не означает, что событие наступить не может.
Необходимое и достаточное условие максимума функции одной переменной
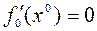 - необходимое условие
- необходимое условие
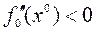 - достаточное условие
- достаточное условие
 Метод золотого сечения
Метод золотого сечения
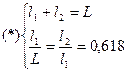
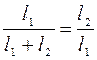 ;
; 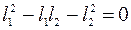 помножим на
помножим на 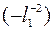
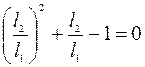 ;
; 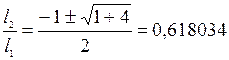
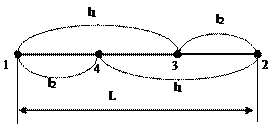
На каждом шаге расчета внутри интервала неопределенности определяют положение двух точек (№3 и №4), которое должно удовлетворять условиям (*). Вычисляют значение функции в этих точках, сравнивают их между собой и сокращают интервал неопределенности «L» до значения « 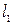 », так , чтобы внутри «
», так , чтобы внутри « 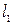 » сохранялась точка с наибольшим значением функции. Внутри сокращенного интервала неопределенности оставшаяся точка располагается в соответствии с соотношением (*). Поэтому на каждом шаге расчета, кроме первого, требуется вычислять значение целевой функции только один раз.
» сохранялась точка с наибольшим значением функции. Внутри сокращенного интервала неопределенности оставшаяся точка располагается в соответствии с соотношением (*). Поэтому на каждом шаге расчета, кроме первого, требуется вычислять значение целевой функции только один раз.
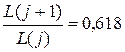 и
и
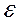 - погрешность (допустимая ошибка)
- погрешность (допустимая ошибка)
Расчет продолжается до тех пор, пока интервал неопределенности (L) не будет меньше погрешности 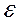 .
.
Необходимое и достаточное условие max функции многих переменных (безусловного)
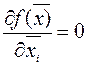
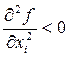
необходимое достаточное
Определение условного максимума
функции многих переменных
(задача нелинейного программирования)
Определить максимум функции функции 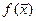 для
для 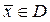 .
.
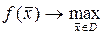 (1)
(1)
Где
|
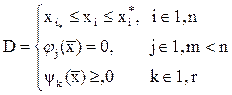
Метод неопределенных множителей Лагранжа
Рассматривается подзадача определения max, заданная только условиями (2) и (3)
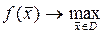
D: 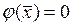 (5)
(5)
Составляем новую функцию.
L-функция Лагранжа
L 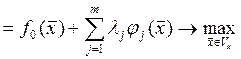
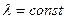 -неопределенный множитель Лагранжа
-неопределенный множитель Лагранжа
При выполнении уравнения связи (5) функция Лагранжа совпадает с функцией (1).
Если вычислить max функции Лагранжа при произвольной 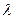 , то
, то 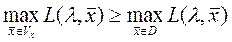 (6)
(6)
Из (6) следует, что: максимум функции Лагранжа по « 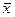 » при произвольной «
» при произвольной « 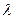 »
» 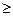 максимуму той же функции по «
максимуму той же функции по « 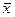 » при оптимальном «
» при оптимальном « 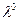 », т.е.в точке решения
», т.е.в точке решения  [
[ 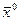 ,
, 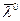 ] функция Лагранжа достигает max по «
] функция Лагранжа достигает max по « 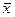 » и min по «
» и min по « 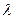 ». Это седловая точка функции Лагранжа.
». Это седловая точка функции Лагранжа.
Условия оптимальности:
L( 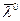 ,
, 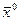 )=
)= 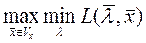 (7)
(7)
Теорема Куна-Такера – дает условие оптимальности для решения задачи условного максимума (1) ¸(4).
Функция Лагранжа общего вида:
L( 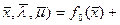
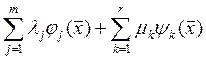 (8)
(8)
Если 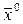 - решение задачи (1) ¸(4), то найдутся такие
- решение задачи (1) ¸(4), то найдутся такие 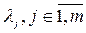 , и такие
, и такие 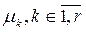 одновременно не равные нулю, что при
одновременно не равные нулю, что при 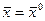 функция (8) достигает максимума по
функция (8) достигает максимума по 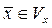 , минимума по
, минимума по 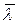 , а также все
, а также все 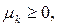 а
а 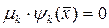 .
.
Условия оптимальности:
L( 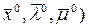 =
= 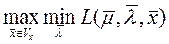
При условии
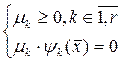
1) если 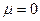 , то д.б.
, то д.б. 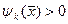
2) если 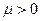 , то д.б.
, то д.б. 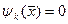
| <== предыдущая лекция | | | следующая лекция ==> |
| ПОСТРОЕНИЕ БАЗИСНОЙ СЕТКИ ЧЕРТЕЖА | | | Спирометрия и спирография |
Дата добавления: 2016-06-24; просмотров: 872;
