Пространственное распределение электрона в атоме водорода.

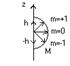Рассмотрим систему, состоящую из неподвижного ядра зарядом +z и 1-го электрона, находящегося около ядра (атом водорода или водородоподобная система). Потенциальная функция U(r)=-ze(c. 2)/4πε₀r(c.2). Стационарное уравнение Шредингера для этого случая имеет вид Dψ+ (2m/ħ(c.2))*(E+(1/4πε₀ )*(ze(c.2)/r(c.2))*ψ=0. Для решения этого уравнения удобно перейти к сферическим координатам: ψ(x,y,z)=ψ(r,θ,φ). Расчёты показывают, что это уравнение Шредингера имеет решение при любом E>0(электрон вне атома). И при E<0, удовлетворяющие условию: E_n=-(1/4πε₀)*(mz(c.2)e(c.4)/2ħ(c.2))*(1/n(с.2)). Решение уравнения Шредингера удобно искать в виде ψ(r,θ,φ)=R(r)θ(θ)Ф(φ), т.е. представим волновую функцию в виде произведения 3-х функций, каждая из кот-х зависит только от 1 переменной. R(r)-радиальная функция распределения; θ(θ) и Ф(φ) – функции углового распределения. В зависимости от значения орбитального квантового числа L=0,1,2,3,… состояние электрона в атоме обозначают s,p,d,f. Для электрона 1s-состоянии(n=1,L=0) функция радиального распределения R(r) имеет вид: Максимум этой функции приходится на r=0,529Å, т.е. совпадает с 1-м боровским радиусом. Функция углового распределения для 1s состояния: Для электронов p-состояний функция углового распределения имеет вид в зависимости от значения магнитного квантового числа: Видно, что современным представлениям соответствуют не орбиты, по кот-м движется электрон в атоме, а некоторая совокупность положений электронов в атоме(электронное облако, форма кот-го определяется значением квантовых чисел m, n, L, поэтому вместо термина орбита используют термин орбиталь. Каждой орбитали соответствует своё состояние электрона в вакууме, описанное волновой функцией. M_z=mħ p-состояние: L=1;m=0,±1

Видно, что положение вектора М в пространстве квантуется. Он может принимать только определённое положение в пространстве. Энергия электрона в атоме зависит от главного квантового числа n. Однако, при данном значении n, кроме n=1, значение L и m могут быть разными. Это значит, что одному и тому же уровню энергии E_n(собственное значение энергии) соответствует несколько различных состояний, каждое из которых описано своей волновой функцией. Состояния с одинаковыми энергиями наз-ся вырожденными. Число состояний, обладающих данным значением энергии E_n наз-ся кратностью вырождения. Кратность вырождения можно сосчитать по формуле: Σ[L=0, n-1] (2L+1)=2*n(c.2).