Граничные условия при однофазном КЗ с одновременным разрывом фазы в сети с глухозаземлённой нейтралью.

Ответ:Рассмотрим случай, когда одновременно возникают поперечная и продольная несимметрии. Пусть на каком-либо участке сети, нейтраль которой заземлена, произошел разрыв одного провода, причем один конец провода заземлился, а другой остался изолированным (рис. 8.6). Питание данного участка предполагается с обеих его сторон. Граничные условия при однофазном КЗ с разрывом фазы будут:

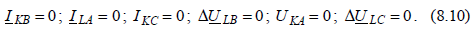
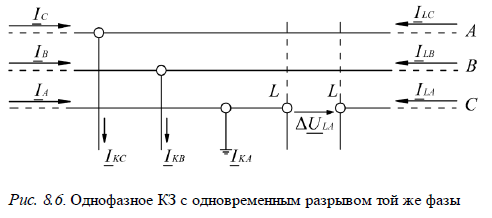Основные уравнения:

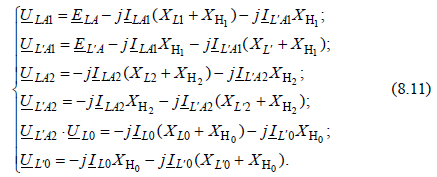Используя граничные условия (8.10) и основные уравнения (8.11), получим дополнительную связь между неизвестными токами и напряжениями прямой последовательности в местах несимметрии:

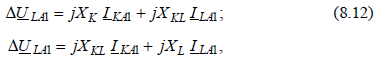где где 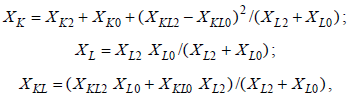ХK2, ХK0 – реактивности схемы соответствующей последовательности относительно точки КЗ при разрыве схемы в точке L; XL2, XL0 – то же относительно места разрыва при отсутствии КЗ; XKL2, XKL0 – взаимные реактивности между точкой КЗ и местом разрыва в схемах соответствующих последовательностей. Придадим уравнениям (8.12) несколько иной вид, введя в правую часть каждого уравнения два одинаковых, но противоположных по знаку, слагаемых:

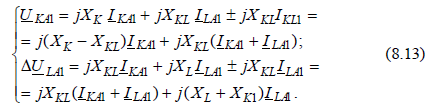Из уравнения (8.12) следует, что при рассматриваемой двухкратной несимметрии расчет токов и напряжений прямой последовательности (при ранее принятых допущениях) сводится к расчету эквивалентного КЗ в некоторой точке С, связанной с точками L1 и L1 схемы прямой последовательности реактивными сопротивлениями XKL, (XK – XKL) и (XL – XKL), величины которых определяются реактивными сопротивлениями только схем обратной и нулевой последовательностей. Таким образом, в данном случае соблюдается правило эквивалентности прямой последовательности со всеми вытекающими из него следствиями. Следует отметить, что при расчетах за положительное направление тока ILA1 принято направление от места замыкания. Чтобы увязать с обычно принимаемым условием, что токи имеют положительное направление к точке КЗ, необходимо у найденного тока ILA1 изменить знак. Напряжение прямой последовательности в месте КЗ относительно нулевого провода и относительно оборванного конца фазы (ΔULA1) определяются суммой соответствующих падений напряжений в схеме. Остальные симметричные составляющие токов и напряжений в

обоих местах несимметрии определяются из соотношений, которые вытекают из граничных условий и уравнений связи (8.2) и (8.3). Распределение токов и напряжений находят с использованием принципа наложения. Если приведенные ЭДС источников равны между собой, и параметры прямой и обратной последовательностей принять одинаковыми, то для определения тока прямой последовательности в месте КЗ при одновременном разрыве той же фазы с одной стороны можно получить расчетное выражение

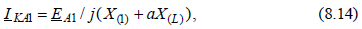где Х(1) = 2Х1 + Х0 – результирующая реактивность при однофазном КЗ в точке К и отсутствии разрыва фазы в точке L;

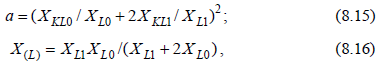где ХL1 и XKL1 – то же, что ранее XL2 и XKL2.