Сложные виды повреждений. Разновидности. Граничные условия при двойном замыкании на землю в сети с изолированной нейтралью.

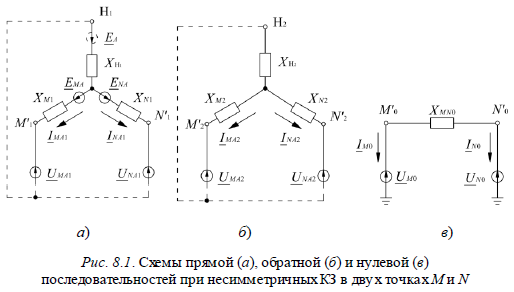
Ответ:Сложные виды повреждений представляют собой совокупность нескольких несимметричных замыканий или нарушений продольной несимметрии отдельных участков системы. Возможны случаи, когда в системе одновременно возникают как поперечные, так и продольные несимметрии в самых различных комбинациях. Практический интерес обычно представляет одновременное нарушение симметрии лишь в двух точках системы, так как более сложные повреждения являются редкими исключениями. Поэтому в дальнейшем рассмотрим лишь двухкратную несимметрию, причем будем предполагать, что обе несимметрии возникают одновременно. Рассмотрим основные принципы расчета таких повреждений. Их конкретное применение показано на двух наиболее часто встречающихся случаях: при двойных замыканиях на землю в сети с изолированной нейтралью и при однофазном КЗ с одновременным разрывом фазы. Любая несимметрия характеризуется симметричными составляющими токов и напряжений в месте несимметрии. Следовательно, при двухкратной несимметрии подлежат определению двенадцать неизвестных величин – по три симметричных составляющих напряжений и токов в каждой точке несимметрии. Для определения этих неизвестных нужно составить такое же число независимых уравнений. В гл. 6 и 7 было установлено, что из граничных условий возникшей несимметрии непосредственно вытекают три соотношения для симметричных составляющих напряжений и токов в месте несимметрии. Таким образом, при двухкратной несимметрии половина общего числа необходимых уравнений является следствием граничных условий. Остальные уравнения можно получить, рассматриваясвязи между токами и напряжениями одноименных последовательностей. Так, при поперечных несимметриях одновременно в произвольных точках M и N заданной системы, схемы отдельных последовательностей которой после преобразований могут быть представлены в виде эквивалентных трехлучевых звезд (рис. 8.1), из которых составим уравнения для составляющих напряжений в точках M и N:

- для прямой последовательности (рис. 8.1, а): 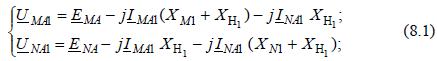- для обратной последовательности (рис. 8.1, б): 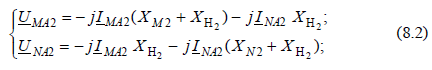- для нулевой последовательности (рис. 8.1, в):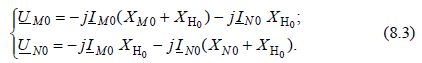 При анализе сложных видов повреждений правило эквивалентности прямой последовательности при несимметрии в одной точке распространяется на двухкратную несимметрию. Поэтому в такихслучаях могут быть использованы все практические методы расчета, которые используются при однократной несимметрии. Предположим в произвольных точках M и N сети, работающей с изолированной или резонансно заземленной нейтралью, произошли одновременные замыкания на землю фаз B и C (рис. 8.2). При этом для упрощения примем, что оба замыкания являются металлическими, а все элементы сети – чисто индуктивными. Граничные условия в точках замыкания будут:

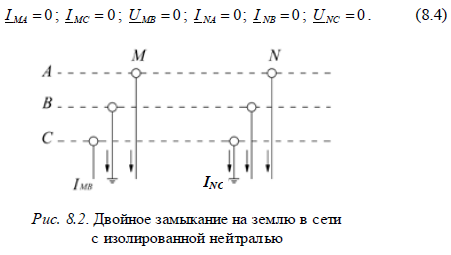Дополнительным условием является равенство Приняв неповрежденную фазу A за основную, запишем через симметричные составляющие следствия, которые вытекают из граничных условий (8.4) и анализа однофазного КЗ (гл. 6):

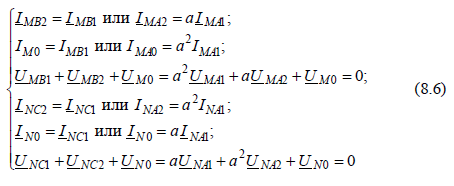и, учитывая граничные условия (8.4) в соответствии с (8.6), получим:

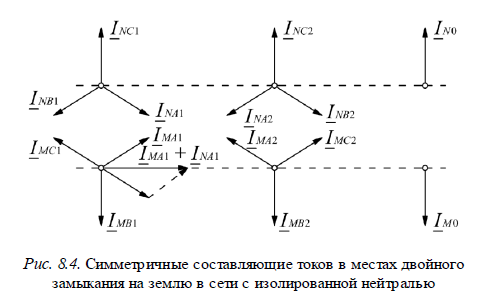
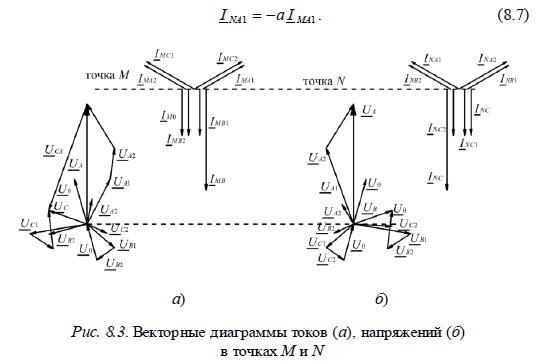Равенство (8.7) показывает, что симметричные составляющие токов в обоих местах замыкания не являются независимыми переменными, а находятся в жесткой связи между собой, как это иллюстрируют векторные диаграммы на рис. 8.4.

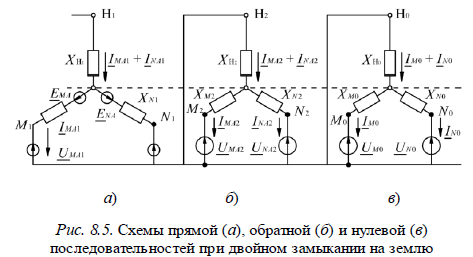
Схемы отдельных последовательностей для рассматриваемого случая приведены на рис. 8.5. Уравнения связи между токами и напряжениями прямой и обратной последовательностей в точках M и N (рис. 8.2) сохраняют тот же вид, что и уравнения (8.1)–(8.3).

Благодаря простоте соотношений, вытекающих из граничных условий, решение полученной системы уравнений (8.6) сводится к замене всех неизвестных. Для тока поврежденных фаз в местах замыкания на землю имеем: 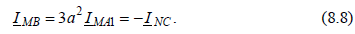Выражения для симметричных составляющих напряжений в точках M и N удобнее представить через ток 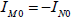и при этом получить:

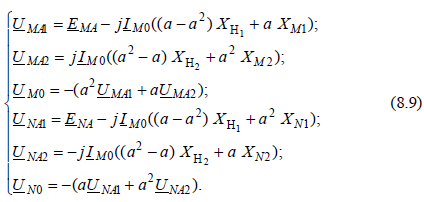На рис. 8.3, а, б приведены векторные диаграммы токов и напряжений в местах двойного замыкания на землю. Диаграммы напряжений показывают, что величины и сдвиги фазных напряжений зависят от соотношения между реактивными сопротивлениями схем отдельных последовательностей.