Радиальная базисная сеть

Под термином сеть радиально-базисных функция понимается любая нейронная сеть, которая содержит скрытый слой нейронов с радиально-симметричной функцией активации, каждый из которых предназначен для хранения отдельного эталонного вектора в виде вектора весов.

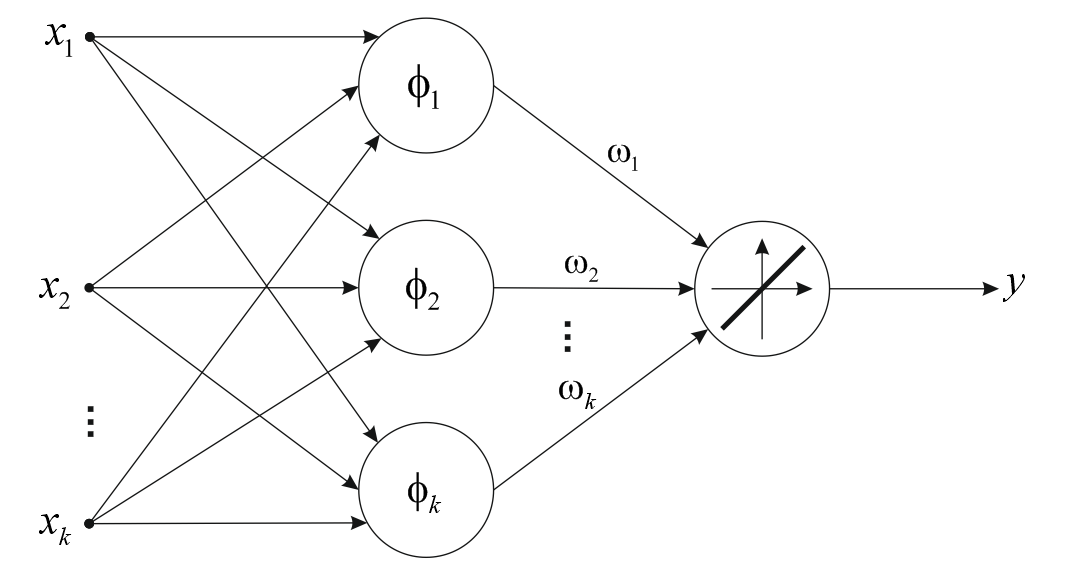
Рисунок 25 Радиальная базисная сеть

Сети с радиально-базисной функцией в скрытом слое содержит нейроны, которые реализуют функции радиально изменяющиеся вокруг выбранного центра и принадлежащие ненулевые значения только в окрестности этого центра. Подобные функции, определяемые как 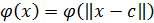, будем называть радиально-базисными функциями.

Структура типичной радиальной сети включает входной слой, на который подаются сигналы, описывающие входной вектор X, скрытый слой с нейронном радиального типа и выходной слой, состоящий из 1 или нескольких линейных нейронов. Функция выходного нейрона сводится к взвешиванию суммированных сигналов, генерируемых скрытыми нейронами.

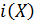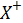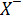Радиальные сети предназначены для решения задач классификации. Если вектор радиальной функции в n-мерном входном пространстве обозначить как , то это пространство является нелинейно разделяемым на два пространственных класса и только тогда, когда существует такой вектор весов 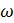, что:

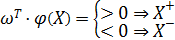
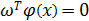- граница между классами 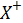и .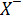

Применение достаточно большого количества скрытых нейронов, реализующих радиальные функции, гарантирует решение задачи классификации даже при построении всего лишь двухслойной сети.

Простейшая нейронная сеть радиального типа функционирует по принципу многомерной интерполяции, состоящей в отображении множества входных векторов на множество числе 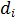. При очень большом количестве обучающих выборок и равном ему количестве радиальных функций сеть становится громоздкой, поэтому необходимо уменьшить количество радиальных функций и получить дополнительную информацию для структуризации задачи.

В качестве радиальной функции применяется функция Гаусса. При размещении её центра в 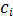она может быть определена как:

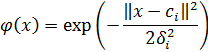
Аргументом радиальной функции является евклидово расстояние образца x от центра .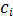

29.10.2011