Многофакторный дисперсионный анализ
Применяется при одновременном влиянии нескольких факторов.
- как уровень рекламы и уровень цен (высокий, средний, низкий) одновременно влияют на продажи товара данной торговой марки?
- влияет ли на выбор потребителем данной торговой марки уровень образования и возраст?
Многофакторный дисперсионный анализ позволяет изучать взаимодействие факторов.
Взаимодействие имеет место, когда эффекты одного фактора на зависимую переменную зависят от уровня других факторов.
Рассмотрим пример, в который входят факторы Х1 и Х2 с уровнями с1 и с2.
В этом случае полная вариация раскладывается следующим образом:
SSу = SSх1 + SSх2 + SSх1х2 + SSошибки
Если Х1 и Х2 не зависят друг от друга, то SSх1х2 приближается к нулю.
Эффект двух факторов называют множественной корреляцией
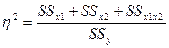
Значимость эффекта проверяется также как в случае однофакторного дисперсионного анализа – с помощью критерия Фишера.
Нулевая гипотеза
Н0: взаимодействие между факторами отсутствует.
Иллюстрация.
Изучим эффекты, обусловленные влиянием уровня внутримагазинной рекламы и уровня купонной распродажи на продажи магазина.
Результаты компьютерного анализа приведены в табл.4.
Табл.4. – Двухфакторный дисперсионный анализ
| Источник вариации Главные эффекты | Сумма квадратов | Степени свободы | Средний квадрат | F - статистика | Вероятность (значимость) F | 
|
| Внутримагазинная реклама | 106,067 | 53,033 | 54,862 | 0,000 | 0,557 | |
| 53,333 | 53,333 | 55,172 | 0,000 | 0,280 | ||
| Объединенный | 159,400 | 53,133 | 54,966 | 0,000 | ||
| Двухфакторное взаимодействие | 3,267 | 1,633 | 1,69 | 0,206 | ||
| Модель | 162,667 | 32,533 | 33,655 | 0,000 | ||
| Остаточный компонент (ошибка) | 23,200 | 0,967 | ||||
| Итого | 185,867 | 6,409 |
Средние ячеек
| Уровень внутримагазинной рекламы | Купонная распродажа | Количество наблюдений | Среднее |
| Высокий | Да | 9,2 | |
| Высокий | Нет | 7,4 | |
| Средний | Да | 7,6 | |
| Средний | Нет | 4,8 | |
| Низкий | Да | 5,4 | |
| Низкий | Нет | 2,0 |
Дата добавления: 2016-05-05; просмотров: 682;
