Дисперсионный анализ
11.1. Дисперсионный анализ – статистический метод изучения различий между выборочными средними для двух или более совокупностей.
Фактор – категориальная независимая переменная.
Часто у маркетологов возникает необходимость установить различия в средних значениях зависимой переменной для нескольких категорий одной независимой переменной фактора.
Например:
- Различаются ли сегменты рынка с точки зрения объема потребления товара?
Х
I сегмент II сегмент
У уровни потребления
- Различаются ли оценки торговой марки группами респондентов, которые посмотрели разные рекламные ролики?
Х
I ролик II ролик IIIролик
У оценки торговой марки
- Зависит ли намерение потребителей приобрести товар данной торговой марки от разницы в уровне цен?
Х
Низкая Средняя Высокая
У намерения потребителей
Выполнение однофакторного дисперсионного анализа состоит из следующих этапов:
1. Определение зависимой и независимой переменных;
2. Разложение полной дисперсии;
3. Измерение эффектов;
4. Проверка значимости;
5. Интерпретация результатов.
Этап 1. Пусть У – зависимая переменная (метрическая), а Х – независимая переменная, имеющая с категорий (уровней). Для каждой группы Х существует n наблюдений У. Размер общей выборки N=n×c.
Группы
Х1 Х2 . . . Хс
 |
У11 У12 . . . У1с
У21 У22 . . . У2с
. . . Внутригрупповая вариация
. . . SSошибки
Уn1 Уn2 . . . Уnс
Групповые средние 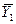
 . . .
. . . 
Межгрупповая вариация (SSх)
Этап 2.Разложение полной дисперсии в однофакторном дисперсионном анализе – это разделение вариации зависимой переменной на вариацию, обусловленную различием средних между группами, плюс вариацию, обусловленную внутригрупповой изменчивостью.
Полную вариацию SSу можно разложить на два компонента:
SSх (межгрупповая вариация – вариация между категориями переменной Х);
SSошибки (внутригрупповая вариация – вариация У внутри каждой группы Х)
SSу = SSх + SSошибки
где SSу = 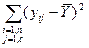
SSх = 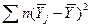
SSошибки = 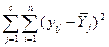
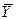 - среднее для всей выборки;
- среднее для всей выборки;
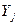 - среднее для группы j
- среднее для группы j
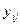 - i наблюдение в j группе.
- i наблюдение в j группе.
Этап 3. Измерение эффекта. Сила влияния переменной Х на У измеряется с помощью SSx. SSx растет с увеличением различий между средними значениями У в группах Х.
Эффект влияния переменной Х на У вычисляют по формуле:
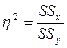 - корреляционное отношение
- корреляционное отношение
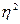 изменяется от 0 до 1. Оно равно 0, когда все групповые средние равны, т.е. Х не влияет на У.
изменяется от 0 до 1. Оно равно 0, когда все групповые средние равны, т.е. Х не влияет на У. 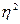 = 1, когда внутри каждой группы изменчивость отсутствует, но имеется некоторая изменчивость между группами.
= 1, когда внутри каждой группы изменчивость отсутствует, но имеется некоторая изменчивость между группами.
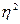 - мера вариации У, объясненная влиянием независимой переменной Х.
- мера вариации У, объясненная влиянием независимой переменной Х.
Этап 4.Проверка значимости. В однофакторном дисперсионном анализе проверяют нулевую гипотезу, утверждающую, что групповые средние равны:
Н0: 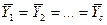 .
.
Нулевую гипотезу можно проверить с помощью F – статистики:
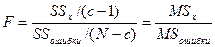
где MS – средний квадрат.
Эта статистики подчиняется F – распределению с числом степеней свободы (df), равным (с-1) и (N-c).
Этап 5. Интерпретация результатов. Если нулевую гипотезу о равенстве групповых средних не отклоняют, то независимая переменная не оказывает статистически значимого влияния на зависимую переменную.
Если нулевую гипотезу отклоняют, то эффект независимой переменой на зависимую трактуется, как статистически значимый. Другими словами, среднее значение зависимой переменной различно для различных групп независимой переменной.
Иллюстрация.
Цель эксперимента – изучать влияние уровня рекламы товаров непосредственно в самом магазине и купонной распродажи на объем продаж.
Маркетологи использовали три уровня рекламы товаров в магазине: 1 – высокий, 2 – средний, 3 – низкий. У купонной распродажи было 2 уровня: 1 – наличие 10 грн. купона, 2 – отсутствие.
Тридцать магазинов были выбраны случайным образом, и для каждой комбинации условий эксперимента случайным образом взяли по пять магазинов. Эксперимент продолжался два месяца. Определили объем продаж в каждом магазине, нормализовали его, приняв во внимание посторонние факторы (размер магазина, товарооборот и т.д.) и пересчитали по 10-бальной шкале. В дополнение была получена качественная оценка относительного числа постоянных покупателей магазина (по 10-бальной) шкале. (табл.1.)
Табл.1.– Уровень купонной распродажи, реклама товаров на месте купли-продажи, продажи и постоянные покупатели
| Номер магазина | Уровень купонной распродажи | Внутримагазинная реклама | Продажи | Постоянные покупатели |
Предположим, что рассматривается только один фактор – реклама на месте торговли. Исследуем влияние внутримагазинной рекламы (Х) на продажи (У) (табл.2).
Табл. 2.– Влияние уровня внутримагазинной рекламы на продажи
| Номер магазина | Уровень рекламы | ||
| Высокий | Средний | Низкий | |
| Суммы по столбцам | |||
Групповые средние: 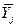
| 8,3 | 6,2 | 3,7 |
Общее среднее 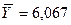
|
Тот же результат можно получить с помощью программы SPSS (рис.1, рис.2, рис.3). Для этого в меню Анализ выбираем подменю Таблицы, Базовые таблицы (рис.1). Зависимая переменная у нас – уровень продаж, независимая – уровень рекламы (рис.2). Результат – средние значения для каждой категории уровня рекламы (рис.3).
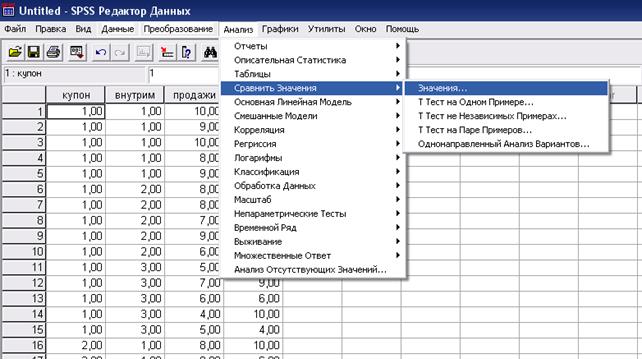
Рис.1. Выбор меню
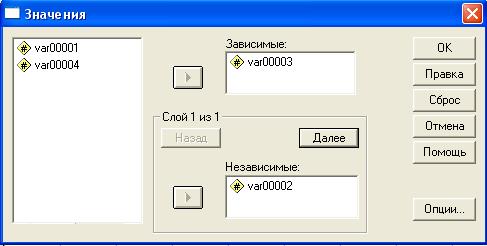
Рис.2. Выбор зависимых и независимых переменных
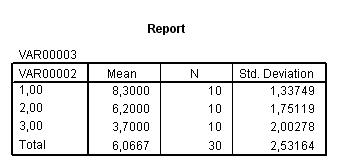
Рис.3. Результат Базовой таблицы.
Нулевая гипотеза для проведения однофакторного дисперсионного анализа формулируется следующим образом:
Н0: 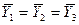 .
.
Вычислим общую вариацию
SSy = (10 – 6,067)2 + (9 – 6,067)2 + . . . + (2 – 6,067)2 = 185, 867 (от всех значений таблицы вычитается общее среднее У, полученная разность возводится в квадрат и затем суммируется.
Вычислим межгрупповую вариацию
SSх = 10(8,3 – 6,067)2 + 10(6,2 – 6,067)2 + 10(3,7 – 6,067)2 = 106,067
Вычислим внутригрупповую вариацию
SSошибки = (10-8,3)2 + (9 – 8,3)2 + . . . + (6 – 8,3)2 +
+ (8 – 6,2)2 + (8 – 6,2)2 + . . . + (4 – 6,2)2 +
+ (5 – 3,7)2 + (7 – 3,7)2 + . . . + (2 – 3,7)2 = 79,80
Можно проверить, что
SSу = SSх + SSошибки
185,867 = 106,067 + 79,80
эффект
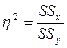 = 0,571
= 0,571
57,1% вариации в продажах (У) обусловлено влиянием внутримагазинной рекламы (Х) – это умеренный эффект.
Проверим нулевую гипотезу
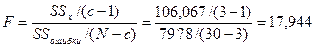
Из статистических таблиц находим для 2 и 27 степеней свободы критическое значение Fкр = 3,35 при уровне значимости 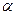 = 0,05. Поскольку F > Fкр, то нулевую гипотезу отклоняют. Средние значения генеральных совокупностей для трех уровней внутримагазинной рекламы различаются между собой.
= 0,05. Поскольку F > Fкр, то нулевую гипотезу отклоняют. Средние значения генеральных совокупностей для трех уровней внутримагазинной рекламы различаются между собой.
Компьютерный результат представлен в таблице 3 и на рис.4, рис.5, рис.6.
Табл. 3. – Однофакторный дисперсионный анализ (ANOVA)
| Источник дисперсии | Сумма квадратов | Степени свободы | Средний квадрат | F - статистика | Вероятность F |
| Между группами (внутримагазинная реклама) | 106,067 | 53,033 | 17,944 | 0,000 | |
| Внутри групп (дисперсия ошибки) | 79,800 | 2,956 | |||
| Итого | 185,867 | 6,409 |
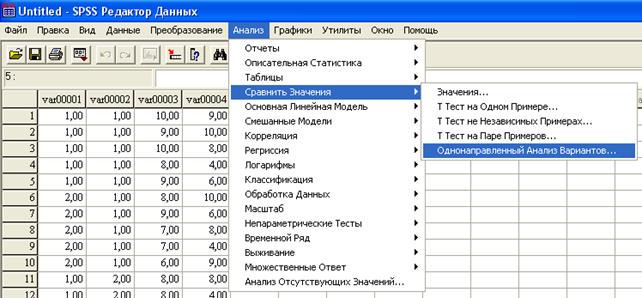
Рис.4. Выбор метода однофакторного дисперсионного анализа
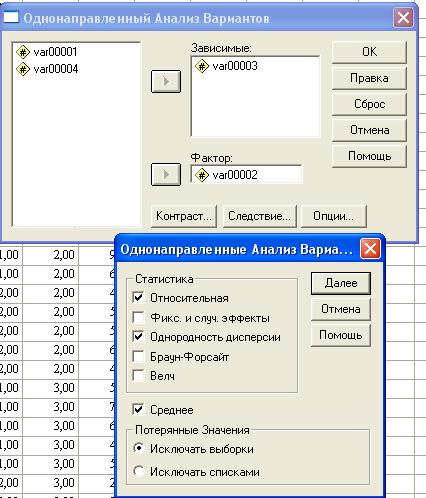
Рис.5. Выбор зависимой переменной и фактора (независимой переменной)
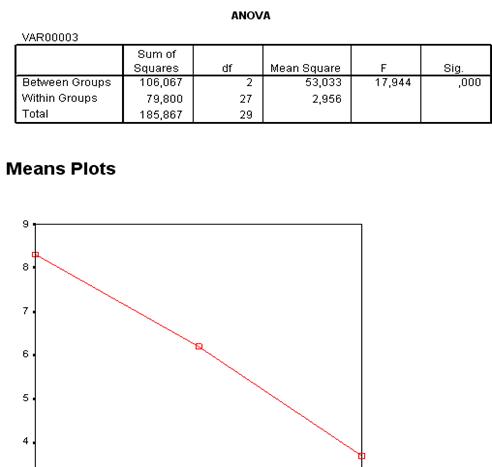
Рис.6. Результат дисперсионного анализа.
Дата добавления: 2016-05-05; просмотров: 1321;
