Таблицы на деревьях

Рассмотрим еще один способ организации таблиц символов с использованием двоичных деревьев.

Ориентированное дерево называется двоичным, если у него в каждую вершину, кроме одной ( корня ), входит одна дуга, и из каждой вершины выходит не более двух дуг. Ветвью дерева называется поддерево, состоящее из некоторой дуги данного дерева, ее начальной и конечной вершин, а также всех вершин и дуг, лежащих на всех путях, выходящих из конечной вершины этой дуги.Высотой дерева называется максимальная длина пути в этом дереве от корня до листа.

Пусть на множестве идентификаторов задан некоторый линейный (например, лексикографический) порядок 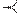, то есть некоторое транзитивное, антисимметричное и антирефлексивное отношение. Таким образом, для произвольной пары идентификаторов id₁ иid₂ либо 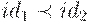, либо 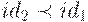, либо id₁ совпадает с id₂.

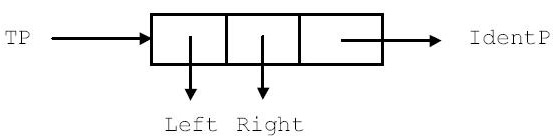
Рис. 7.5.

Каждой вершине двоичного дерева, представляющего таблицу символов, сопоставим идентификатор. При этом, если вершина (которой сопоставлен id ) имеет левого потомка (которому сопоставлен id_L ), то 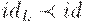; если имеет правого потомка(id_R), то . Элемент таблицы изображен на рис. 7.5.

Поиск в такой таблице может быть описан следующей функцией:

где структура для для элемента дерева имеет вид

Занесение в таблицу осуществляется функцией

Как показано в работе [10], среднее время поиска в таблице размера n, организованной в виде двоичного дерева, при равной вероятности появления каждого объекта равно (2 ln 2) log₂n + O(1). Однако, на практике случай равной вероятности появления объектов встречается довольно редко. Поэтому в дереве появляются более длинные и более короткие ветви, и среднее время поиска увеличивается.

Чтобы уменьшить среднее время поиска в двоичном дереве, можно в процессе построения дерева следить за тем, чтобы оно все время оставалось сбалансированным. А именно, назовем дерево сбалансированным, если ни для какой вершины высота выходящей из нее правой ветви не отличается от высоты левой более чем на 1. Для того, чтобы достичь сбалансированности, в процессе добавления новых вершин дерево можно слегка перестраивать следующим образом [1].

Определим для каждой вершины дерева характеристику, равную разности высот выходящих из нее правой и левой ветвей. В сбалансированном дереве характеристика вершины может быть равной -1, 0 и 1, для листьев она равна 0.

Пусть мы определили место новой вершины в дереве. Ее характеристика равна 0. Назовем путь, ведущий от корня к новой вершине, выделенным. При добавлении новой вершины могут измениться характеристики только тех вершин, которые лежат на выделенном пути. Рассмотрим заключительный отрезок выделенного пути, такой, что до добавления вершины характеристики всех вершин на нем были равны 0. Если верхним концом этого отрезка является сам корень, то дерево перестраивать не надо, достаточно лишь изменить характеристики вершин на этом пути на 1 или -1, в зависимости от того, влево или вправо пристроена новая вершина.

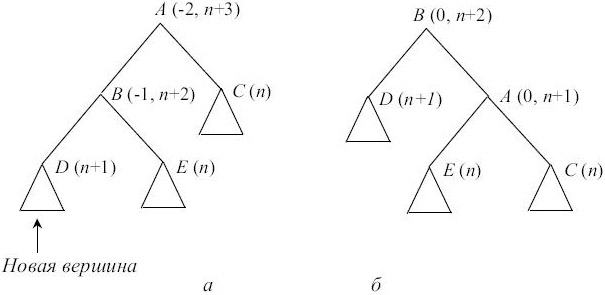
Рис. 7.6.

Рис. 7.7.

Пусть верхний конец заключительного отрезка - не корень. Рассмотрим вершину A - "родителя" верхнего конца заключительного отрезка. Перед добавлением новой вершины характеристика A была равна . Если A имела характеристику 1 (-1) и новая вершина добавляется в левую (правую) ветвь, то характеристика вершины A становится равной 0, а высота поддерева с корнем вA не меняется. Так что и в этом случае дерево перестраивать не надо. Пусть теперь характеристика A до перестраивания была равна -1 и новая вершина добавлена к левой ветви A (аналогично - для случая 1 и добавления к правой ветви). Рассмотрим вершину B - левого потомка A. Возможны следующие варианты.

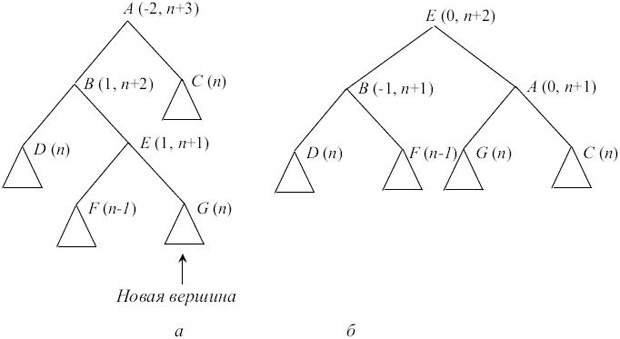
Рис. 7.8.

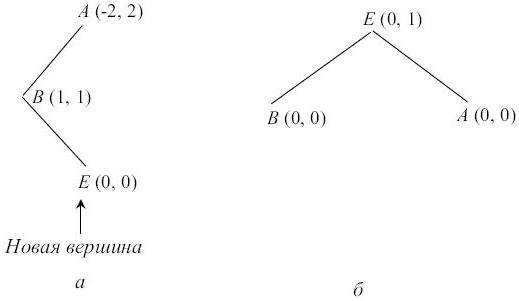
Рис. 7.9.

Если характеристика B после добавления новой вершины в D стала равна -1, то дерево имеет структуру, изображенную на рис. 7.6, а. Перестроив дерево так, как это изображено на рис. 7.6, б, мы добьемся сбалансированности (в скобках указаны характеристики вершин, где это существенно, и соотношения высот после добавления).

Если характеристика вершины B после добавления новой вершины в E стала равна 1, то надо отдельно рассмотреть случаи, когда характеристика вершины E, следующей за B на выделенном пути, стала равна -1, 1 и 0 (в последнем случае вершина E- новая). Вид дерева до и после перестройки для этих случаев показан соответственно на рис. 7.7, рис. 7.8 и рис. 7.9.