Графический способ изображения статистических данных.

Графическим способом изображения статистических данных называют их условное изображение при помощи точек, линий, плоскостей, геометрических фигур и условных знаков. Графики в статистике применяются для: сравнения одноименных показателей, относящихся к различным объектам; наглядного представления структуры совокупности и ее изменения; характеристики динамики и степени распространения явления; отображения взаимосвязи явлений.

В зависимости от назначения используют различные виды графиков: линейные, столбиковые, ленточные, секторные, фигурные.

Линейные диаграммыобычно применяют для характеристики динамики явлений, их взаимосвязи.

Столбиковые, ленточные диаграммыиспользуются для сравнения значений статистических показателей, характеризующих изучаемые объекты в разные моменты времени (за разные периоды времени).

Секторные диаграммыиспользуются для характеристики структуры совокупности.

Фигурные диаграммы используют при сравнении различных явлений по степени их распространения.

Дискретные вариационные ряды изображают в виде полигона (многоугольника) распределения.

Полигон распределения строится в прямоугольной системе координат. На оси абсцисс откладываются варианты, а на оси ординат наносится шкала частот. На оси абсцисс отмечаются точки, соответствующие величинам вариант, и из них восстанавливаются перпендикуляры, длины которых соответствуют частотам конкретных вариант. В результате соединения концов перпендикуляров отрезками прямой, получают полигон распределения. При этом первую точку следует соединить с точкой на оси абсцисс, соответствующей предшествующей варианте, частота которой равна нулю. Последнюю точку следует также соединить с точкой на оси абсцисс, соответствующей варианте, следующей за последней (частота ее также равна нулю). Таким образом получается многоугольник, изображающий распределение признака (рис. 1.1).

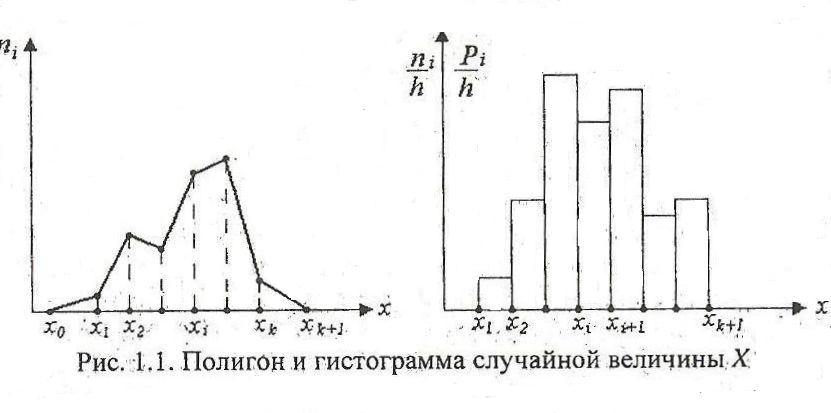
Интервальный ряд графически изображается в виде гистограммы (клеточного графика) распределения.

Гистограмма распределения - ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению n_i/h (плотность частоты). В этом случае частота обезличивается и в каждом интервале ее можно отнести к любому значению признака. Площадь i - го прямоугольника равна n_i, а площадь гистограммы равна объему выборки п.

Если частоты отнести к серединам интервалов и соединить ординаты прямыми, то получится полигон распределения.

Огива - графическое изображение рядов распределений по накопленным частотам.

В этом случае по оси абсцисс откладывают накопленные частоты (или частости), по оси ординат - значение признака по возрастающей величине. Соединяя точки, получают огиву распределения.

Корреляционная таблица - таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному. Концентрация частот около диагонали (любой) таблицы свидетельствует о наличии связи между признаками.