Методи розв’язування ДРЧП
Розрізняють десять груп методів розв’язування ДРЧП:
1. Методи розділення змінних: у випадку повного розділення змінних, ДРЧП з 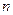 незалежними змінними зводиться до
незалежними змінними зводиться до 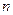 звичайних диференціальних рівнянь. При частковому розділенні змінних одне ДРЧП зводиться до декількох диференціального рівняння в частинних похідних з меншим числом незалежних змінних [5].
звичайних диференціальних рівнянь. При частковому розділенні змінних одне ДРЧП зводиться до декількох диференціального рівняння в частинних похідних з меншим числом незалежних змінних [5].
2. Методи інтегральних перетворень: дає змогу звести ДРЧП з 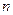 незалежними змінними до ДРЧП з (
незалежними змінними до ДРЧП з ( 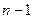 ) незалежними змінними, тобто зменшити кількість незалежних змінних.
) незалежними змінними, тобто зменшити кількість незалежних змінних.
3. Методи розв’язування координат: шляхом певного перетворення координат ДРЧП зводиться або до звичайного диференціального рівняння, або до більш простого диференціального рівняння в частинних похідних.
4. Перетворення залежної змінної: вихідне ДРЧП перетворюється до такого ДРЧП від іншої невідомої функції, яке розв’язується легше.
5. Чисельні методи: полягають у заміні диференціальних рівнянь їх дискретними різницевими аналогами або апроксимації шуканої функції інтерполяційними поліномами. У результаті розв’язування ДРЧП зводиться до розв’язування системи лінійних алгебраїчних рівнянь. Найбільш поширеними чисельними методами є: метод скінчених різниць, метод скінчених елементів та метод граничних елементів [5 - 16].
6. Методи теорії збурень: полягають у лінеаризації нелінійних рівнянь. Вихідна нелінійна задача зводиться до послідовності лінійних.
7. Методи функцій Гріна[16, 23]: початкові та граничні умови заміняються системою елементарних джерел (функцій Гріна) і задача розв’язується для кожного випадку. Повний розв’язок вихідної задачі отримують шляхом сумування розв’язків, отриманих для елементарних джерел.
8. Методи інтегральних рівнянь: диференціальне рівняння в частинних похідних зводиться до інтегрального рівняння, тобто рівняння, в якому невідома функція знаходиться під знаком інтегралу.
9. Варіаційні методи[22]: замість ДРЧП розв’язується деяка задача мінімізації функціоналу. Виявляється, що функція, яка є мінімумом деякого функціоналу, є також і розв’язком вихідного диференціального рівняння в частинних похідних. Варіаційні методи можна застосовувати лише тоді, коли існує відповідний функціонал, який в таких випадках є математичним записом фундаментальних законів природи, таких як закон збереження енергії.
10. Методи розкладу за власними функціями: розв’язок ДРЧП шукається у вигляді ряду за власними функціями. Ці власні функції є розв’язком так званої задачі на власні значення, що відповідає вихідній задачі для диференціального рівняння в частинних похідних.
Дата добавления: 2016-05-05; просмотров: 768;
