Динамика отказов при коррозинно-усталостном хлоридо-кислородном растрескивании

Коррозионная усталость сплавов при водородном охрупчивании

В частности, для КУ при лидирующем процессе усталости (2.15) преобразуется к виду

МП (t^lim) =1-d = S N_j(t_i + t^rlt )/ N_j^o [1- С_H (t_i + t^rlt )/ С_H^lim]( 2.16)

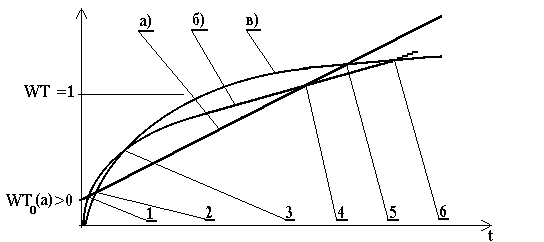
Рис. 8. Накопление меры повреждения по частным повреждающим процессам

где -С_Hи С_H^lim соответственно уравнение накопления водорода в конструкционном сплаве и предельное значение водорода в нем перед разрушением [21].

Если лидирует мера повреждения по наводороживанию, то (2.16) примет вид (2.17)

1-d = С_H (t_i + t^rlt )/ С_H^lim[1-S N_j(t_i + t ^rlt )/ N_j^o] (2.17)

Элементарными вычислениями можно подтвердить необходимость использования именно той или иной формулы в соответствии с вышеупомянутыми постулатами.

Детерминированное уравнение кинетики накопления усталостной меры повреждения дано в [18]

МП _z(t_i) = S N_jj / N_j^o + [(S N_ji / N_j^o - S N_jj^b / N_j^o)/ t_i] t^pr (2.18)

где - надстрочный индекс bотносит число циклов нагружения к пускона-ладочному периоду;

-t^pr - экспозиция упреждения – время работы после наработки t_i,после которого требуется знать усталостную меру повреждения.

Водород играет важную роль в долговечности конструкционных сплавов, однако его воздействие еще недавно не могло быть учтено так, как не был разработан математический аппарат накопления водорода гальванического происхождения в металле [22]

Детерминированное уравнение кинетики наводороживания сталей перлитного класса при кипении воды и имеет вид уравнений (1.13) – (1.14)

С_H(t_i) = k ( t_hi +Dt _i ) ^0,5 exp (-q pH_i) (2.19)

Подстановка в (2.16) или в (2.17) феноменологических уравнений (2.18), (2.19) и (1.14) позволит вычислить итерационным методом остаточный прогнозируемый остаточный ресурс t^rlt для случая коррозионной усталости с наводороживанием металла

1-d = С_H (t_i + t ^rlt )/ С_H^lim[1- SN_jj /N_j^o+[(SN_ji/N_j^o - S N_jj^b / N_j^o)/ t_i] t^rlt

(2.20)

Если в результате вычислений окажется, что прогнозируемый технический ресурс t^tech окажется меньше, чем назначенный ресурс t ^res

t^tech = t_i + t^rlt < t ^res, (2.21)

то целенаправленым изменением числовых значений фактор-аргументов техничейфскими средствами можно обеспечить продление ресурса.

Динамика отказов при коррозинно-усталостном хлоридо-кислородном растрескивании

Рис. 9 иллюстрирует динамику роста числа поврежденных трубок.

Критерий предельного состояния трубного пучка ПГВ (по физическому признаку) – это исчерпание технологического запаса трубок парогененратора с водой под давлением.

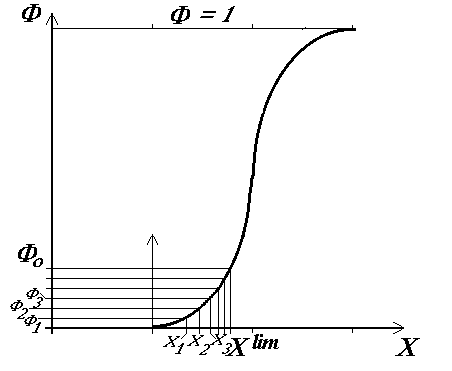Рис. 10. Динамика отказов теплообменных трубок парогенератора типа ПГВ

Т.е. предельное состояние трубного пучка наступает при достижении аргументом Х значенияX^lim. Если по значению Ф^lim , соответствующее технологическому запасу трубок P^lim, найти (по таблицам интеграла вероятности) соответствующееX^lim, то можно определить:

- предельное значение суммы Э ^lim в (2.23)

Э ^lim =[ SDt_i(C_Cl)_i^1,56] ^lim = ( X^lim - a) / b(2.24)

-где - Ф, Ф₀ = Ф^lim – соответвтвенно, текущее относительное значение числа заглушенных трубок по причине сквозного дефекта, и относительное значение технологического запаса трубок;

- Х_k, X^lim –текущее и предельное значения аргумента интеграла вероятности.

- SP_k, P^lim - текущее суммарное число поврежденных теплообменных трубок и полное число трубок в парогенераторе, соответственно.

- k –порядковый номер останова блока для поиска и герметизации теплообменных трубок со сквозными повреждениями.

- наработку до отказа трубного пучка при заданной на остаточный период эксплуатации хлорид-ионов (C_Cl) ^ост

t ^ост = {[ (X ^im – a)/ b] - SDt_i(C_Cl)_i^1,56 } / (C_Cl ^ост)^1,56 (2.25)

где – t ^ост – остаточный период эксплуатации трубного пучка ПГВ.

Этот прогноз можно сделать и через относительный аргументЭ/ Э^lim, после решения новой системы уравнений типа (9) и заменив a и bв ней,соответственно, на gи e.

t ^ост = {[(X ^im – g)/e] – (Э / Э ^lim) (2.26)

где- Э –текущее значение переменной части аргумента в (9) на дату прогнозных расчетов,

Э = SDt_i(C_Cl)_i^1,56 (2.27)

1.2.12. Прогнозирование технического ресурса трубного пучка парогенератора

Представляется закономерным, чтобы аргумент уравнения динамики отказов однотип-ных элементов в идентичных условиях содержал общая мера повреждения МП – функцию частных мер повреждения. В частности, мера повреждения по усталостиМП_Z, мера повреждения по хлоридо-кислородному растрескиванию WT_Cl и мера повреждения по образованию питтинговМП _Cu, соответственно.

Если вклад от какой-либо частной меры повреждения в общую меру повреждения не превышает погрешности метода расчета МП, то этим процессом можно пренебречь. При прогнозировании и обосновании новых характеристик остальные действия повторяются аналогично вычислениям согласно (2.24)-(2.25).

В таком случае, если предположить, чтоМП _Cl > МП > МП _Z, то уравнение (2.15) примет вид

X^lim- d₀ = g +

e {Э+t ^ост [К_Cl (C_Cl^rlt) ^{1, 56} } / Э^lim

+

{1-(M_Cu/M_Cu^lim)^2/3[t_н –t^о_Cu+t ^rlt) /(t_н –t^о_Cu)]^2/3/[1-SN_ij/Nj^im+(SN_ij/N_j^im -SN^b_ij/N_j^im)t ^rlt/t_н}

(2.31)

где - d₀ – погрешность методики прогноза остаточного ресурса трубного пучка при воздействии на него одновременно нескольких повреждающих процессов: усталости, хлоридо-кислородного растрескивания и питтингообразования.

Решая методом итераций (2.31) относительно t^rlt , получим время безопасной эксплуатации металла стенки теплообменной трубки парогенератора из аустенитной хромоникелевой стали марки 0Х18Н10Т.

Если соотношение МП_Cl, МП_Cuи МП_Z будет отличаться от принятого при выводе (2.31), в числителе дроби уравнения (2.31) будет стоять процесс с наибольшим числовым значением, а в знаменателе первой будет мера повреждения со следующим после числителя значением в порядке убывания. Замыкать знаменатель в (2.31) будет мера повреждения, характеризующая процесс с наименьшим числовым значением.

Варьированием переменных в (2.31), в частности:C_Cl^ост, скоростью образования отложений меди, скоростью накопления усталостного износа и другими, можно увеличить прогнозируемый ресурс.

1.2.13. Долговечность при радиационном охрупчивании

и коррозионной усталости металла

Известно, что наводороживание углеродистых сталей сдвигает в положительную область температуру хрупко-вязкого перехода. Усталость также приводит к подобному эффекту. Однако масштабы сдвига в настоящее время недостаточно обоснованно считаются пренебрежимо малыми. Это связано как с объективными научно-техническими трудностями, так и с преодолением субъективных, исторически сложившихся подходов и путей решения этой задачи.

Выражение (2.15) для расчета общей меры повреждения металла может быть адаптировано на случай неплакированного корпуса ядерного реактора. Если предположить, что числовые значения мер повреждения соотносятся между собойМП_ra > МП_H > МП_Z, то выражение (2.15) с использованием (1.7), ( (2.3), (2.4) 2.7) и (2.8) можно преобразовать для расчета остаточного срока безопасной эксплуатации, решая итерационным методом относительно t^rlt

___ ____

1- d = A_f [k S F ^rlt (t_hr + t ^rlt)]^{1/ 3} / T_k^o[ [1- k (t_hH + t ^rlt)^0,5 exp(- q pH ^rlt)] /

/C_H^lim × [1- (S N_j(t) - S N_j^b) (1 - t ^rlt / t) / N_j^o] ](2.32)

где - d – погрешность методики расчета;

- F^rlt – среднее значение мгновенного потока нейтронов на остаточный период эксплуатации;

- pH ^rlt

- T_k, T_k^lim – текущие значения температуры хрупко-вязкого перехода и, соответственно ее предельное значение;

- A_f , T_k^o – константы, определяющиеся состоянием и составом металла;

- k – константа, k = 10 ^-18 см² с/нейтрон;