Принцип работы долота. Дробящая способность шарошек

Принцип работы элементов вооружения дробяще-скалывающего долота показан на рис. 6.2 в. Качение шарошек по забою обеспечивается установкой их на цапфах с возможностью вращения, трением элементов вооружения о забой и сопротивлением горной породы скалыванию внедрившимися в нее элементами вооружения.

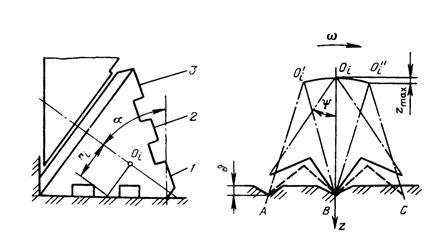
При перекатывании шарошки с одного элемента вооружения на другой создается дробящий эффект, а при проскальзывании вооружения относительно плоскости забоя создается скалывающий эффект.

Обеспечение и регулирование дробящей способности долота рассмотрим в соответствии со схемой на рис. 6.2. При перекатывании шарошек с зуба на зуб происходит вертикальное перемещение корпуса долота и связанного с ним бурильного инструмента. Потенциальная энергия перемещающегося и сжатого в вертикальном направлении низа бурильного инструмента является источником динамического воздействия долота на забой скважины. Теоретическое решение задачи о динамике работы долота возможно только с большими допущениями и дает лишь качественную картину. А поэтому для практических целей используются прямые измерения.

Принимаем, что названная потенциальная энергия инструмента U_и прямо пропорциональна вертикальному перемещению долота z:

U_и = А_иz, (6.1)

где А_и – коэффициент пропорциональности; z – вертикальное перемещение долота.

Для определения величины z рассмотрена условная шарошка с зубьями в венцах, выполненными на одной образующей конуса шарошки. Поскольку долото жесткое, то вертикальные перемещения точки О_i, лежащей на оси шарошки (цапфы) и долота совпадут. При опирании на два зуба в точках А и В ось шарошки находится в нижнем крайнем положении О_i^¢. По мере перекатывания шарошки зуб в точке В принимает вертикальное положение О_i. Тогда вертикальное перемещение оси шарошки, а вместе с ней и долота

z_max= z_Оi - z_Оi¢ = r_i sina(1 - cos(y/2)), (6.2)

где r_i – радиус венца; a - угол наклона оси шарошки к оси долота; y - угловой шаг зубьев в венце.

Из формулы (6.2) видно, что вертикальное перемещение долота растет с увеличением радиуса венца и его углового шага.

Для упрощения считаем, что горная порода деформируется на глубину d по линейному закону. Тогда баланс энергий

(6.3)

где U_П – потенциальная энергия деформирования горной породы, но

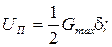(6.4)

G_ст. – статическая нагрузка на долото, задаваемая весом бурильного инструмента;

G_max – максимальная осевая нагрузка на долото.

Подставив в уравнение (6.3) значения U_и из выражения (6.1) и U_П из выражения (6.4) и сделав необходимые преобразования, получим

(6.5)

Обозначим величину 2А_иz /d = G_д и назовем ее динамической нагрузкой на долото, а отношение

G_max /G_ст = k_д (6.6)

коэффициентом динамичности.

Из формулы (6.5) видно, что динамическая нагрузка прямо пропорциональна вертикальному перемещению долота и обратно пропорциональна глубине деформирования горной породы.

При размещении зубьев всех венцов на одной образующей шарошки вертикальные перемещения корпуса долота будут обусловлены параметрами периферийных венцов. Например, для долот типа Т диаметром 190,5 мм величина z составила бы 0,92 мм, а динамическая нагрузка была бы чрезмерно большой и опасной как для долота, так и для бурильного инструмента. Поэтому в современных долотах зубья венцов размещают «вразбежку» так, чтобы зубья внутренних венцов были в свету зубьев периферийных венцов.