Глава 2. Описание характерных неопределенностей
И сравнительный анализ технологических
Процессов
2.1. Вероятностное описание неопределенностей
технологических процессов.
Характерные неопределенности, встречающиеся в описании состояний ТП как помехи, условно можно разделить на два класса: вероятностные и нечеткие.
Вероятностные помехи различных значений динамических переменных ТП описываются статистически обоснованными законами распределений вероятности их наступления, или первыми моментами – математическими ожиданиями, дисперсиями.
Нечеткие помехи различных значений динамических переменных ТП задаются лишь диапазонами их значений и некоторыми гипотетическими степенями принадлежности значений этим диапазонам.
Случайные события и их вероятности.
При испытании (наблюдении, опыте) каждому случайному событию, возможному в данном испытании, приписывают числовые меры его правдоподобия – частость и вероятность.
Пусть, например какая-то динамическая переменная S ТП(например, расход сырья)имеет некоторое частотное распределение wk своих «k»-ых разрядных значений (исходов) при максимальном значении исходов K, как показано на рис. 2.1.1.
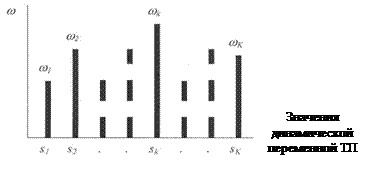 |
Рис. 2.1.1
Естественно, что для построения частот распределений, показанных на рисунке 2.1.1, первоначально необходимо иметь ряд эмпирических данных различных (и не всегда упорядоченных) значений {Sk} исследуемой переменной.
Каждому частотному распределению wk по теореме Бернулли может быть поставлена в соответствие эмпирическая или выборочная вероятность или частость wk/wå события «sk», где wå – общее число испытаний (объем выборки). Очевидно, что åKk wk = wå .
При wå ® ¥ выборочная вероятность будет стремиться к теоретической вероятности Prk (сокращенное от Probability). Однако на практике уже при wå @ 300 можно считать, что
Prk @ wk /wå = wk/åKk wk . (2.1.1)
Таким образом, под вероятностью PrA события A понимают отношение числа kA случаев, когда это событие наступило при испытании (динамическая переменная S ТП приняла значение A, т.е. S = A), к общему числу K всевозможных случаев в испытании
PrA = kA / K . (2.1.2)
Отсюда видно, что для любого события 0 £ Pr(A) £ 1, где вероятность невозможного события (которое никогда не происходит) принимается равной 0, а вероятность достоверного события (которое происходит всегда) принимается равной 1.
Функции распределений вероятностей
непрерывных случайных величин.
Рассмотренные выше вероятностные описания ТП были в основном связаны с дискретными случайными величинами, характеризовавшими как их динамические переменные, так и параметры структурного описания. Любая величина называется дискретной случайной величиной, если множество ее возможных значений конечно или счетно и принятие ею каждого из указанных значений есть случайное событие с определенной вероятностью.
Для вероятностного описания состояний ТП зачастую используют непрерывные случайные величины, характеризующие их динамические переменные, и функции их распределения.
Функцией F(s) распределения вероятностей случайной величины S называется вероятность того, что она примет значение, не превосходящее число s
F(s) = Pr(S £ s). (2.1.3)
Если функция распределения F(s) непрерывна и дифференцируема, то ее производная ¶F(s)/ ¶s называется плотностью распределения вероятностей p(s). Тогда функцию распределения вероятности можно определить как
F(s) = Pr(S £ s) = 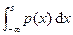 . (2.1.4)
. (2.1.4)
Из определения функции F(s), что она не убывает с ростом своего аргумента s.
В принципе, по аналогии с (2.1.4) можно ввести функцию распределения вероятностей и для дискретной случайной величины
F(s) = Pr(S £ s) = 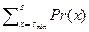 . (2.1.5)
. (2.1.5)
Заметим, что у дискретной случайной величины функция распределения ступенчатая, т.к. отражает сумму накопленных вероятностей Pr(x) случайных величин. Значение функции F(s) изменяется скачком при переходе с одного дискретного значения s на другое, как показано на рис. 2.1.2.
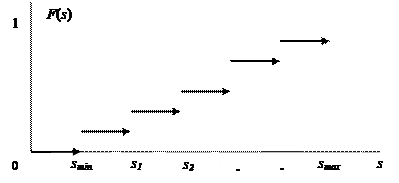 |
Рис. 2.1.2
Нормальная плотность распределения вероятностей.
В силу того обстоятельства, что любая помеха H, сопутствующая какой либо динамической переменной или параметру структурного описания ТП, зависит от огромного числа возмущающих факторов, справедлива гипотеза о ее нормальном распределении, опирающаяся на центральную предельную теорему.
Как известно, центральная предельная теорема гласит, что распределение суммарного (аддитивного) значения бесконечно большого числа независимых случайных величин описывается нормальным законом Гаусса (независимо от законов распределений этих величин). В условиях выдвинутой гипотезы, плотность распределения вероятностей p(H) или отклонений H = S – áSñ «N»-компонентного вектора состояния S от центрального (наиболее вероятного) вектора состояния áSñ ТП определяется многомерным нормальным законом распределения
pнор(H) = pнор(S) =
= exp[– (S – áSñ)+ COV-1(S – áSñ)]/(2p)N/2ú COVú1/2, (2.1.6)
где (S – áSñ)+ ‑ транспонированный вектор (S – áSñ), COV–ковариационнаяматрица размера N *N
COV =á(S – áSñ)(S – áSñ)+ ñ. (2.1.7)
Закон (2.1.6) можно рассматривать как закон распределения плотности вероятности помех H, так и самих случайных векторов состояний S.
В (2.1.6) и (2.1.7) áñ – операция математического ожидания, т.е. теоретического усреднения или усреднения по генеральной совокупности (см. подраздел «Статистики наблюдений …»); COV-1 – матица, обратная COV, úCOVú ‑ детерминант матрицы COV. Выражаясь конкретнее, если Sn есть “n”-ый компонент S, áSkñ есть «k»-ый компонент áSñ, а covnk есть «nk»-ый компонент COV, то
сovnk = snk = á(Sn – áSnñ)(Sk – áSkñ)ñ. (2.1.8)
Диагональный элемент
сovnn = D(Sn) = var(Sn) = sn2 = á(Sn – áSnñ)2ñ (2.1.9)
есть дисперсия (вариация) Sn, где sn называется среднеквадратичным или стандартным отклонением Sn от áSnñ. Если Sn и Sk статистически независимы, то covnk = 0 для " n ¹ k . В этом случае
pнор(S) = exp[–(S1 – áS1ñ)2/2s 12]/(2p)1/2s 1 ´ …
×exp[–(SN – áSNñ)2/2s N2]/(2p)1/2s N, (2.1.10)
т.е. многомерный нормальный закон распределения описывается произведением N одномерных нормальных законов
pнор(Sn) = exp[– (Sn – áSnñ)2/2s n2]/(2p)1/2s n . (2.1.11)
Нормальные законы распределений (одномерные и многомерные) широко используются при описании стохастических состояний ТП даже в тех случаях, когда не выполняются условия центральной предельной теоремы. Тогда распределение (2.1.6) является некоторой моделью некоего истинного распределения Prист(S).
Привлекательность распределений типа (2.1.6) связана с тем, что они являются параметрическими, т.е. зависят от конечного числа параметров áSñ, COV.
Наглядное представление нормальной двумерной плотности распределения для двумерного вектора состояний S =(S1, S2) приведено на рис. 2.1.3 в виде функции двух переменных (рис. 2.1.3а) и в виде диаграммы разброса случайных выборок (рис. 2.1.3б).
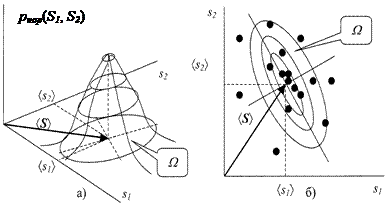
Рис. 2.1.3
Выборки нормально распределенной случайной величины имеют тенденцию попадать в одну область или кластер W.. Центр кластера определяется вектором áSñ среднего значения, а форма – ковариационной матрицей COV. Из (2.1.6) и рис. 2.1.3б следует, что точки постоянной плотности образуют эллипсоид (в многомерном случае – гиперэллипсоид), для которого квадратичная форма (S – áSñ)+ COV –1(S – áSñ) постоянна. Главные оси этого гиперэллипсоида задаются собственными векторами ковариационной матрицы COV.
Нормальное распределение обладает следующими важными свойствами:
- нормальная случайная величина S с математическим ожиданием áSñ и стандартным отклонением s с вероятностью близкой к 1 попадает в интервал (правило трех сигм)
(áSñ ‑ 3s) £ S £ (áSñ + 3s);
- если случайная величина S распределена по нормальному закону с математическим ожиданием áSñ и стандартным отклонением s, то
F(s) = Pr(S £ s) = Ф( 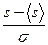 ), Pr(S > s) = 1 – Ф(
), Pr(S > s) = 1 – Ф( 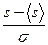 ),
),
где Ф – интеграл ошибок, определяемый (2.1.4) и (2.1.6).
Произвольный закон.
Истинное распределение может описываться совершенно произвольным законом. Во многих случаях закон распределения неизвестен, и его необходимо оценивать. Пусть p*(S) – оценка истинной плотности распределений pист(S). Будем искать такую оценку, которая обеспечивает минимизацию среднеквадратичной ошибки
СКО = ò.òò [p*(S) – pист(S)]2 d(N) S Þ min, (2.1.12)
где d(N) S = dS1 dS2 … dSN.
Разложим оценку p*(S) в ряд
p*(S) = 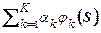 (2.1.13)
(2.1.13)
по системе ортонормированных функций j k(S). Ортонормированность означает
ò.òò j k(S) j m(S) d(N) S = 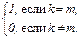 (2.1.14)
(2.1.14)
Подставив (2.1.13) в (2.1.12), получим
СКО = ò.òò [ 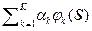 – pист(S)]2 d(N) S. (2.1.15)
– pист(S)]2 d(N) S. (2.1.15)
Необходимые условия минимума (2.1.15) заключаются в том, что
¶ СКО /¶ ak = ò.òò [ 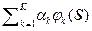 – pист(S)] j k(S) d(N) S = 0 для " k или
– pист(S)] j k(S) d(N) S = 0 для " k или
ak = ò.òò pист(S) j k(S) d(N) S = (1/M) 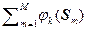 . (2.1.16)
. (2.1.16)
В (2.1.16) использована замена теоретического среднего значения функции j k(S) его выборочным средним (см. 2.2.3)
Таким образом, оценкой истинной плотности распределения является
p*(S) = (1/M) 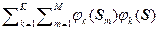 . (2.1.17)
. (2.1.17)
Оценка коэффициентов ak может быть получена рекуррентно. Так, если получена оценка (2.1.16) ak(M) по выборке объема M, то выражение для коэффициента при увеличении выборки на один объект имеет вид (см. 2.2.5)
ak(M+1) = [1/(M+1)] [ 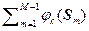 ] =
] =
= [1/(M+1)] [M ak(M) + j k(SM+1)]. (2.1.18)
Часто закон распределения приближают с помощью парзеновских окон (по имени статистика Парзена)
p*M(S) = (1/M) 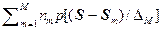 , (2.1.19)
, (2.1.19)
где функция окна p[(S – Sm)/DM] является некоторым распределением («ядром»), центрированным в Sm и обладающим шириной DM, зависящим от числа выборок M. Как правило, с ростом M ширина окна сужается. Величина nm соответствует количеству выборок, попавших в «точку» Sm. При M @ 100 парзеновское приближение практически сходится к истинному распределению.
2.2. Статистики наблюдений. Расчет статистик.
Статистикой наблюдаемого состояния S называют среднюю величину áfñ любой функции f [S] от наблюдений
áfñ = ò.òò pист(S) f [S] d(N) S. (2.2.1)
Нормальные законы распределения зависят лишь от статистик первого и второго порядка – средних значений áSñ наблюдений и их ковариаций COV (дисперсий s 1 , s 12… , s 1n, s n, …)
áSñ = ò.òò pнор(S) S d(N) S, (2.2.2)
COV = ò.òò pнор(S) (S – áSñ)(S – áSñ)+ d(N) S.
Выражение (2.2.1) определяет теоретическое среднее функции f [S], когда известна pист(S), как непрерывная функция S. На практике обычно наблюдают множество (ансамбль) {S} = = {S1, S2, …, Sm, …, SM} M различных значений или выборок (см. рис 2.1.3б) векторов состояний, которое порождает ансамбль {f [S]} = {f [S1], f [S2], …, f [Sm], …, f [SM]} разнообразных значений выборочных функций этих состояний. Тогда эмпирическое или выборочное среднее значение функции f [S] определяется выражением
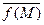 = (1/M)
= (1/M) 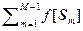 . (2.2.3)
. (2.2.3)
Например, эмпирические или выборочные значения среднего и ковариационной матрицы определяются выражениями
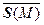 = (1/M)
= (1/M) 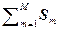 , (2.2.4)
, (2.2.4)
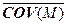 = [1/(M–1)]
= [1/(M–1)] 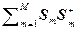 –
– 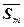
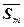 +.
+.
Оценка эмпирического или выборочного среднего значения функции f[S] может быть получена рекуррентно. Так, если получена оценка (2.2.3) 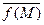 по выборке объема M, то выражение для среднего при увеличении выборки на один объект имеет вид
по выборке объема M, то выражение для среднего при увеличении выборки на один объект имеет вид
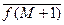 = [1/(M+1)] [
= [1/(M+1)] [ 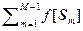 ] =
] =
= [1/(M+1)] [M 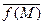 + f(SM+1)]. (2.2.5)
+ f(SM+1)]. (2.2.5)
Так, например, для среднего значения и ковариационной матрицы получим
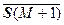 = [1/(M+1)] [M
= [1/(M+1)] [M 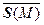 + SM+1], (2.2.6)
+ SM+1], (2.2.6)
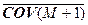 = [1/(M+1)] [M
= [1/(M+1)] [M 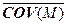 +
+
+ M 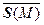
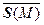 + + SM+1 S+M+1] – [1/(M+1)2] [M
+ + SM+1 S+M+1] – [1/(M+1)2] [M 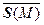 +
+
+ SM+1] [M 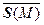 + SM+1]+.
+ SM+1]+.
Естественно, что задавая различные функции fk[S], где k = = 1, 2, …, K, возможно построить множество различных статистик. Однако только некоторые из них позволяют достаточно полно, как и сама плотность распределения pист(S), описать случайные наблюдения. Такие статистики называют достаточными статистиками. Для нормально распределенных случайных наблюдений их средние значения и ковариационные матрицы (дисперсии) являются достаточными статистиками.
Многие наблюдения, плотности вероятностей которых не подчиняются нормальному закону, могут быть описаны статистиками второго порядка – их средними значениями и ковариационными матрицами. Очевидно, что это возможно при достаточно хорошей аппроксимации (в смысле 2.1.12) истинных плотностей вероятностей pист(S) нормальными плотностями pнор(S).
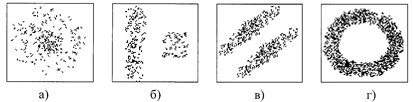
Однако встречаются случаи, когда такая аппроксимация принципиально невозможна. Так, на рис. 2.2.1 показаны четыре различных кластера данных, у которых одинаковые средние и матрицы ковариаций. Очевидно, что статистики второго порядка не в состоянии отобразить структуру приведенных наблюдений.
Рис. 2.2.1
Несмещенность, эффективность и состоятельность
статистических оценок. Расчет статистик.
Выборкой в статистике называют последовательность независимых одинаково распределенных случайных величин. Следует помнить, что любая из эмпирических оценок 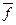 любой функции f[S] от наблюденийявляется случайной величиной. Все данные оценки производятся на конечном ряде выборок случайных величин (M = const), которые не исчерпывают их всевозможные значения, называемые генеральной совокупностью (M ® ¥). Поэтому будет всегда присутствовать ошибка, которую желательно свести к минимуму. Для этого используют некоторые критерии, которые позволяют минимизировать различия оценок функций, полученных для конечного ряда выборок и генеральной совокупности, т.е.
любой функции f[S] от наблюденийявляется случайной величиной. Все данные оценки производятся на конечном ряде выборок случайных величин (M = const), которые не исчерпывают их всевозможные значения, называемые генеральной совокупностью (M ® ¥). Поэтому будет всегда присутствовать ошибка, которую желательно свести к минимуму. Для этого используют некоторые критерии, которые позволяют минимизировать различия оценок функций, полученных для конечного ряда выборок и генеральной совокупности, т.е. 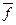 и теоретического математического ожидания á f ñ.
и теоретического математического ожидания á f ñ.
Несмещенными называются такие оценки, математические ожидания которых равняются теоретическим математическим ожиданиям, полученным при использовании генеральной совокупности.
Например, выборочные среднее и ковариационная матрица (2.2.4) являются несмещенными оценками теоретических среднего и ковариационной матрицы.
Эффективными являются оценки выборочного среднего с минимально возможными дисперсиями.
Только выражение (2.2.3) дает несмещенную и эффективную оценку среднего значения функции f [S].
Состоятельными называются такие оценки, которые дают точные значения для больших выборок (M), независимо от входящих в них конкретных наблюдений.
Правила расчет статистик второго порядка.
Правила расчета ковариаций.
Правило 1:
Если Y = V + W, то
cov(X,Y) = cov(X, V + W) = cov(X, V) + cov(X, W).
Правило 2:
Если Y = a Z, где a – константа, то cov(X,Y) = a cov(X, Z).
Правило 3:
Если Y = a , где a – константа, то cov(X,Y) = 0.
Пользуясь этими основными правилами, можно упрощать значительно более сложные выражения с ковариациями. Например, если Y = U + V + W , то пользуясь правилом 1 и разбив Y на две части (U и V + W), получим
cov(X,Y) = cov(X,U+V+W) = cov(X,U)+cov(X,V+W) =
= cov(X,U) + cov(X,V) + cov(X, W).
Другой пример: Если Y = a + b Z, где a и b – константы, то, пользуясь последовательно правилами 1, 3, 2, получим
cov(X,Y) = cov(X,a)+cov(X,bZ)=0+cov(X,bZ)=bcov(X,Z).
Правила расчета дисперсий.
Правило 1:
Если Y = V + W, то var(Y) = var(V) + var(W) + 2cov(V, W).
Правило 2:
Если Y = a Z, где a – константа, то var(Y) = a2 var(Z).
Правило 3:
Если Y = a , где a – константа, то var(Y) = 0.
Правило 4:
Если Y = Z + a, где a – константы, то var(Y) = var(Z).
Как следует из определения дисперсии var(X) = cov(X,X).
Правила расчета коэффициентов корреляций.
Теоретический и выборочный коэффициент корреляции случайных величин X и Y задаются выражениями
rXY = sXY / (s 2X s 2Y )1/2, (2.2.7)
rXY = cov(X,Y)/ [var(X) var(Y )]1/2.
Для векторов X = (X1, X2, …, XM) и Y = (Y1, Y2, …, YM) часто используют выборочный коэффициент корреляции, определяющий косинусу угла между ними (см. рис. 2.2.2)
rXY = cosj = (åMm=1 Xm Ym) / (åMm=1 X 2m)1/2 (åMm=1 Y 2m)1/2.
(2.2.8)
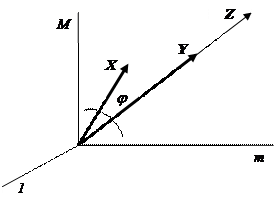 |
Рис. 2.2.2
Данный коэффициент совпадает с выборочным коэффициентом корреляции (2.2.7) для M выборок случайных величин X и Y , у которых áXñ = áYñ = 0.
Коэффициент корреляции (2.2.8) в некоторой степени описывает меру связи между случайными величинами X и Y. Величина связи изменяется в пределах -1 £ rXY £ 1.
Однако мера связи (2.2.8) не вполне корректно выявляет «силу» связи. Так, например, из рис. 2.2.2 видно, что случайные величины X и Y, а также X и Z имеют одинаковые коэффициенты корреляции rXY = rXZ , хотя вектора X и Y «ближе» друг к другу, чем вектора X и Z.
Более правильно «силу» связи описывает модифицированный коэффициент корреляции
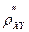 = 2cov(X,Y)/ [var(X) + var(Y )] = (2.2.9)
= 2cov(X,Y)/ [var(X) + var(Y )] = (2.2.9)
= (2åMm=1 Xm Ym) / [(åMm=1 X 2m) + (åMm=1 Y 2m)].
Из (2.2.9) видно, что 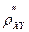 ® 0 при удалении Y от X в направлении Z, что говорит об ослаблении связи случайных величины X и Y. Это не описывается коэффициентом rXY .
® 0 при удалении Y от X в направлении Z, что говорит об ослаблении связи случайных величины X и Y. Это не описывается коэффициентом rXY .
Расчет статистик высшего порядка.
Коэффициент асимметрии.
Коэффициент асимметрии (или скоса) Пирсона применяется для проверки репрезентативности однородной выборки. Репрезентативность означает насколько состоятельно выборка представляет генеральную совокупность.
Пусть, например, генеральная совокупность некоторой случайной величины X опиcывается нормальным законом. Произведено M выборок {X1, X2, …, Xm, …, XM} данной величины. Тогда коэффициент асимметрии определяется, как
SkX = 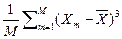 /
/ 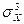 . (2.2.10)
. (2.2.10)
Если выборки однородны и репрезентативны, то коэффициент асимметри SkX близок к 0. В случае положительного / отрицательного значения коэффициента (положительного / отрицательного скоса), выборки представляют часть генеральной совокупности, расположенную справа / слева от ее среднего значения.
Некоторые статисты (В.В. Швырков) предлагают использовать для определения коэффициента асимметрии статистику более высокого порядка
SkX = 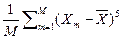 /
/ 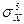 , (2.2.11)
, (2.2.11)
которая более правильно описывает «скошенные» данные.
Коэффициент эксцесса.
Данный коэффициент определяется выражением
eX = [ 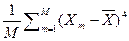 /
/ 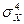 ] – 3. (2.2.12)
] – 3. (2.2.12)
Если значение эксцесса eX больше 0, выборочное распределение более остроконечно, чем нормальное. В случае отрицательного эксцесса, выборочное распределение более полого, чем нормальное. Равенство эксцесса 0 означает, что выборочные значения однородно и репрезентативно представляют нормальную генеральную совокупность данных.
2.3. Нечеткое описание неопределенностей
технологических процессов.
Теоретический подход.
Многие неопределенности могут и не подчиняться нормальному или иным известным законам распределений. Типична ситуация, когда наблюдения «разбросаны» в некоторой ограниченной области W, а закон их распределения неизвестен. Такие наблюдения могут быть описаны нечеткой функцией m(S) принадлежности, нормированной на 1, т.е.
ò.òò m(S) d(N) S = 1. (2.3.1)
Возьмем в качестве меры неопределенности задания области W энтропию
Э = – ò.òò m(S) lnm(S) d(N) S. (2.3.2)
W
Будем считать, что информация о наблюдении Sзадается в виде
ò.òò m(S) d(N) S = 1, (2.3.3)
áfkñ = ò.òò m(S) fk[S] d(N) S, k = 1, 2, …, K.
Наша цель заключается в таком задании нечеткой функцией m(S) принадлежности, чтобы величина энтропии при выполнении условий (2.3.3) была минимальной. Использование неопределенных множителей l0, l1, …, lK позволяет построить вспомогательную функцию Лагранжа
L = –ò.òò m(S){lnm(S) – åK lk fk[S]}d(N) S – åK lk áfkñ , (2.3.4)
W k=0 k=0
где f0[S] = 1 и áf0ñ = 1 для " S Î W.
Приравняв нулю все частные производные от L по m(S), получим искомую функцию принадлежности
m(S) = exp[ 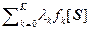 – 1]. (2.3.5)
– 1]. (2.3.5)
В (2.3.5) K+1 параметров l0, l1, …, lK следует выбирать так, чтобы удовлетворить условиям (2.3.3).
Пример 2.3.1. Пусть, например, все скалярные компоненты Sn (n = 1, 2, …, N) вектора S ТП независимы, а их одномерные области Wn заданы граничными значениями an и bn так, что an < Sn < bn. Поскольку W = W1 ´ W2 ´ … ´ WN, то m(S) = min{m(S1), m(S2), …, m(SN)}. Тогда из (1.5.5) следует, что
m(S) = min{m(S1), m(S2), …, m(SN)} = exp[l0 – 1]. (2.3.6)
Так как
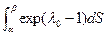 = 1, то exp[l0 – 1] (b – a) = 1.
= 1, то exp[l0 – 1] (b – a) = 1.
Отсюда получим
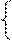 m(S) = min{1/(b1 – a1), …, 1/(bN – aN)}, если S Î W,
m(S) = min{1/(b1 – a1), …, 1/(bN – aN)}, если S Î W,
0, если S Ï W. (2.3.7)
Эмпирический подход.
Закон нечеткого распределения состояний может быть аппроксимирован феноменологической параметрической зависимостью, например
m(S) = a exp[–½S – áSñ ½b/g], (2.3.8)
где a, b, g – параметры нечеткого распределения, которые описывают как остроту, так и степень «размытия» состояний.
Одномерные нечеткие функции принадлежности приведены вместе с одномерным нормальным распределением на рис. 2.3.1. Нормальное распределение построено при s = 2, а нечеткие – при b = 5, g = 1000 (нечеткое 1) и b = 0,8, g = 1 (нечеткое 2) соответственно. Для наглядности (равенства максимальных значений) a = 1/( 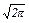 s), а áSñ = 0.
s), а áSñ = 0.
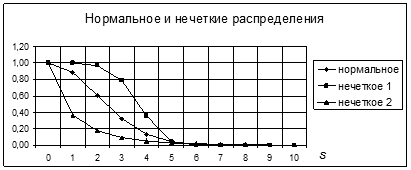
Рис. 2.3.1
Нечеткая функция принадлежности (2.3.8) особенно удобна при эмпирическом оценивании ее параметров. В качестве примера рассмотрим методику эмпирического оценивания характера неопределенности пищевого сырья, разработанную на базе мясного пищевого сырья.
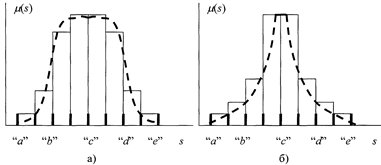 |
Пример2.3.2. Для оценки характера неопределенности пищевого биосырья были проанализированы его базовые показатели (содержание влаги, белка, жира, водосвязывающая способность, цвет) и оценены реперные точки нечетких функций принадлежности значений данных показателей областям, заключенным между минимальными и максимальными значениями. Совокупность данных реперных точек и частоты соответствующих показателей в интервалах между реперными точками приведены на рисунке 2.3.2.
Рис. 3.3.2
Соответствующие гистограммы частотных распределений, расклассифицированы экспертами на два характерных типа. На рис. 2.3.2 показаны девять реперных точек, разделяющих области значений показателей биосырья на восемь равных интервалов. Столбик над каждым интервалом показывает относительное количество биосырья, показатели которого попадают в соответствующий интервал.
Дополнительные исследования показали, что оба типа частотных гистограмм могут быть аппроксимированы нечеткой феноменологической функцией принадлежности (2.3.8) (см. пунктирные кривые на рисунке 2.3.2).
Наряду с (2.3.8), существует также множество других параметрических нечетких феноменологических функций принадлежности, с помощью которых возможно описывать «размытые» эмпирические данные, например
m1(S) = exp{– a [exp(–½S– áSñ½2/2b 2) – 1]2}, (2.3.9)
m2(S) = a /{a + [1 – exp(–½S– áSñ½2/2b 2)]N},
m3(S) = a /{a +[åNm=1 (Sm – áS mñ)2] N / (2b 2) N }.
где параметры a и b определяют остроту и ширину нечетких функций принадлежности.
В качестве примера одномерные (N = 1) нечеткие функции принадлежности (2.3.9) приведены на рис. 2.3.3 для a = 1000, b = 20и a = 0,001, b = 20соответственно. При этом áSñ = 0.
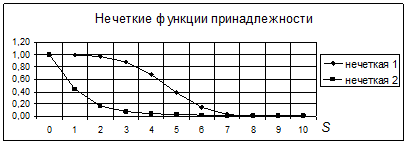 |
Легко заметить, что нечеткие функции принадлежности (2.3.9) могут быть также использованы для эмпирической оценки разных типов распределений, представленных на рисунке 2.3.2.
Рис. 2.3.3
Разделение вероятностных и нечетких методов описания неопределенности ТП на практике носит условный характер. Вероятностным методам следует отдавать предпочтение, если существует возможность проведения большого количества (@ 300) повторных наблюдений, а помехи при каждом наблюдении являются независимыми и для различных наблюдений компенсируют друг друга. В противном случае неопределенность ТОносит нечеткий характер.
2.4. Сравнение состояний технологических процессов.
Меры сравнения состояний технологий.
Метрические меры.
При мониторинге ТП с помощью различных СК возникает проблема сравнения их состояний, группировок (объединений) состояний, различения состояний, распознавания состояний. Для этого используют некоторые меры различия и, в первую очередь, метрические меры.
Напомним, что мы описываем состояния ТПс помощью векторов S = {S1, S2, …, Sn, …, SN} состояний, заданных в N-мерном евклидовом пространстве. Одним из основных свойств N-мерных евклидовых пространств является то, что в них для любых двух «точек», заданных S1 и S2, определена метрика (или расстояние)
r (S1, S2)= ú S1 – S2ú = [(S1 – S2)+ (S1 – S2)]1/2 =
= [ 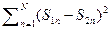 ]1/2 , (2.4.1)
]1/2 , (2.4.1)
удовлетворяющая трем условиям:
1) r (S1, S2) ³ 0, причем r (S1, S2) = 0 тогда и только тогда,
когда S1= S2;
2) для любых «точек» S1и S2 имеет место равенство
r (S1 , S2) = r (S12, S1);
3) для любых трех «точек» S1, S2 и S3 выполняется правило, называемое неравенством треугольника
r (S1 , S3) ³ r (S1 , S2) + r (S2 , S3).
Иногда удается определить функцию r, удовлетворяющую этим условиям, на парах элементов некоторого множества, которое не является евклидовым пространством. Подобное множество называется метрическим пространством, а функция r – его метрической мерой.
Безразмерную метрическую меру r, определяемую соотношением
r 2(S, áSñ) = (S – áSñ)+ COV-1(S – áSñ) (2.4.2)
и задающую расстояние от S до некоторого кластера с центром áSñ и ковариационной матрицей COV, называют махаланобисовым расстоянием. В частном случае (2.1.10), махаланобисово расстояние определяется соотношением
r 2 = ån (Sn – áSnñ)2/2s n2= (S1– áS1ñ)2 / 2s 12 + …+ (2.4.3)
+ (SN – áSNñ)2 / 2s N2.
Выражения (2.4.1 и 2.4.3) возможно обобщить, вводя взвешенное евклидово расстояние между произвольными векторами S1 и S2
r 2(S1, S2) = (S1 – S2)+ D+D(S1 – S2) = ån dn2 (S1n – S2n)2 =
= d12 (S11– S21)2 + … + dN2 (S1N – S2N )2, (2.4.4)
D = 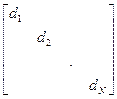 ,
,
где dn – некоторые произвольные весовые коэффициенты. Данные весовые коэффициенты позволяют, например, свести различные фазовые координаты ТП к одной размерности или вообще – к безразмерным величинам.
Вполне очевидно, что любую монотонную функцию f(r) от метрической меры также можно рассматривать как некоторую меру различия. Например, f(r) = r 2. Однако следует подчеркнуть, что не все такие функции могут служить метрическими мерами в смысле рассмотренных выше трех условий .
Каждой метрической и не метрической мере, определяющей меру различия между векторами, может быть поставлена в соответствие и мера их близости или сходства.
Неметрические меры.
Раскроем выражение (2.4.4) в следующем виде
r 2(S1 , S2)= (S1 – S2)+ D+D(S1 – S2) = (2.4.5)
= S1+ D+D S1 + S2+ D+D S2 – 2 S1+ D+D S2 .
Очевидно, что для векторов с фиксированными квадратами их длин S1+ D+D S1 и S2+ D+D S2 мера различия тем меньше, чем больше величина их скалярного произведения S1+ D+D S2. Поэтому скалярное произведение векторов можно рассматривать как некоторую неметрическую меру их сходства.
На практике широко используют следующие неметрические меры сходства, определяемые нормированными скалярными произведениями:
1) Классический коэффициент корреляции (косинус угла
между векторами, см. 2.2.8, стр. 39)
m(S1 , S2) = S1+D+D S2 /(S1+D+D S1)1/2(S2+D+D S2) 1/2, (2.4.6)
2) мера Танимото
m(S1 , S2) = S1+D+D S2 /(S1+D+D S1 + S2+D+D S2 – (2.4.7)
– S1+D+D S2),
3) модифицированный коэффициент корреляции (см.2.2.9)
m(S1 , S2) = 2 S1+D+D S2 /(S1+D+D S1 + S2+D+D S2). (2.4.8)
Все приведенные нормированные меры сходства равны 1 при S1= S2, что удобно для их содержательной интерпретации. Например, на их основании могут быть введены нормированные меры различия или несходства
mсх(S1, S2) = [1 + mнесх(S1, S2)]-1 . (2.4.9)
Обратная зависимость не всегда справедлива. Однако для
mнесх < 1 на основании (2.4.9) можно определить
mнесх(S1, S2) @ 1 – mсх(S1, S2). (2.4.10)
Нормированные меры различия, как функционалы метрических мер r (2.4.1 ¸ 2.4.4), отражают степень выраженности (или просто выраженность) отклонений векторов состояний ТП от некоторых заданных векторов состояний.
Наряду с (2.4.6 ¸ 2.4.8) возможно обобщить подход к мерам сходства. Так, рассмотренные в (2.3.9, стр. 44) распределения для нечеткого описаний ТП также являются неметрическими мерами сходства. Данные меры сходства, определяющие нечеткие функции принадлежности, имеют острые пики (m @ 1) при S1@ S2 и быстро спадают (m @ 0) при S1 ¹ S2 (см. рис. 2.3.3). Такие быстроспадающие меры сходства будем называть резонансными мерами. Они необходимы для оптимального различения состояний ТП.
Сравнение технологий в фазовых пространствах.
Будем описывать состояние ТП в каждый дискретный момент времени t с помощью вектора St, где t = 1, 2, … , T. Будем сравнивать различные ТП путем как прямого сравнения их траекторий (ТР) в фазовом пространстве, так и косвенного сравнения их обобщенных показателей (функционалов), однозначно определяемых данными ТР.
Прямое сравнение траекторий технологий.
Пусть в фазовом пространстве ТП заданы две ТР: {St} и {S*t}, t = 1, 2, … , T. Тогда метрическую меру различия данных ТР зададим в виде
r2å= 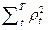 =
= 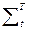 (St – S*t)+ D+D(St – S*t) = (2.4.11)
(St – S*t)+ D+D(St – S*t) = (2.4.11)
= 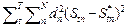 .
.
Возможно ввести более чувствительный критерий, учитывающий сравнение скоростей изменения ТР
Dr2å= 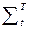 ½D (St+1 – S*t+1) – D (St – S*t)½2 . (2.4.12)
½D (St+1 – S*t+1) – D (St – S*t)½2 . (2.4.12)
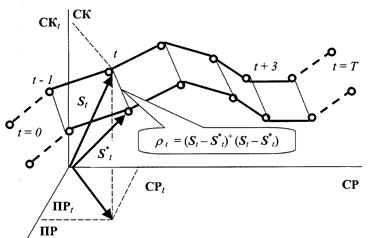 |
Для наглядности меры сравнения ТРпроиллюстрированы на рисунках 2.4.1 и 2.4.2.
Рис. 2.4.1
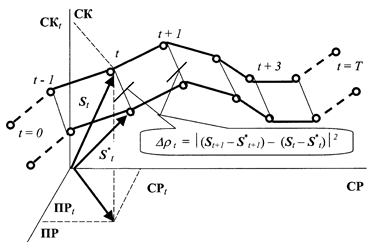 |
Рис. 2.4.2
Неметрическую меру сходства данных ТР зададим в виде
m å = 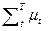 , (2.4.13)
, (2.4.13)
где меры сходства mt векторов состояний для каждого дискретного момента времени t могут быть определены, например, соотношениями (2.4.6 ¸ 2.4.8, 2.3.9).
Меры (2.4.11 ¸ 2.4.13) позволяют выбрать из всевозможных ТР ТПнаиболее близкую к заданной (оптимальной). Для такой искомой ТР должны быть выполнены следующие условия
r å Þ min, m å Þ max. (2.4.14)
Введенные меры сравнения не позволяют выбрать саму оптимальную ТР {S*t} среди возможных. Они удобны лишь для оптимального выбора ТР, наиболее близких к заданной. Важнейшим вопросом методологии сравнительного анализа ТП является формализация выбора оптимальной ТР ТП, соответствующей данной технологии. Такой выбор осуществляется на основе действующих стандартов ТП.
Косвенное сравнение технологий по траекторным
функционалам.
Введем для каждой ТР {St} (t = 1, 2, … , T) ТП траекторные функционалы – функционалы, определяемые формами ТР.
1) Функционал числа K ТОП
ФK ({St}) = K £ T. (2.4.14)
2) Функционал продолжительности ТП
ФT ({St}) = T = 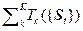 , (2.4.15)
, (2.4.15)
где Tk ({St}) – продолжительность «k»-ой ТОП.
3) Функционал затрат на осуществление ТП
ФЗ ({St}) = 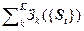 . (2.4.16)
. (2.4.16)
Если все ТОП затратно-эквивалентны, то Зk({St}) = З, а
ФЗ({St}) = K З.
4) Функционал сырьевых и продуктовых потерь
ФП ({St}) = 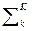 [СПk ({St}) + ППk ({St})], (2.4.17)
[СПk ({St}) + ППk ({St})], (2.4.17)
где СПk ({St}) – сырьевые потери на «k»-ой ТОП, а ППk ({St}) –продуктовые потери.
5) Функционалы показателей характеристик потребительских свойств продукта, получаемого, например, путемсмешивания ингредиентов
ФX = 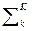 Пnk Mk, n = 1, 2, ..., N, (2.4.18)
Пnk Mk, n = 1, 2, ..., N, (2.4.18)
где Пnk (k = 1, 2, ..., К) – «n»-ые показатели характеристик конкретных ингредиентов, приходящихся на единицу массы, а Mk – массы (или концентрации) исходных сырьевых ингредиентов, К – количество ингредиентов в продукте, N – количество потребительских свойств.
Возможно также ввести «кинематические» функционалы.
6) Функционал средней скорости ТП
ФC = (1/K) 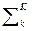 ½DSk+1 – DSk½/ Tk .(2.4.19)
½DSk+1 – DSk½/ Tk .(2.4.19)
7) Функционал среднего ускорения ТП
ФУ = (1/K) 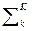 ½DSk+1 – 2DSk – DSk-1)½/T 2k . (2.4.20)
½DSk+1 – 2DSk – DSk-1)½/T 2k . (2.4.20)
Сравнение технологий можно осуществить на основе сравнения соответствующих функционалов.
Будем называть рассмотренные функционалы (1 ¸ 7) локальными функционалами. Их совокупность порождает многомерное пространство глобального функционала. В данном пространстве каждой конкретной траектории {S*t} ТП будет отвечать точка, определяемая соответствующим вектором глобального функционала (см. рис. 2.4.3)
Фå ({S*t}) = {ФK , ФT , ФЗ , ФП , ФX , ФC , ФУ}. (2.4.21)
Ввиду «размытости» ТР реальных ТПв пространстве глобального функционала, им будет отвечать некоторая «размытая» область Wå , как показано на рисунке 2.4.3.
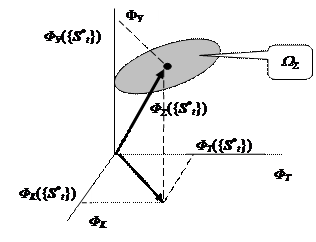 |
Рис. 2.4.3
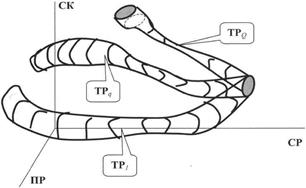 |
В фазовом пространстве {СР, СК, ПР} Q различным ТП одной и той же технологииили различнымтехнологиямбудут отвечать трубки (ТР) их траекторий, как показано на рисунке 2.4.4.
Рис. 2.4.4
Смысл иллюстрации заключается в том, что при различных условиях приложения технологий (различные характеристики исходного сырья, наличие различных возмущающих воздействий) получают продукт, который удовлетворяет заданным требованиям.
В пространстве глобального функционала траекториям различных технологий, приведенным на рисунке 2.4.4, будут соответствовать различные нечеткие области Wå(q) глобальных функционалов, где q =1, 2, …, Q. В общем случае данные области могут пересекаться, как показано на рис. 2.4.5.
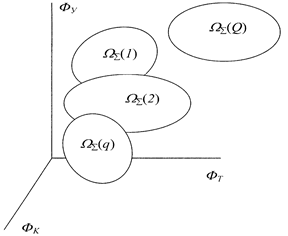 |
Задача заключается в выборе такой функциональной области Wå(q*) и, тем самым, технологии, которая удовлетворяет заданным оптимизационным критериям.
Рис. 2.4.5
Глобальные и локальные критерии сравнения технологий
по траекторным функционалам.
Глобальная оптимизация технологий.
Введем скалярный глобальный оптимизационный критерий в
виде выпуклой комбинации локальных функционалов
Фå = pK ФK + pT ФT + pЗ ФЗ + pП ФП + pХ ФX + pС ФC + pУ ФУ ,
pK + pT + pЗ + pП + pХ + pС + pУ = 1, (2.4.22)
где все локальные функционалы F – безразмерные, а соответствующие им p – весовые коэффициенты. Безразмерная величина функционала получается путем деления значения функционала на единицу его размерности.
Естественно потребовать, чтобы глобальный критерий (2.4.22) стремился к минимальному значению (Få ® min) для оптимальной технологии.
Сами весовые коэффициенты (p) возможно выбрать экспертным путем, придавая наибольший (наименьший) вес тому или иному локальному функционалу. При отсутствии априорной информации весовые коэффициенты одинаковы.
В глобальном функциональном пространстве выражение (2.4.22) описывает гиперплоскость, как показано на рис. 2.4.6.
| Дата добавления: 2016-06-02; просмотров: 694; |
Генерация страницы за: 0.296 сек.
