ПОЛИТРОПИЧЕСКИЕ ПРОЦЕССЫ.
Обычно рассматривают процессы, в ходе которых газ подчиняется, кроме уравнения состояния, некоторому дополнительному условию. Соответственно различают изотермический, изохорный, изобарный и адиабатный процессы. (Напомним, что адиабатным называется процесс, происходящий без теплообмена с внешней средой.) Оказывается, что все перечисленные процессы являются частичными случаями политропического процесса, в ходе которого, по определению, остается постоянной теплоемкость тела.
Найдем уравнение политропы, т.е. уравнение, связывающие параметры идеального газа при политропическом процессе. Обозначим теплоемкость тела в ходе конкретного политропического процесса  . Тогда из первого начала термодинамики
. Тогда из первого начала термодинамики 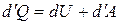 следует, что (
следует, что ( 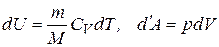 )
)
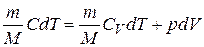 . (7.20)
. (7.20)
Преобразуем (7.20) к виду:
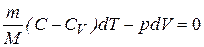 . (7.21)
. (7.21)
Выразим 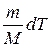 из уравнения состояния:
из уравнения состояния:
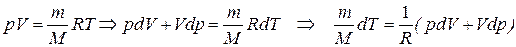 , (7.22)
, (7.22)
и подставим в (7.21):
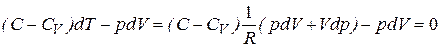 . (7.23)
. (7.23)
Умножим (7.23) на 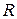 и перегруппируем слагаемые:
и перегруппируем слагаемые:
 . (7.24)
. (7.24)
Разделим (7.24) на 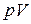 и учтем что
и учтем что 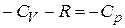 :
:
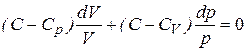 . (7.25)
. (7.25)
После интегрирования (7.25) получим соотношение:
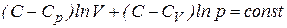 . (7.26)
. (7.26)
Разделим обе части (7.26) на 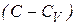 :
:
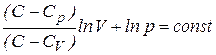 . (7.27)
. (7.27)
Обозначим:
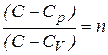 . (7.28)
. (7.28)
Тогда (7.27) можно записать в виде
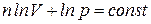 или
или 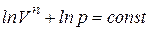 . (7.29)
. (7.29)
Потенцирование (7.29) (надо возвести число е в степень выражения в левой части) дает соотношение:
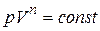 . (7.30)
. (7.30)
Уравнение (7.30) есть искомое уравнение политропы, а величина n называется показателем политропы.
Значение 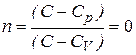 соответствует
соответствует 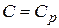 , т.е. изобарному процессу.
, т.е. изобарному процессу.
Значение 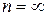 соответствует нулевому знаменателю в (7.28), т.е.
соответствует нулевому знаменателю в (7.28), т.е. 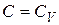 , а значит изохорному процессу.
, а значит изохорному процессу.
Значение 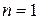 соответствует закону Бойля-Мариотта, т.е. изотермическому процессу. Действительно, при изотермическом процессе
соответствует закону Бойля-Мариотта, т.е. изотермическому процессу. Действительно, при изотермическом процессе 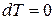 по определению процесса, а сообщаемое тепло
по определению процесса, а сообщаемое тепло 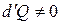 . Следовательно, теплоемкость при изотермическом процессе
. Следовательно, теплоемкость при изотермическом процессе 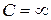 , что соответствует
, что соответствует 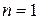 .
.
При адиабатном процессе 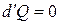 при
при 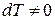 , а значит теплоемкость в ходе такого процесса
, а значит теплоемкость в ходе такого процесса 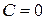 . В этом случае показатель политропы оказывается равным
. В этом случае показатель политропы оказывается равным 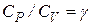 и, следовательно, уравнение адиабаты имеет вид:
и, следовательно, уравнение адиабаты имеет вид:
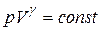 . (7.31)
. (7.31)
Уравнение адиабаты (7.31) называется уравнением Пуассона. Это уравнение описывает обратимый адиабатный процесс (конкретные точные значения параметров), а значит процесс квазистатический. Поскольку в природе не существует не проводящих тепло тел, то достаточно близкими к адиабатному могут быть только весьма быстро протекающие процессы. Примером такого процесса может быть сжатие и расширение, происходящее в данной точке газа при распространении в нем звуковой волны. При этом состояние газа в малом объеме приближается к равновесному, и при распространении волны в газе происходит адиабатный процесс.
Дата добавления: 2016-06-02; просмотров: 798;
