ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Рассмотрим теперь общий случай: пусть имеется система из 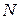 частиц, взаимодействующих между собой посредством консервативных сил, и одновременно находящихся под действием внешних консервативных и неконсервативных сил.
частиц, взаимодействующих между собой посредством консервативных сил, и одновременно находящихся под действием внешних консервативных и неконсервативных сил.
Получим выражение для работы, совершаемой над частицами системы, при перемещении системы из одного положения в другое и одновременном изменении конфигурации системы. Обозначим работу внешних консервативных сил 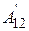 . Эта работа равна убыли потенциальной энергии во внешнем поле сил:
. Эта работа равна убыли потенциальной энергии во внешнем поле сил:
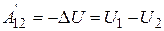 . (3.55)
. (3.55)
Для работы внутренних консервативных сил при изменении конфигурации системы справедливо аналогичное выражение:
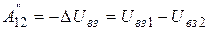 . (3.56)
. (3.56)
Обозначим работу неконсервативных сил 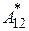 . Вспомним, сформулированное нами ранее утверждение: суммарная работа идет на приращение кинетической энергии системы. Тогда можно записать соотношение:
. Вспомним, сформулированное нами ранее утверждение: суммарная работа идет на приращение кинетической энергии системы. Тогда можно записать соотношение:
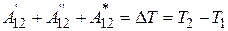 . (3.57)
. (3.57)
Подставим в левую часть выражения для работы консервативных сил:
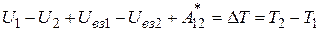 , (3.53)
, (3.53)
Или, после перегруппировки слагаемых по индексам,
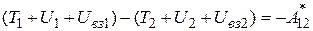 . (3.54)
. (3.54)
Обозначим сумму 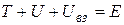 . Эта сумма, по определению, представляет собой полную механическую энергию системы. Тогда из (3.54) следует, что приращение полной энергии системы
. Эта сумма, по определению, представляет собой полную механическую энергию системы. Тогда из (3.54) следует, что приращение полной энергии системы
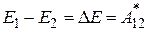 (3.55)
(3.55)
равно работе неконсервативных сил.
В частном случае, при их отсутствии, полная энергия не изменяется:
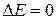 . (3.56)
. (3.56)
Таким образом, полная механическая энергия системы материальных точек, находящихся под действием только консервативных сил, остается постоянной. Это утверждение называют законом сохранения механической энергии.
Дата добавления: 2016-06-02; просмотров: 582;
