Элементарные звенья и их характеристики

Вообще же звеном называют математическую модель элемента, соединения элементов или любой части системы. Звенья, как и системы, могут описываться дифференциальными уравнениями довольно высокого порядка, и в общем случае их передаточные функции могут быть записаны в виде

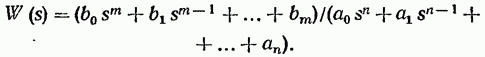
Но всегда их можно представить как соединения типовых или элементарных звеньев, порядок дифференциальных уравнений которых не выше второго.

Из курса алгебры известно, что полином произвольного порядка можно разложить на простые множители — множители вида

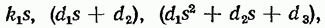
поэтому передаточную функцию (2.41) можно представить как произведение простых множителей вида (2.42) и простых дробей вида

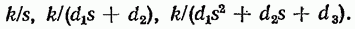
Звенья, передаточные функции которых имеют вид простых множителей (2.42) или простых дробей (2.43), называют типовыми или элементарными звеньями.

Прежде чем переходить к изучению элементарных звеньев, вспомним формулы для модуля и аргумента комплексного числа. Пусть комплексное число представлено в виде отношения двух произведений комплексных чисел

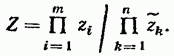
Так как то для модуля и аргумента комплексного числа имеем

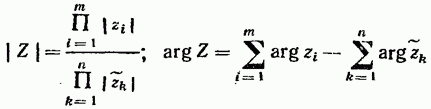
Таким образом, справедливо следующее правило модулей и аргументов комплексных чисел: модуль комплексного числа, представленного в виде отношения двух произведений комплексных чисел, равен отношению произведения модулей сомножителей числителя к произведению модулей сомножителей знаменателя, а его аргумент — разности суммы аргументов сомножителей числителя и суммы аргументов сомножителей знаменателя.