Прогнозирование и нормирование простоя вагонов на станции
Основными факторами, от которых зависит среднее время нахождения вагонов на станции, являются техническое оснащение станции, технология работы и нагрузка, т. е. объем работы с соответствующим ему уровнем неравномерности поступления вагонов и поездов. Под прогнозированием простоя вагонов понимается установление среднего времени нахождения вагона на станции за некоторый предстоящий календарный период в зависимости от объема работы при заданном уровне технического развития, технологии и управления. При этом техническое оснащение и технология работы в течение этого периода, как правило, остаются постоянными. Если параметры технологии, технического развития изменяются, то перерассчитывается и прогноз норм простоя вагонов. Нормирование – это практическое использование результатов прогнозирования для конкретных периодов времени конкретной станции, если прогнозные нормы утверждены в качестве обязательных для выполнения. Основные требования к методам прогнозирования и нормирования – научная обоснованность, достаточная адекватность реальным условиям работы и точность результатов. Однако следует отметить, что метода, полностью отвечающего всем указанным требованиям, пока не существует. Поэтому используются несколько методов, которые можно объединить в следующие группы – графические, табличные, аналитические и имитационные.
Простои вагонов могут быть рассчитаны на основе построения графической модели работы станции (суточного план-графика), представляющей собой символьное изображение на специальном бланке основных производственных процессов, протекающих в подсистемах
станции в их взаимосвязи и взаимозависимости. В графической модели отражаются моменты прибытия и отправления поездов, занятие ими приемо-отправочных путей, процессы обработки составов в парках приема и отправления, накопление вагонов в сортировочном парке, работа горки и вытяжных путей с детализацией ее по отдельным элементам и локомотивам, процессы обработки местных вагонов, их подача, уборка, погрузка, выгрузка.
Благодаря учету занятости основных элементов станции (путей, стрелочных улиц, отдельных стрелок) в модели отражаются враждебные маршруты и связанные с ними межоперационные простои подвижного состава и сортировочных устройств. Практически имеется полная возможность отразить все взаимодействующие технологические процессы, их влияние друг на друга, найти наиболее загруженные каналы и элементы схемы станции и наметить меры их усиления и разгрузки.
По графической модели подсчитываются все основные показатели работы станции: нормы простоя транзитных вагонов без переработки и с переработкой, в общем, и с расчленением по элементам, простоя местного вагона, в том числе приходящегося на одну грузовую операцию, коэффициент сдвоенных операций, коэффициенты использования маневровых локомотивов по времени и их производительность в вагонах, показатели надежности работы станции и основных элементов и т. д. В итоге получается набор показателей, характеризующий работу станции.
Недостатком этого метода является значительная трудоемкость подготовки исходной информации и особенно составления графической модели. В прошлом исходили из предпосылки, что достаточно точные результаты можно получить на основе построения модели на одни сутки (отсюда и название суточный план-график работы станции), но
исследования показали, что это не так. Достоверные результаты получаются лишь при моделировании заботы станции на 10-15 сут.
Недостатком графической модели является также использование для ее разработки исходной информации, заимствованной из прошлого, т.е. фактического подвода поездов, разложения их составов и т.д. В этом случае графическая модель получается как бы идеальной копией фактической работы станции за какой-то период. Очевидно, что случайные факторы, имевшие место в тот период, находят свое отражение в фактических показателях работы станции, но не в графической модели.
Существует рекомендация более строгого отбора информации: выбор «характерных» периодов, отсев вызывающих сомнение суток и т.д. Наиболее перспективной, научно обоснованной подготовкой информации является подготовка на основе исследования и обобщения фактических данных методами вероятностей и математической статистики. В этом случае показатели работы, полученные по графической модели, будут иметь более высокую степень соответствия фактическим условиям работы станции.
В начале 70-х годов во ВНИИЖТе разработан так называемый метод табличного моделирования, сущность которого заключается в последовательном отражении в специальных графах таблицы интервалов прибытия, начала и конца обработки, взятия составов из ПП для расформирования; интервалов вывода составов в ПО, отправления поездов со станции. Расчеты выполняют раздельно по каждой подсистеме без учета влияния работы одной подсистемы на другие.
Метод табличного моделирования исходит из предпосылки, что каждый оставшийся на обслуживание состав, переходя из одного расчетного интервала в следующий, в среднем находится в системе обслуживания в течение всего расчетного интервала. Отсюда, табличный метод расчета заключается в последовательном определении переходящего остатка составов на каждый последующий расчетный интервал с дальнейшим суммированием составо-минут простоя за весь расчетный период.
Форма расчетной таблицы применительно к подсистеме ВхУ-ПП-Г приведена в табл. 10.1.
В первой строке указывается остаток составов, переходящий с предыдущих суток на начало первого расчетного интервала. Во второй графе против соответствующих расчетных интервалов делаются пометки, что в течение этих интервалов горка не может быть использована для роспуска, например, по причинам смены бригад, техосмотра и ремонта горочных устройств, формирования поездов на горке.
В графе 3 из графика исполненной работы проставляется число поездов, прибывших в расформирование за каждый расчетный интервал. Графы 4 и 5 заполняются в процессе выполнения расчетов путем решения уравнения баланса.
Таблица 10.1. Расчет простоя составов в ПП
| Номер | Техно- | Число | Число | Остаток |
| расчетного | логи- | соста- | соста- | составов |
| интервала | ческие | вов, | вов | на конец |
| по- | при- | для | расчетного | |
| метки | быв- | расфор- | интервала | |
| ших | мирова- | в том чис- | ||
| за | ния | ле готовых | ||
| расчет- | (в том | к роспуску роспуску) | ||
| ный | числе | |||
| интер- | готовых | |||
| вал | кроспуску) | |||
| 6(3) | ||||
| – | 6(3) | 5(2) | ||
| – | 7(3) | 6(2) | ||
| … | – …. | …. | 7(3) …. | 6(2) …. |
| 7(4) | 5(3) | |||
| Итого за | ||||
| сутки |
Поскольку за каждый расчетный интервал с горки распускается один состав, в графе 5 проставляется значение, на единицу меньшее, чем в графе 4, кроме случаев, когда в графе 2 стоит особая отметка, означающая, что в данном интервале роспуск невозможен.
Средний простой составов в парке определяется:
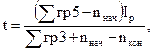 |
где ∑гр5 – итог числителей графы 5; ∑грЗ – число составов, прошедших через парк за сутки, без учета угловых и местных передач; Iр – расчетный интервал вывода составов из парка, мин; nнач, кон –соответственно переходящие остатки составов на начало и конец суток.
Для примера (см. табл. 10.1)
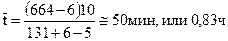 |
Аналогично выполняется расчет для других подсистем, затем результаты суммируются и получается общий простой для станции (сортировочной системы).
Трудоемкость расчетов (с помощью табличного моделирования) сокращена по сравнению с графической моделью при той же трудоемкости подготовки исходных данных, однако точность расчета показателей по табличному моделированию ниже: не учитывается занятость путей, работа локомотивов, враждебность в горловинах и др. Кроме того, нарушаются требования системного подхода – каждая подсистема рассматривается в качестве независимо функционирующей обслуживающей системы. Поэтому достоверность результатов, полученных табличным моделированием, часто оказывается невысокой.
Можно выделить два направления создания аналитических методов расчета простоя вагонов на станциях. Первое – на основе использования математического аппарата теории массового обслуживания (ТМО) и второе – с использованием аналитическо-статистических зависимостей. Во всех случаях аналитические зависимости используются для определения среднего времени нахождения вагона в каждой подсистеме. В связи со сложностью технологических линий и значительным числом фаз обслуживания аналитические методы также не учитывают влияние подсистем друг на друга.
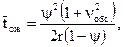 Для расчетов показателей станций проф. Н. Н. Шабалин предложил определять время ожидания обслуживания (обработки, расформирования, формирования и т. д.) на основе ТМО по формуле
Для расчетов показателей станций проф. Н. Н. Шабалин предложил определять время ожидания обслуживания (обработки, расформирования, формирования и т. д.) на основе ТМО по формуле
где Ψ – коэффициент загрузки выходного канала; 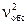 – коэффициент вариации времени обслуживания; r – среднечасовая интенсивность поступления поездов (составов).
– коэффициент вариации времени обслуживания; r – среднечасовая интенсивность поступления поездов (составов).
Эта формула получена исходя из предположения, что входящий транспортный поток является простейшим.
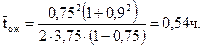 Пример. Требуется определить простой составов в ожидании расформирования, если r = 3,75 поездо-ч, Ψ = 0,75,
Пример. Требуется определить простой составов в ожидании расформирования, если r = 3,75 поездо-ч, Ψ = 0,75, 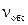 = 0,9:
= 0,9:
Использование предложенной проф. Н. Н. Шабалиным методики для практических целей показало, что приемлемые результаты получаются при уровнях загрузки выходного канала до 0,65-0,7. При больших значениях Ψ результаты расчетов отклоняются от реальных в сторону увеличения, превосходя фактические в несколько раз.
Аналогичные методики разработаны профессорами А. М. Акулиничевым, А. В. Быкодоровым, И. Б. Сотниковым на основе распределения интервалов входящего потока по закону Эрланга. Так, например, проф. А. М. Акулиничев среднее время ожидания обслуживания в подсистеме станции определяет:
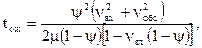 |
где 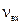 – коэффициент вариации входящего потока; μ – интенсивность обслуживания, поездов/ч.
– коэффициент вариации входящего потока; μ – интенсивность обслуживания, поездов/ч.
Пример. Для исходных данных предыдущего примера рассчитать простои в ожидании, если коэффициент вариации входного потока 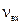 =0,8:
=0,8:
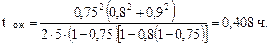 |
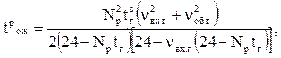 Если конкретизировать формулу для расчета времени ожидания расформирования, получится следующая зависимость:
Если конкретизировать формулу для расчета времени ожидания расформирования, получится следующая зависимость:
где Np – суточное число поездов, прибывающих в расформирование; tг – горочный технологический интервал, ч.
По методике проф. И. Б. Сотникова средняя длина очереди в ожидании обслуживания при относительно невысоких уровнях загрузки ( Ψ≤ 0,7) определяется
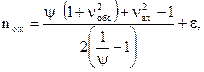 |
(10.5)
где ε – погрешность, принимаемая на основе статистических исследований. При 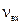 = 1 ε = 0; при
= 1 ε = 0; при 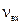 = 0,9 ε = 0,03; при
= 0,9 ε = 0,03; при 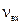 = 0,8 ε = 0,06; при
= 0,8 ε = 0,06; при 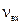 = 0,7 ε = 0,08.
= 0,7 ε = 0,08.
Для высоких уровней загрузки системы (Ψ≥0,82 ) средняя длина очереди
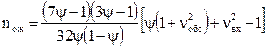 |
(10.6)
Для промежуточных уровней (0,7 < Ψ< 0,82) среднюю длину очереди рекомендуется определять интерполированием.
Среднее время ожидания обслуживания можно определить по формуле tож = nож / r.
Пример. Для исходных данных предыдущих примеров найти простой в ожидании расформирования.
Поскольку 0,7 < Ψ < 0,82, расчеты производим дважды, по формулам (10.5) и (10.6):
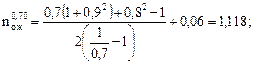 | |||
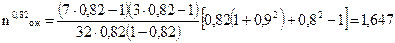 |
Путем интерполяции находим, что при Ψ = 0,75 nож=1,338. Тогда tож= 1,338/3,75 = 0,357 ч.
Во всех перечисленных выше методиках принципы определения простоя вагонов едины. Вначале определяется продолжительность технологических операций, затем –межоперационные простои перед каждой операцией и далее суммируются все полученные значения. Так, для подсистемы ВхУ-ПП-Г определяются продолжительность обслуживания в ПП и среднее время ожидания, затем среднее время нахождения вагона под расформированием и среднее время его ожидания. При этом необходимо для второй фазы обслуживания знать новые значения коэффициента вариации, поскольку при обслуживании в парке происходит трансформация потока и его показатели неравномерности изменяются.
Таким образом, использование закономерностей ТМО для определения простоя вагонов на станциях предполагает наличие коэффициентов вариации входного потока и времени обслуживания. Их значения можно получить в настоящее время лишь статистическим путем. Это не всегда возможно и поэтому значения этих коэффициентов принимают приближенно на основе статистических выборок. Кроме того, точность 

 результатов зависит от уровней загрузки выходного канала. При больших загрузках результаты расчета простоя вагонов оказываются выше фактически реализуемых в подсистеме, причем чем ближе значения коэффициента загрузки к единице, тем значительнее расхождения.
результатов зависит от уровней загрузки выходного канала. При больших загрузках результаты расчета простоя вагонов оказываются выше фактически реализуемых в подсистеме, причем чем ближе значения коэффициента загрузки к единице, тем значительнее расхождения.
Поэтому широко распространенными методами расчета простоя вагонов остаются методы, основанные на аналитическо-статистических зависимостях, в которых необходимые параметры установлены на основе обработки статистических данных.
Дата добавления: 2016-06-02; просмотров: 1993;
