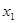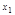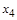Дизъюнктивные нормальные формы
Элементарным произведением называется конъюнкт, в который любая переменная входит не более одного раза. Например, формула  - элементарное произведение, а формула
- элементарное произведение, а формула 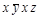 элементарным произведением не является.
элементарным произведением не является.
Формула 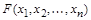 называется импликантой формулы
называется импликантой формулы 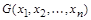 , если
, если  - элементарное произведение и
- элементарное произведение и 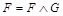 , т.е. для функций
, т.е. для функций 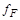 и
и 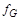 , соответствующих формулам
, соответствующих формулам  и
и 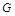 , справедливо неравенство
, справедливо неравенство 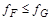 при любом наборе переменных
при любом наборе переменных 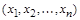 . Формула
. Формула 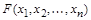 называется импликантой функции
называется импликантой функции 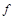 , если
, если  - импликанта совершенной ДНФ, представляющей функцию
- импликанта совершенной ДНФ, представляющей функцию 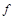 . Импликанта
. Импликанта 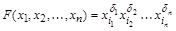 формулы
формулы 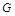 называется простой, если после отбрасывания любой литеры из
называется простой, если после отбрасывания любой литеры из  не получается формула, являющаяся импликантой формулы
не получается формула, являющаяся импликантой формулы 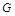 .
.
Пример 14: Найти все импликанты и простые импликанты для формулы  .
.
Решение: Составим таблицу
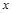
| 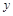
| 
| 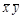
| 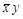
| 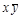
| 
| 
| 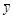
| 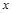
| 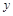
|
Итак, существуют 8 элементарных произведений с переменными 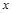 и
и 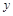 (эти произведения перечислены в названиях 4 – 11 столбцов таблицы). Из таблицы следует, что формулы
(эти произведения перечислены в названиях 4 – 11 столбцов таблицы). Из таблицы следует, что формулы 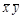 ,
, 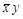 ,
,  ,
,  ,
, 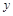 являются импликантами формулы
являются импликантами формулы  (т.к. значения 4-го, 5-го, 7-го, 8-го и 11-го столбцов таблицы не превосходят значений 3-го столбца). Из перечисленных импликант простыми являются формулы
(т.к. значения 4-го, 5-го, 7-го, 8-го и 11-го столбцов таблицы не превосходят значений 3-го столбца). Из перечисленных импликант простыми являются формулы  и
и 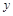 (формула
(формула 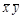 , например, не является простой импликантой, поскольку, отбрасывая литеру
, например, не является простой импликантой, поскольку, отбрасывая литеру 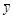 , получаем импликанту
, получаем импликанту  ).
).
Пример 15: Аналогичным приемом можно показать (выполнить самостоятельно), что для формулы 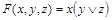 конъюнкции
конъюнкции 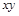 и
и 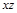 являются простыми импликантами, а
являются простыми импликантами, а 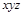 - импликанта, но не простая.
- импликанта, но не простая.
Дизъюнкция всех простых импликант данной формулы (функции) называется сокращенной ДНФ.
Функция, соответствующая формуле  (см. пример 14), предста-вима формулой
(см. пример 14), предста-вима формулой 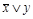 , которая является ее сокращенной ДНФ.
, которая является ее сокращенной ДНФ.
Любая булева функция, не являющаяся константой 0, представима в виде сокращенной ДНФ.
Сокращенная ДНФ может содержать так называемые лишние импли-канты, удаление которых не меняет таблицы истинности. Если из сокращенной ДНФ удалить все лишние импликанты, то получается ДНФ, называемая тупиковой. Различные тупиковые ДНФ одной и той же функции могут содер-жать разное число вхождений переменных. Выбор среди всех тупиковых ДНФ данной функции формы с наименьшим числом вхождений переменных дает минимальную дизъюнктивную нормальную форму (МДНФ). Отметим, что в общем случае у одной функции может быть несколько различных МДНФ, но все они имеют одинаковое число переменных, причем наименьшее среди всех ДНФ данной функции.
Рассмотрим два метода минимизации логических функций: метод Квайна и метод карт Карно.
Метод Квайна
Сформулируем и докажем следующие три операции.
1) Операция полного склеивания: 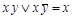 .
.
Доказательство: 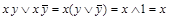 .
.
2) Операции неполного склеивания: 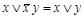 ;
;  .
.
Доказательство: 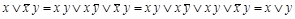 ;
;
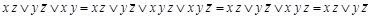 .
.
3) Операции элементарного поглощения: 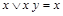 ;
; 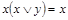 .
.
Доказательство: 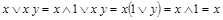 ;
;
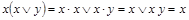 .
.
Примечание: В данных операциях вместо 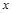 и/или
и/или 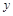 могут участвовать более сложные формулы (или функции). Например, если в равенстве
могут участвовать более сложные формулы (или функции). Например, если в равенстве 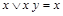 вместо
вместо 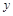 использовать
использовать 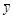 , то получим тот же результат:
, то получим тот же результат: 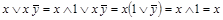 .
.
Теорема Квайна: Если исходя из совершенной ДНФ функции произвести все возможные операции неполного склеивания, а затем элементарного поглощения, то в результате получится сокращенная ДНФ, т. е. дизъюнкция всех простых импликант.
Метод Квайна продемонстрируем на следующем примере.
Пример 16: Пусть функция 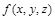 задана совершенной ДНФ:
задана совершенной ДНФ:
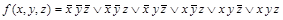 .
.
Тогда, производя в два этапа все возможные операции неполного склеивания, а затем элементарного поглощения, имеем
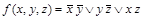 .
.
В последней формуле смежных пар переменных нет, поэтому получена сокращенная ДНФ.
Для перехода к тупиковым ДНФ и выбора среди них минимальной построим таблицу Квайна. В строки этой таблицы записываются простые импликанты, а в столбцы – конституенты единицы. Если импликанта является частью конституенты, то на пересечении соответствующих строки и столбца ставится знак (чаще всего "1" или "х").
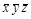
| 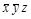
| 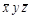
| 
| 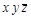
| 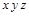
| |
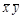
| ||||||
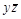
| ||||||
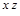
|
Для выделения тупиковых ДНФ рекомендуется следующая последо-вательность шагов:
1) Выделяются все обязательные импликанты, которые имеют единственную пометку в каком-либо столбце. Они не могут быть удалены и входят в тупиковую ДНФ.
2) Среди оставшихся импликант условно вычеркивается строка вместе с соответствующими пометками. Если после вычеркивания в каждом столбце таблицы остается хотя бы по одной отметке, то проверяемая импликанта является лишней.
Может получиться несколько вариантов тупиковых ДНФ. Минимальная ДНФ выбирается по наименьшему значению суммарного числа переменных в ней.
В последнем примере сокращенная ДНФ совпала с единственной тупиковой (т. к. в каждом столбце таблицы Квайна стоит только одна отметка), и поэтому она является минимальной:
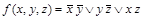 .
.
Метод карт Карно
При небольшом числе переменных используют графическое пред-ставление логических функций в виде карт Карно. Карта состоит из 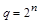 клеток, причем каждой из клеток соответствует один из
клеток, причем каждой из клеток соответствует один из  наборов переменных. Например, для двух переменных (
наборов переменных. Например, для двух переменных (  ) имеем
) имеем 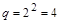 клетки. Значение переменной обычно задается в виде черты по периметру карты: если черта есть – переменная в пределах строки или столбца равна 1; если черты нет – переменная равна 0.
клетки. Значение переменной обычно задается в виде черты по периметру карты: если черта есть – переменная в пределах строки или столбца равна 1; если черты нет – переменная равна 0.
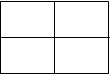
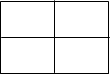
Варианты карт Карно для двух, трех и четырех переменных представ-лены, соответственно, на рисунках 1 – 3.
При 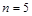 карта имеет 32 клетки, при
карта имеет 32 клетки, при  – 64 клетки. Приведенное на рис. 1 – 3 расположение переменных по строкам или столбцам не является единственным. Обязательное требование состоит в том, что при переходе из клетки в клетку по вертикали или горизонтали происходит инверсия (изменение логического значения) только одной переменной.
– 64 клетки. Приведенное на рис. 1 – 3 расположение переменных по строкам или столбцам не является единственным. Обязательное требование состоит в том, что при переходе из клетки в клетку по вертикали или горизонтали происходит инверсия (изменение логического значения) только одной переменной.
 |

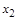
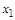 0 1
0 1 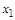
 | |||
 |
0 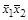
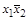 0 0 1 0
0 0 1 0
 или
или
1 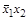
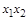
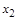 0 1 1 1
0 1 1 1
Рис. 1. Варианты карт Карно для двух переменных
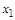
 |
 0 0 0 0 0 0
| 0 1 0 | 1 1 0 | 1 0 0 | ||
0 0 1 | 0 1 1 | 1 1 1 | 1 0 1 |

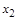
Рис. 2. Вариант карты Карно для трех переменных
| |||
| |||
|


|




|




 0 0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 0 4 12 8
0 0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 0 4 12 8

|


|

 0 0 0 1 0 1 0 1 1 1 0 1 1 0 0 1 1 5 13 9
0 0 0 1 0 1 0 1 1 1 0 1 1 0 0 1 1 5 13 9

 0 0 1 1 0 1 1 1 1 1 1 1 1 0 1 1 3 7 15 11
0 0 1 1 0 1 1 1 1 1 1 1 1 0 1 1 3 7 15 11

 0 0 1 0 0 1 1 0 1 1 1 1 1 0 1 0 2 6 14 10
0 0 1 0 0 1 1 0 1 1 1 1 1 0 1 0 2 6 14 10


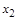
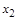
Рис. 3. Варианты карт Карно для четырех переменных
Пример 17: Карта Карно для функции 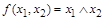 показана на рис. 4.
показана на рис. 4.
Пример 18: Карта Карно для функции 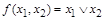 показана на рис. 5.
показана на рис. 5.
Пример 19: Карта Карно для функции
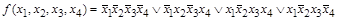
показана на рис.6.
Метод карт Карно целесообразно использовать при минимизации логических функций не более 6 переменных. В данном методе заданную логическую функцию приводят к СДНФ и заполняют карту Карно. Наличие единиц в соседних по вертикали или горизонтали клетках карты соответствует смежным наборам переменных, которые могут быть склеены. Для этого в карте Карно единичные наборы функции обводят контурами по специальным, ниже описанным, правилам.


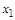
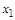
 | |||
 |
0 0

 или
или
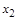 0 1
0 1 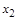 1
1
Рис. 4. Карта Карно для конъюнкции двух переменных


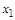
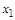
 | |||
 |
0 1 1

 или
или
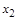 1 1
1 1 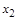 1 1
1 1
Рис. 5. Карта Карно для дизъюнкции двух переменных
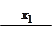

| |||||

| |||||

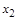
Рис. 6. Карта Карно для функции примера 19
Правила реализации метода карт Карно:
1) Контуром обводятся только клетки, содержащие единицы.
2) Склеиванию подлежит только число клеток, равное 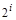 ;
; 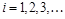 .
.
3) Единицы в крайних клетках одного столбца или строки могут склеиваться
(рис. 7).
4) Каждый контур должен содержать как можно большее число клеток с единицами.
5) Нельзя проводить контур внутри контура, т. е. каждая клетка может входить в несколько контуров, но каждый контур должен иметь, как минимум, одну клетку, принадлежащую только ему.
6) Объединением контуров, содержащих максимально возможное число клеток, получается минимальная ДНФ в виде дизъюнкции переменных, которые в пределах одного обведенного контура не меняют своего значения.
7) Если возникает возможность проведения контуров различными вариантами, то это говорит о наличии нескольких тупиковых ДНФ.

| 
| ||

| |||

Рис. 7. Карта Карно с вариантами склеивания крайних клеток
столбца или строки
Пример 20: Пусть логическая функция задана своей СДНФ
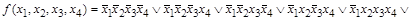
 .
.
Построим карту Карно (рис. 8).



|
 |
 0000 0000
| |||||
 1 1
|
 1 1
| ||||

| |||||

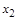
Рис. 8. Карта Карно для функции примера 20
В соответствии с правилами реализации на этой карте обведены контуры, пронумерованные римскими цифрами: I , II , III, IV . Каждому контуру соответствует конъюнкция переменных в искомой МДНФ.
Правило составления таких конъюнкций поясняет следующая таблица.
| Номер контура | I | II | III | IV |
| Наборы переменных в этом контуре | ||||
| Конъюнкция в минимальной ДНФ | 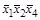
| 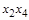
| 
| 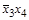
|
Итак, если переменная  в наборах какого-либо контура имеет постоянное значение 1, то она входит в соответствующую конъюнкцию в виде
в наборах какого-либо контура имеет постоянное значение 1, то она входит в соответствующую конъюнкцию в виде  ; если эта переменная принимает значение 0, то она входит в соответ-ствующую конъюнкцию в виде
; если эта переменная принимает значение 0, то она входит в соответ-ствующую конъюнкцию в виде 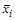 (переменные с изменяющимися в наборах контура значениями в соответствующей конъюнкции не участвуют).
(переменные с изменяющимися в наборах контура значениями в соответствующей конъюнкции не участвуют).
По последней таблице (или по карте Карно (рис. 8)) можно записать искомую МДНФ:
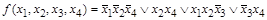 .
.
Обратим внимание, что невыполнение условия построения контуров с максимально возможным числом клеток приведет к построению тупиковой (не обязательно минимальной) ДНФ.
Следующим примером покажем случай наличия нескольких тупиковых (и одновременно минимальных) ДНФ.
Пример 21: Рассмотрим карту Карно (рис. 9).
|


 IV I II
IV I II
 | |||
 | |||
| |||||||
 
 0001 0001
|  1 1
|
 1 1
| |||||
|
 0011 0011
| |||||||

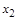
Рис. 9. Карта Карно для примера 21
По обведенным пяти контурам (рис. 9) можно составить две тупиковые ДНФ:
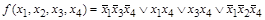 ,
,
 I II III IV номера контуров
I II III IV номера контуров
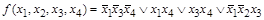 ,
,
 I II III V номера контуров
I II III V номера контуров
Под каждой формулой указаны номера контуров, соответствующих данным (расположенным выше номеров) конъюнкциям.
Обе тупиковые ДНФ содержат по одинаковому числу вхождений переменных, следовательно, любая из них может быть принята в качестве минимальной.
Дата добавления: 2016-05-25; просмотров: 3327;