Совершенные нормальные формы
Пусть 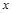 – логическая переменная,
– логическая переменная, 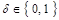 . Введем обозначение
. Введем обозначение 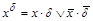 . Выражение
. Выражение
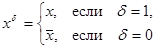
называется литерой. Литеры 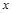 и
и  называются контрарными.
называются контрарными.
Отметим, что 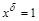 тогда и только тогда, когда
тогда и только тогда, когда  .
.
Теорема (о разложении функций по переменным): Каждую функцию алгебры логики 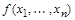 при любом
при любом 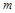
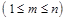 можно представить в следующей форме:
можно представить в следующей форме:
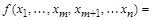
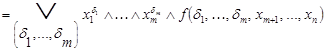 ,
,
где дизъюнкция берется по всем возможным наборам 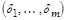 .
.
Это представление называется разложением функции по 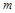 переменным.
переменным.
Следствие 1: Разложение функции по одной переменной, например 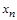 имеет вид:
имеет вид:
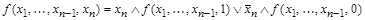 .
.
Следствие 2: Разложение функции по 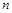 переменным имеет вид:
переменным имеет вид:
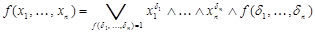 .
.
Элементарной конъюнкцией, или конъюнктом называется конъюнкция литер. Элементарной дизъюнкцией, или дизъюнктом называется дизъюнкция литер.
Например, формулы 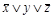 и
и 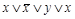 – дизъюнкты, формулы
– дизъюнкты, формулы 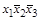 и
и 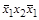 – конъюнкты,
– конъюнкты,  является одновременно и дизъюнктом, и конъюнктом, а формула
является одновременно и дизъюнктом, и конъюнктом, а формула 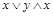 не является ни элементарной дизъюнкцией, ни элементарной конъюнкцией.
не является ни элементарной дизъюнкцией, ни элементарной конъюнкцией.
Дизъюнкция конъюнктов называется дизъюнктивной нормальной формой (ДНФ); конъюнкция дизъюнктов называется конъюнктивной нормальной формой (КНФ).
Например, формула 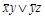 – ДНФ, формула
– ДНФ, формула 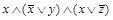 – КНФ, а формула
– КНФ, а формула 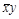 является одновременно КНФ и ДНФ.
является одновременно КНФ и ДНФ.
Теорема: 1) Любая формула эквивалентна некоторой ДНФ. 2) Любая формула эквивалентна некоторой КНФ.
Опишем алгоритм приведения формулы к ДНФ (КНФ).
1. Выразить все логические операции, участвующие в построении формулы, через дизъюнкции, конъюнкции и отрицания, используя эквивалентности и определения операций 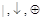 .
.
2. Используя законы де Моргана, перенести все отрицания к переменным и сократить двойные отрицания по правилу 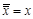 .
.
3. Используя закон дистрибутивности, преобразовать формулу так, чтобы все конъюнкции (дизъюнкций) выполнялись раньше дизъюнкций (конъюнкций).
В результате применения пп. 1 – 3 получается ДНФ (КНФ) данной формулы.
Например, для формулы 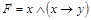 имеем:
имеем: 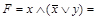
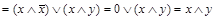 , то есть получено две ДНФ:
, то есть получено две ДНФ:
ДНФ 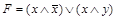 ; ДНФ
; ДНФ 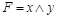 .
.
Для формулы 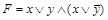 можно получить (выполнить самостоятельно): КНФ
можно получить (выполнить самостоятельно): КНФ 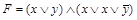 , КНФ
, КНФ 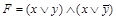 .
.
Любая булева функция может иметь бесконечно много представлений в виде ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).
Пусть 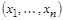 – набор логических переменных,
– набор логических переменных, 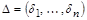 – набор нулей и единиц. Конституентой единицы набора
– набор нулей и единиц. Конституентой единицы набора 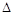 называется конъюнкт
называется конъюнкт 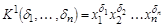 . Конституентой нуля набора
. Конституентой нуля набора 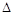 называется дизъюнкт
называется дизъюнкт  . Отметим, что
. Отметим, что  (или
(или 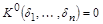 ) тогда и только тогда, когда
) тогда и только тогда, когда 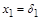 ,
,  , … ,
, … ,  .
.
Совершенной ДНФ называется дизъюнкция некоторых конституент единицы, среди которых нет одинаковых, а совершенной КНФ называется конъюнкция некоторых конституент нуля, среди которых нет одинаковых. Итак, СДНФ (СКНФ) есть ДНФ (КНФ), в которой в каждый конъюнкт (дизъюнкт) каждая переменная  из набора
из набора 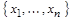 входит ровно один раз, причем входит либо сама
входит ровно один раз, причем входит либо сама  , либо ее отрицание
, либо ее отрицание 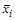 .
.
Например, формула 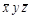 есть конституента единицы
есть конституента единицы 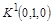 , формула
, формула 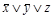 есть конституента нуля
есть конституента нуля 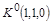 , формула
, формула 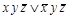 – СДНФ, формула
– СДНФ, формула 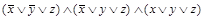 – СКНФ, а формула
– СКНФ, а формула  не является СДНФ.
не является СДНФ.
СДНФ называется совершенной, потому что каждое слагаемое в дизъюнкции включает все переменные; дизъюнктивной, потому что главная операция – дизъюнкция, а почему она называется нормальной, объясняется следующими соображениями. Говорят, что некоторый класс формул 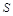 имеет нормальную форму, если существует другой класс формул
имеет нормальную форму, если существует другой класс формул  , которые называются нормальными формами, такой, что любая формула класса
, которые называются нормальными формами, такой, что любая формула класса 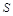 имеет единственную равносильную формулу из класса
имеет единственную равносильную формулу из класса  . Наличие у класса формул нормальной формы обеспечивает разрешимость, то есть наличие алгоритма проверки равносильности. Один и тот же класс
. Наличие у класса формул нормальной формы обеспечивает разрешимость, то есть наличие алгоритма проверки равносильности. Один и тот же класс 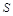 может иметь несколько различных нормальных форм, то есть несколько различных классов
может иметь несколько различных нормальных форм, то есть несколько различных классов  .
.
Теорема (о функциональной полноте): Для любой булевой функции 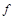 найдется формула
найдется формула  , представляющая функцию
, представляющая функцию 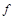 . Если
. Если 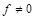 , то существует представляющая ее формула, находящаяся в СДНФ:
, то существует представляющая ее формула, находящаяся в СДНФ:
 ,
,
и такое представление единственно с точностью до порядка следования конституент единицы. Если 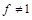 , то существует представляющая ее формула, находящаяся в СКНФ:
, то существует представляющая ее формула, находящаяся в СКНФ:
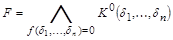 ,
,
и такое представление единственно с точностью до порядка следования конституент нуля.
Константа 0 может быть представлена только СКНФ (  ), а константа 1 – только СДНФ (
), а константа 1 – только СДНФ ( 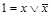 ).
).
Пример 9: Для булевой функции 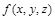 даны наборы переменных, на которых функция принимает нулевое значение:
даны наборы переменных, на которых функция принимает нулевое значение: 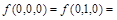
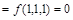 . Остальные значения функции равны единице. Найти СДНФ и СКНФ.
. Остальные значения функции равны единице. Найти СДНФ и СКНФ.
Решение: Строим следующую таблицу.
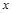
| 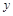
| 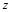
| 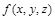
| Конституенты единицы | Конституенты нуля |
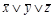
| |||||
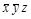
| |||||
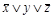
| |||||
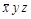
| |||||
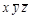
| |||||

| |||||
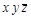
| |||||
|
По пятому столбцу таблицы формируем:
СДНФ 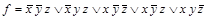 ,
,
а по шестому столбцу формируем:
СКНФ 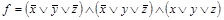 .
.
Описанный в примере 9 способ нахождения СДНФ и СКНФ по таблице истинности бывает часто более трудоемким, чем следующий алгоритм.
Для нахождения СДНФ данную формулу привести сначала к ДНФ, а затем преобразовать ее конъюнкты в конституенты единицы с помощью следующих действий:
1) если в конъюнкт входит некоторая переменная вместе со своим отрицанием, то удалить этот конъюнкт из ДНФ;
2) если в конъюнкт одна и та же литера 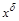 входит несколько раз, то удалить все литеры
входит несколько раз, то удалить все литеры 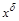 , кроме одной;
, кроме одной;
3) если в некоторый конъюнкт 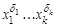 не входит переменная
не входит переменная 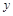 , то этот конъюнкт заменить на эквивалентную формулу
, то этот конъюнкт заменить на эквивалентную формулу 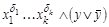 и, применяя закон дистрибутивности, привести полученную формулу к ДНФ; если недостающих переменных несколько, то для каждой из них к конъюнкту добавить соответствующую формулу вида
и, применяя закон дистрибутивности, привести полученную формулу к ДНФ; если недостающих переменных несколько, то для каждой из них к конъюнкту добавить соответствующую формулу вида 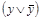 ;
;
4) если в полученной ДНФ имеется несколько одинаковых конституент единицы, то оставить только одну из них. В результате получается СДНФ.
Алгоритм приведения КНФ к СКНФ аналогичен описанному выше алгоритму приведения ДНФ к СДНФ (составить самостоятельно).
Пример 10: Найти СДНФ для формулы: 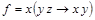 .
.
Решение: 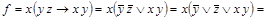
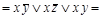 ДНФ
ДНФ 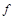 .
.
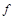 = ДНФ
= ДНФ 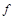 =
= 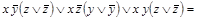
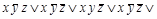
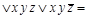
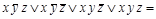 СДНФ
СДНФ 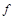 .
.
Ответ: СДНФ 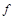 =
= 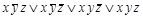 .
.
Пример 11: Для формулы из примера 10 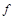
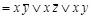 найти ее СКНФ, предварительно приведя ее к КНФ.
найти ее СКНФ, предварительно приведя ее к КНФ.
Решение:  =КНФ
=КНФ 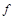 .
.
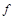 =КНФ
=КНФ 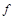 =
= 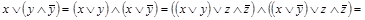
 СКНФ
СКНФ 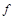 .
.
Ответ: СКНФ 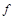
 .
.
Пример 12: Для формулы из примера 10 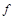
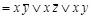 найти СКНФ, записав предварительно СДНФ ее отрицания, а затем применив принцип двойственности.
найти СКНФ, записав предварительно СДНФ ее отрицания, а затем применив принцип двойственности.
Решение: СДНФ 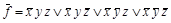 .
.
СКНФ 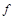 =
= 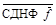
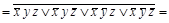
 .
.
Дата добавления: 2016-05-25; просмотров: 1696;
