Дайте определение базисного и балансирующего узла при расчете установившегося режима электроэнергетической системы.

Из теоретической электротехники известно, что для схемы,

содержащей N узлов, количество независимых уравнений, составленных

по первому закону Кирхгофа, составляет N–1. Следовательно, для одного

любого узла схемы не требуется запись уравнения по первому закону

Кирхгофа. Такой узел называется балансирующим по току (мощности). В

качестве балансирующего узла может быть принят любой узел. В

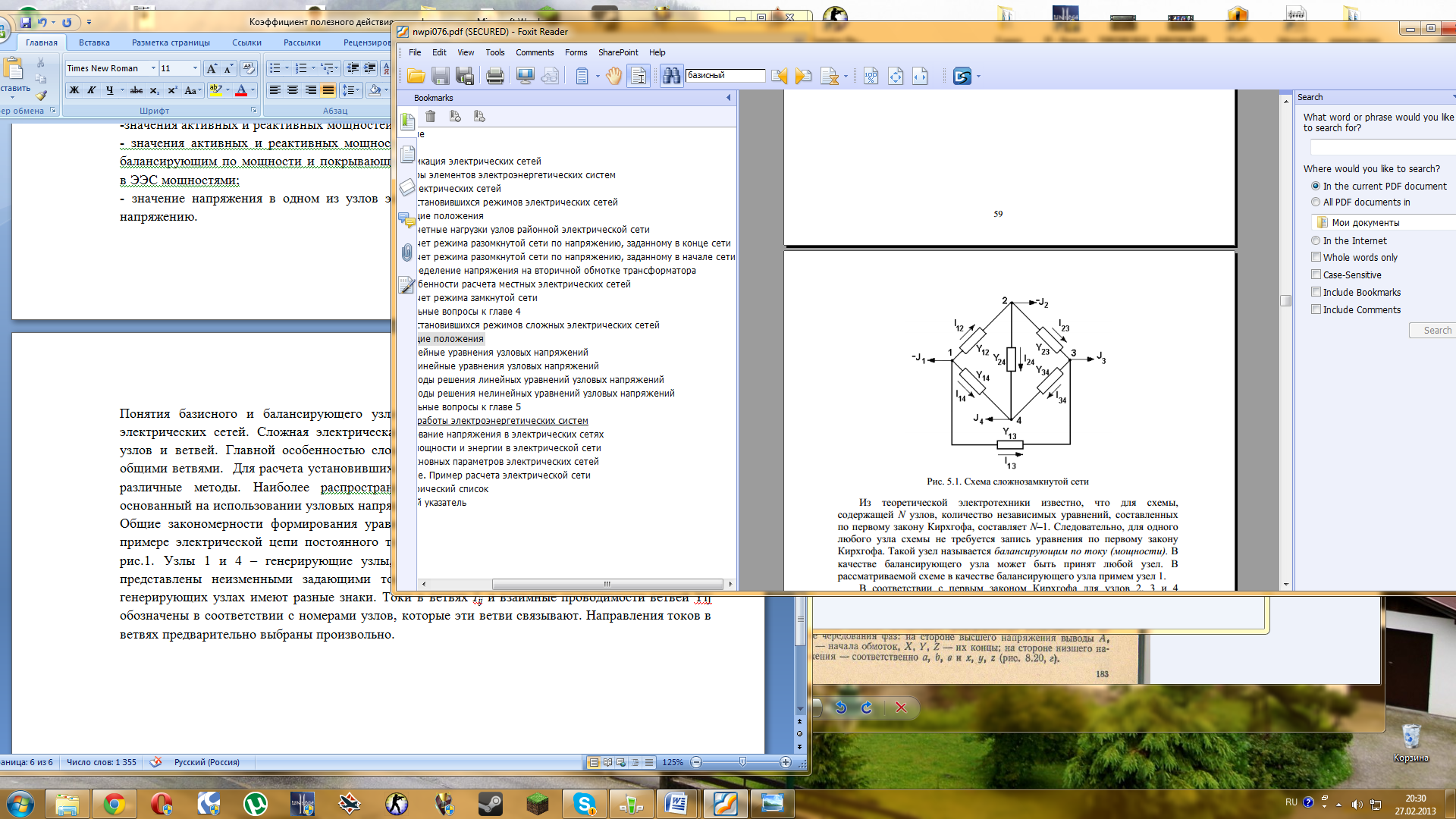
рассматриваемой схеме в качестве балансирующего узла примем узел 1.

В соответствии с первым законом Кирхгофа для узлов 2, 3 и 4

запишем уравнения

12–I23–I24=-J2I;

13+I23-I34=J3;I (5.1)

14+I24+I34=J4I.

В соответствии с законом Ома ток в ветви между двумя любыми

узлами i и j равен

ij=(Ui–Uj)Yij,I (5.2)

где Yij – взаимная проводимость ветви между узлами i и j.

После подстановки (5.2) в (5.1) и алгебраических преобразований

получим уравнения узловых напряжений для 4-узловой сети постоянного

тока

12U1+Y(–Y21–Y23–Y24)U2+Y32U3+Y42U4=–J2;

Y13U1+Y23U2+(–Y31–Y32–Y34)U3+Y43U4=J3; (5.3)

Y14U1+Y24U2+Y34U3+(–Y41–Y42–Y43)U4=J4.

Система с (N–1) уравнениями содержит N искомых напряжений в

узлах и, следовательно, имеет бесконечное количество решений. Для

однозначного определения напряжений в узлах сети необходимо задаться

величиной напряжения в одном из узлов. Такой узел называется базисным

по напряжению. В качестве базисного узла может быть принят любой

узел, однако с целью упрощения вычислительной процедуры

целесообразно базисный узел совместить с балансирующим. Поэтому в

качестве базисного узла примем узел 1. Заданное напряжение в этом узле

обозначим Uб.

Поскольку напряжение U1 является заданным, перенесем

составляющие Y12U1, Y13U1 и Y14U1 в правые части уравнений и примем для

базисного и балансирующего узла 1 индекс «б». В результате получим

систему

–Y21– (Y23–Y24)U2+Y23U3+Y24U4=–J2–Y2бUб;

Y32U2+(–Y31–Y32–Y34)U3+Y34U4=J3–Y3бUб; (5.4)

Y42U2+Y43U3+(–Y41–Y42–Y43)U4=J4-Y4бUб.

Введем следующие обозначения:

22=–Y21–Y23Y–Y24;

33=–Y31–Y32Y–Y34; (5.5)

44=–Y41–Y42Y–Y43.

Назовем Y22, Y33 и Y44 собственными проводимостями узлов 2, 3 и 4.

Собственная проводимость узла i равна сумме взятых с

противоположным знаком взаимных проводимостей ветвей, сходящихся в

узле i.

С учетом обозначений (5.5) уравнения узловых напряжений (5.4)

запишем в более компактном виде:

22U2+Y23YU3+Y24U4=–J1–Y2бUб;

32U2+Y33YU3+Y34U4=J3–Y3бUб; (5.6)

42U2+Y43YU3+Y44U4=J4–Y4бUб.

Из (5.6) видно, что для сети постоянного тока при представлении

активных элементов сети неизменными токами система уравнений

узловых напряжений является линейной системой алгебраических

уравнений.