Остальные задачи для практических занятиях по данной теме будут предлагаться преподавателем.
Эйлеровы циклы
3.1.1.1 Начало теории графов, как раздела математики, связывают с так называемой задачей о кёнигсбергских мостах. Эта знаменитая в своё время задача состоит в следующем. Семь мостов города Кёнигсберга (ныне г.Калининград) были расположены на реке Прéгель согласно рисунку 3.1. Спрашивается, можно ли, выйдя из дома, вернуться обратно, пройдя в точности один раз по каждому мосту?
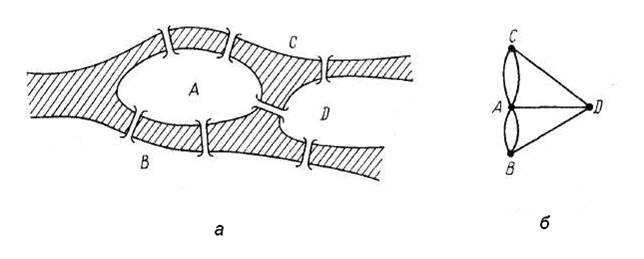
Рисунок 3.1 – Задача о кёнигсбергских мостах
Эйлер представил город в виде графа (точнее, мультиграфа) G, вершинами которого являются его участки суши А, В, С и D, а рёбрами – мосты (см. рисунок 3.1,б). Обходу мостов соответствует последовательность рёбер графа задачи, в которой два соседних ребра имеют общую вершину, т.е. маршрут. Таким образом, задачу о кёнигсбергских мостах можно на языке теории графов сформулировать так: есть ли в мультиграфе G цикл, содержащий все рёбра этого мультиграфа?
Эйлер доказал неразрешимость задачи о кёнигсбергских мостах и решил следующую общую проблему теории графов: при каких условиях связный граф содержит цикл, проходящий через каждое его ребро?
Цикл в графе называется эйлеровым, если он содержит все рёбра графа. Связный граф, в котором есть эйлеров цикл, называется эйлеровым графом. Такой граф можно нарисовать, не отрывая карандаша от бумаги и не повторяя линий.
Теорема (Л.Эйлер, 1736г.). Связный конечный неориентированный граф G является эйлеровым тогда и только тогда, когда степени всех его вершин чётны.
В графе задачи о кёнигсбергских мостах (см. рисунок 3.1,б) все вершины имеют нечётную степень, следовательно, её решение невозможно. А, например, граф на рисунке 3.2, а является эйлеровым, поскольку он содержит эйлеров цикл (1, 2, 3, 4, 5, 6, 4, 2, 6, 1). В этом графе есть и другие эйлеровы циклы, причём любые два таких цикла отличаются друг от друга только порядком обхода рёбер.

а б
Рисунок 3.2 – Примеры эйлеровых графов
Помимо задачи о кёнигсбергских мостах известен ряд других старинных занимательных задач (головоломок), решение которых сводится к выяснению вопроса «является ли граф эйлеровым?». В одной из них требуется обрисовать фигуру, именуемую саблями (знаком) Магомета (см. рисунок 3.2, б), не отрывая карандаша от бумаги и не повторяя линий.
Таким образом, эйлеровы графы – это такие графы, которые можно изобразить одним рóсчерком пера, причём процесс рисования начинается и заканчивается в одной и той же точке.
3.1.1.2 Естественно возникает вопрос: как найти хотя бы одинэйлеров цикл в эйлеровом графе G, т.е. как занумеровать рёбра графа числами 1, 2,..., /EG/ с тем, чтобы номер, присвоенный ребру, указывал, каким по счёту это ребро проходится в эйлеровом цикле? Это можно сделать, придерживаясь следующих двух правил:
а) начиная с произвольной вершины и, присваиваем произвольному ребру uv номер 1. Затем вычёркиваем ребро иv и переходим в вершину v;
б) пусть ω – вершина, в которую мы пришли в результате выполнения предыдущего шага, и k – номер, присвоенный некоторому ребру на этом шаге. Выбираем любое ребро, инцидентное вершине ω, причём мост выбираем только в том случае, когда нет других возможностей; присваиваем выбранному ребру номер k +1 и вычёркиваем его (ребро графа называется мостом, если его удаление увеличивает число компонент).
Этот процесс, называемый алгоритмом Флёрú, заканчивается, когда все рёбра графа вычеркнуты, т.е. занумерованы.
Алгоритм Флёри, несмотря на кажущуюся простоту, имеет следующий нюанс: для того, чтобы не попасть впросак, следует при нумерации рёбер графа реально вычёркивать (стирать) их на графе-дубликате; тогда в оставшейся (после вычёркивания рёбер графа) части графа-дубликата вы реально можете получить ситуацию с мостом, речь о котором идёт в пункте б алгоритма. В противном случае вы можете и не получить эйлеров цикл в эйлеровом (по определению) графе.
3.1.1.3 Заметим, что эйлеровы графы достаточно редки. Это факт доказывает следующая теорема.
Теорема (Р.Рейд, 1962г.). Почти нет эйлеровых графов.
3.1.2 Эйлеровы пути
Эйлеровым путём в графе называется произвольный путь, проходящий через каждое ребро графа в точности один раз, т.е. путь v1, …, vm+1 такой, что каждое ребро 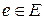 появляется в последовательности v1, …, vm+1 в точности один раз как e={vi,vi+1} для некоторого i. Если v1=vm+1, то такой путь называется эйлеровым циклом. Задача существования эйлерова пути в заданном графе была решена Эйлером в 1736-м году, и представленное им необходимое и достаточное условие существования такого пути (см. следующую теорему) считается первой в истории теоремой теории графов.
появляется в последовательности v1, …, vm+1 в точности один раз как e={vi,vi+1} для некоторого i. Если v1=vm+1, то такой путь называется эйлеровым циклом. Задача существования эйлерова пути в заданном графе была решена Эйлером в 1736-м году, и представленное им необходимое и достаточное условие существования такого пути (см. следующую теорему) считается первой в истории теоремой теории графов.
Теорема. Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более чем две вершины нечётной степени.
Заметим, что концами эйлерова пути являются как раз вершины нечётной степени (если они, конечно же, существуют). Следует также отметить, что не существует графов только с одной вершиной нечётной степени. Действительно, обозначая степень вершины v через d(v), имеем
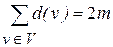 , (3.1)
, (3.1)
потому что в указанную выше сумму каждое ребро {u,v} входит дважды: один раз в d(u), и один раз в d(v) (m – число рёбер в графе). Отсюда следует, что число вершин нечётной степени всегда чётно. Кстати, граф, содержащий эйлеров путь, можно также как и эйлеров граф нарисовать одним рóсчерком, не отрывая карандаша от бумаги, только в этом случае точки начала и окончания рисования не совпадут. Примеры графов, содержащих эйлеровы пути, приведены на рисунке 3.3.
Если в связном графе нет вершин нечётной степени, то каждый эйлеров путь является циклом, так как концы эйлерова пути, не являющегося циклом, всегда вершины нечётной степени.
3.2 Гамильтоновы графы
3.2.1 Гамильтоновы циклы
3.2.1.1 Рассмотрим теперь задачу, рассмотренную в предыдущем подразделе 3.1, с той лишь разницей, что на этот раз нас будут интересовать пути, проходящие в точности один раз через каждую вершину (а не каждое ребро!) данного графа. Эта, на первый взгляд небольшая, модификация приводит к значительному усложнению проблемы.
 |
Граф называется гамильтоновым, если в нём имеется простой цикл (т.е. с разными вершинами, кроме, разумеется, концевых), содержащий каждую вершину этого графа. Сам этот цикл также называется гамильтоновым. Гамильтоновой называют и простую цепь, содержащую каждую вершину графа. Слово «гамильтонов» в этих определениях связано с именем известного ирландского математика У.Гамильтона, который в 1859-м году предложил следующую игру под названием «Кругосветное путешествие». Каждой из двадцати вершин додекаэдра приписано название одного из крупных городов мира. Требуется, переходя из одного города к другому по рёбрам додекаэдра, посетить каждый город в точности один раз и вернуться в исходный город. Эта задача, очевидно, сводится к отысканию в графе додекаэдра (рисунок 3.4, а) простого цикла, проходящего через каждую вершину этого графа (вершины пронумерованы в порядке, в котором они проходятся в одном из возможных гамильтоновых циклов, начиная с вершины 1, т.е. 1-2-3-4-…-18-19-20-1).

Не все связные графы гамильтоновы хотя бы потому, что такой граф должен быть двусвязным. Однако пример графа, представленный на рисунке 3.4, б, показывает, что для гамильтоновости графа его двусвязности недостаточно. Кстати, в графе на рисунке 3.4, б существует гамильтонова цепь (гамильтонов путь), например 1-2-5-8-7-6-3-4, а в графе на рисунке 3.4, в такого пути нет.
Остановимся на понятии двусвязности графа, для чего дадим некоторые определения. Вершина v графа G называется точкой сочленения (или разделяющей вершиной), если граф G–v имеет больше компонент, чем G. В частности, если G связен и v – точка сочленения, то граф G–v не связен. Числом вершинной связности (или просто числом связности) æ(G) графа G называется наименьшее число вершин, удаление которых приводит к несвязному или одновершинному графу. Граф называется k-связным, если æ(G)≥k. В частности, 2-связные (двусвязные) графы – это связные графы без точек сочленения, не являющиеся одновершинными. Двусвязные графы обладают следующими свойствами, вытекающими непосредственно из определения: степени вершин двусвязного графа больше единицы; в двусвязном графе для любых трёх несовпадающих в6ершин a, b, v имеется (a, b)–цепь, не проходящая через v.
3.2.1.2 Несмотря на внешнее сходство постановок, задачи распознавания эйлеровости и гамильтоновости графа принципиально различны. Используя теорему из подпункта 3.1.1.1, легко узнать, является ли граф эйлеровым. В случае положительного ответа алгоритм Флёри позволяет достаточно быстро построить один из эйлеровых циклов.
Что касается гамильтоновости, то ситуация здесь совсем иная. Ответить на вопрос, является ли данный граф гамильтоновым, как правило, очень трудно. Изучение условий гамильтоновости – одно из весьма популярных направлений теории графов. Основная масса доказанных теорем утверждает, что при выполнении определённых условий граф содержит гамильтонов цикл, причём метод доказательства таких теорем обычно даёт и эффективный алгоритм построения самого гамильтонова цикла. Здесь мы приведём несколько теорем (без доказательств) такого рода (достаточных условий гамильтоновости). Интуитивно ясно, что если граф содержит много рёбер и эти рёбра к тому же достаточно равномерно распределены, то граф «предрасположен» быть гамильтоновым. В трёх приводимых ниже теоремах можно усмотреть подтверждение этому.
Теорема (В.Хватал, 1972г.). Граф со степенной последовательностью 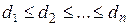 является гамильтоновым, если для всякого k, удовлетворяющего неравенствам
является гамильтоновым, если для всякого k, удовлетворяющего неравенствам 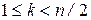 , истинна импликация
, истинна импликация 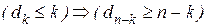 .
.
Напомним, что степенной последовательностью графа называется список степеней его вершин.
Теорема (О.Оре, 1960г.). Если для любой пары несмежных вершин u и v графа G порядка n≥3 выполняется неравенство 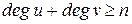 , то G – гамильтонов граф.
, то G – гамильтонов граф.
Теорема (Г.Дирак, 1952г.). Если |G|=n≥3 и для любой вершины v графа G выполняется неравенство 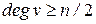 , то G – гамильтонов граф.
, то G – гамильтонов граф.
Если в n-вершинном графе G фиксировать одну вершину и обход всегда начинать с неё, то всякому гамильтонову циклу очевидным образом будет соответствовать перестановка элементов множества вершин VG. Тем самым найти гамильтонов цикл либо убедиться в его отсутствии можно путём перебора (n–1)! перестановок. Если граф G гамильтонов, то проделать этот перебор в полном объёме придётся только в случае крайнего невезения – когда нужная, т.е. отвечающая гамильтонову циклу, перестановка встретится последней в этом процессе. Если же G – негамильтонов граф, то, действуя подобным образом, придётся в любом случае проверить все (n–1)! перестановок.
На практике не пользуются столь бесхитростным способом распознавания гамильтоновости, а применяют различные алгоритмы частичного перебора. Однако и там наблюдается такой же эффект, т.е. негамильтоновость установить, как правило, труднее, чем гамильтоновость. В этой ситуации были бы полезны необходимые условия гамильтоновости. Такие условия нужны и для построения примеров негамильтоновых графов с заданными свойствами. К сожалению, для графов общего вида необходимые условия гамильтоновости неизвестны, за исключением уже упоминавшегося банального факта, что гамильтонов граф должен быть 2-связным. Иначе обстоит дело с планарными графами.
Рамки практического занятия слишком узки для полноценного освещения проблемы существования гамильтоновых циклов. Поэтому остановимся на практическом применении гамильтоновых графов и задач, связанных с ними. Далее мы будем решать одну из этих задач на полном графе, где проблема гамильтоновости графа не возникает.
3.2.1.3 Практические применения гамильтоновых графов связаны прежде всего с широко известной задачей коммивояжера. Она состоит в следующем: коммивояжер должен посетить каждый из заданных п городов по одному разу, выехав из некоторого из этих городов и вернувшись в него же. Требуется найти кратчайший маршрут, зная расстояния между каждой парой городов.
Математическая постановка этой задачи выглядит так: в полном взвешенном графе требуется найти гамильтонов цикл (или цепь, если возвращаться в исходную вершину не требуется) минимального веса. Под весом цикла понимается сумма весов составляющих его рёбер.
Например, при производстве печатных плат сверлильный станок с числовым программным управлением (ЧПУ) должен сделать большое количество отверстий в заданных точках платы, переходя от одной точки к другой. Время работы такого станка складывается из суммарного времени сверления, которое не зависит от порядка обхода точек, и из суммарного времени переходов от одной точки к другой. Требуется задать такую последовательность обхода точек, чтобы общее время работы станка было минимально. Легко видеть, что это – задача коммивояжера.
Представление о непосредственных применениях гамильтоновых цепей даёт следующая ситуация: имеется машина (станок, компьютер) и п заданий, каждое из которых она способна выполнить после соответствующей настройки. При этом необходимо затратить на переналадку tij единиц времени для того, чтобы после выполнения i-го задания выполнить j-е. В предположении, что tij=tji,требуется найти последовательность выполнения заданий, при которой время каждой переналадки не превосходит величины t. Если построить граф G, у которого VG={1, 2, ...,n}, EG={ij: tij<t }, то наша задача сведётся к отысканию гамильтоновой цепи в этом графе.
Кстати, если в постановке предыдущей задачи допустить, что tij≠tji, то мы имеем дело с поиском гамильтонова цикла в орграфе (см. подпункт 3.2.1.5). Именно такую задачу мы и рассмотрим в пункте 3.2.2.
3.2.1.4 В заключение отметим без доказательства теорему, отражающую широкую распространённость гамильтоновых графов.
Теорема (В.А.Перепелица, 1969г.). Почти все графы гамильтоновы.
3.2.1.5 Определения эйлеровых и гамильтоновых ориентированных графов сходны с аналогичными определениями для неориентированных.
Цепь, содержащая каждую дугу орграфа, называется эйлеровой. Связный орграф называется эйлеровым, если в нём есть замкнутая эйлерова цепь. Приведём без доказательства теорему об эйлеровости орграфа.
Теорема. Для связного ориентированного графа G следующие утверждения равносильны:
1) граф G эйлеров;
2) для любой вершины 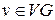 верно равенство
верно равенство 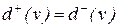 ;
;
3) граф G является объединением контуров, попарно не имеющих общих рёбер.
Контур (путь) орграфа G называется гамильтоновым, если он содержит все вершины G. Гамилътонов орграф – это орграф, имеющий гамильтонов контур. Вопросы, связанные с распознаванием гамильтонового орграфа и построением гамильтоновых контуров или сетей, являются столь же сложными, как и аналогичные вопросы для неориентированных графов. Приведём без доказательств одно из достаточных условий гамильтоновости орграфа.
Теорема (М.Мейниел, 1973г.). Пусть G – сильный орграф порядка n>1 без петель и параллельных дуг. Если для любой пары u и v его несовпадающих несмежных вершин справедливо неравенство degu+degv>2n–1, то в G есть гамильтонов контур.
3.2.2 Задача о переналадке линии
3.2.2.1 На автоматической линии необходимо обработать n партий деталей. Время наладки линии для обработки очередной партии зависит от того, какая партия деталей обрабатывалась перед данной партией. Продолжительность переналадок заданы матрицей [tij], где элемент tij означает время переналадки при переходе от партии i к партии j. Требуется определить порядок обработки деталей, при котором затраты времени на переналадку были бы минимальными.
Задачу будем решать методом ветвей и границ с использованием для оценки границ задачи об оптимальных назначениях. В результате решения должно быть определено минимальное время, необходимое на выполнение переналадок, и порядок обработки партий деталей, при котором достигается это (минимальное) время.
С математической точки зрения настоящая задача эквивалентна задаче коммивояжёра (см. подпункт 3.2.1.3), которая служит моделью многих задач календарного планирования, маршрутизации перевозок и т.п. Задача коммивояжёра заключается в следующем. Имеется n городов, расстояние между которыми заданы матрицей [cij]n×n; коммивояжёр должен побывать в каждом городе один раз и вернуться в начальный пункт маршрута, совершив путь минимальной длины. В понятиях теории графов задача состоит в том, чтобы найти кратчайший простой цикл из n рёбер с n вершинами при заданных длинах cij рёбер (i,j).
Если сопоставить партиям деталей городá, а матрице времён переналадок [tij]n×n матрицу расстояний[cij]n×n между городами, и считать, что по завершении всех обработок линия возвращается в исходное состояние, то очевидно, что задача о переналадке линии математически совпадает с задачей коммивояжёра.
3.2.2.2 Приведём общую схему метода ветвей и границ для задачи коммивояжёра. Обозначим через Р множество всех простых циклов (без повторяющихся вершин) из n рёбер, среди которых отыскивается кратчайший. Пусть имеется некоторая вспомогательная (оценочная) задача, из решения которой может быть получена оценка (нижняя граница) φ длины кратчайшего цикла на множестве Р или на любом его подмножестве Рi. Для полного описания метода следует указать способ вычисления нижней границы и правило ветвления подмножеств. Одним из способов получения оценок для вершин дерева ветвлений может служить решение задач об оптимальных назначениях, получаемых из задачи коммивояжёра релаксацией (неучётом) условия связности маршрута. Тогда допустимым решением задачи о назначениях является любая совокупность независимых элементов матрицы [cij]n×n, из которых никакие два элемента не лежат в одном ряду. Постановка же задачи об оптимальных назначениях следующая: имеется n различных работ, которые могут быть поручены n различным исполнителям; назначение исполнителя i на работу j связано с затратами cij, причём каждый исполнитель должен быть назначен на одну (и только одну!) работу так, чтобы суммарные затраты на выполнение всех работ были минимальны. Для задачи коммивояжёра допустимыми будут лишь те из этих совокупностей, (речь идёи о допустимых решениях задачи о назначениях), в которых независимые «клетки» (i,j), (j,k), (k,l), …, (n,i) образуют последовательность, позволяющую построить цикл, проходящий через все города в некотором порядке (i,j,k,l,…,n,i).
Теперь опишем, как практически осуществлять ветвление. Пусть на исходной матрице [cij]n×n ([tij]n×n) решена оценочная задача об оптимальных назначениях. Результатом её решения может быть либо связный цикл, проходящий через все города (вершины графа), либо совокупность подциклов (что более вероятно), каждый из которых проходит через часть городов. В первом случае задача коммивояжёра решена; во втором случае переходим к её ветвлению. Для этого выберем один из подциклов, предпочтительно с наименьшим числом вершин. Одну из дуг этого подцикла, например (k,l), используем для получения двух новых задач назначения. В одной из них элемент ckl=0, а все остальные элементы строки k и столбца l заменяются на ∞. Это означает, что из города k обязателен переезд в город l; для запрещения же подцикла (k,l,k), т.е. запрещения обратного переезда из l в k, полагаем также clk=∞. В другой задаче, наоборот, элемент ckl=∞, clk=0, а все остальные элементы строки остаются без изменения. Это означает, что переезд из города k непосредственно в город l запрещён, но обязателен обратный переезд (из l в k). Из решений данных задач получаются оценки соответствующих им подмножеств [одно из них без ребра (l,k), т.е. это обозначается ( 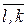 ); другое – без ребра (k,l); это обозначается (
); другое – без ребра (k,l); это обозначается ( 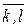 )]; они сравниваются между собой и если наименьшая из них получена на гамильтоновом цикле (т.е. простом цикле, включающем все вершины графа задачи), то исходная задача решена. В противном случае процесс ветвления и оценивания продолжается аналогичным образом до получения цикла с длиной не большей, чем нижние границы на всех висячих вершинах дерева решений (они содержат допустимые решения задачи коммивояжера). При этом необходимо, чтобы при ветвлении любого множества были испытаны все альтернативы, связанные с запрещением дуг подцикла, используемого при ветвлении. Другими словами, к моменту останова каждая разветвляемая вершина дерева решений должна содержать столько потомков, сколько имеется дуг в подцикле, выбранном для её ветвления.
)]; они сравниваются между собой и если наименьшая из них получена на гамильтоновом цикле (т.е. простом цикле, включающем все вершины графа задачи), то исходная задача решена. В противном случае процесс ветвления и оценивания продолжается аналогичным образом до получения цикла с длиной не большей, чем нижние границы на всех висячих вершинах дерева решений (они содержат допустимые решения задачи коммивояжера). При этом необходимо, чтобы при ветвлении любого множества были испытаны все альтернативы, связанные с запрещением дуг подцикла, используемого при ветвлении. Другими словами, к моменту останова каждая разветвляемая вершина дерева решений должна содержать столько потомков, сколько имеется дуг в подцикле, выбранном для её ветвления.
3.2.2.3 Приведём алгоритм решения задачи об оптимальных назначениях, состоящий из начального и общего шагов.
Начальный шаг: выполняем эквивалентное преобразование матрицы С так, чтобы получить матрицу, в которой в каждой строке и каждом столбце имеется хотя бы один ноль; для этого просмотрим каждую строку матрицы С, найдём в ней наименьший элемент и вычтем его из элементов этой строки; полученная при этом матрица С1 называется приведенной по строкам; в матрице С1 просмотрим все столбцы, найдём в каждом из них минимальный элемент и вычтем его из элементов просматриваемого столбца; полученная при этом матрица С2 будет приведенной по строкам и столбцам; клетку, содержащую ноль, будем считать допустимой; при каждом назначении делаем отметку (ставим, например, звёздочку) в соответствующей допустимой (нулевой) клетке; закончив просмотр всех строк, переходим к общему шагу.
Общий шаг состоит из двух шагов:
– шаг 1 – решаем упрощённую задачу о назначениях (расставляем звёздочки среди допустимых клеток); при этом возможны два случая:
а) назначения получают все n исполнителей;
б) назначения получают не все n исполнителей.
В случае а исходная задача о назначениях решена; в случае же б переходим к шагу 2, предварительно сделав пометку строк и столбцов матрицы. [Пометим чёрточкой все строки, не содержащие звёздочки. Затем возьмём какую-либо помеченную строку, например i-ую, и просмотрим её, отыскивая допустимые непомеченные клетки (т.е. нулевые без звёздочки). Столбцы, содержащие такие клетки, пометим номером просматриваемой строки, в данном случае номером i. Будем повторять это до тех пор, пока не просмотрим все помеченные (чёрточкой) строки. Столбец, уже получивший какую-нибудь пометку, больше не помечается.
Теперьвыберем любой помеченный столбец, например j-й, и просмотрим его, отыскивая звёздочку. Если она (звёздочка) будет найдена, пометим строку, в которой стоит эта звёздочка, номером просматриваемого столбца, в данном случае j. Снова выберем какой-либо помеченный непросмотренный столбец и повторим эту операцию. После того как будут просмотрены все помеченные столбцы, переходим к просмотру вновь отмеченных строк, отыскивая в них допустимые невыделенные клетки, и т.д. Продолжаем этот процесс, попеременно просматривая строки и столбцы, пока не достигнем следующего: 1) либо будет помечен столбец, не содержащий звёздочки; 2) либо приписать никаких пометок больше нельзя и все помеченные столбцы содержат звёздочки.
В случае 1 общее число звёздочек (назначений) увеличиваем следующим образом. В помеченном столбце, не содержащем звёздочки, поставим звёздочку в клетке, указываемой пометкой этого столбца. Затем в строке, где проставлена новая звёздочка, уберём прежнюю из клетки, указываемой пометкой этой строки. В столбце, в котором находится удаляемая звёздочка, перейдём к клетке, указываемой его пометкой и поставим звёздочку и т.д. В конце концов придём к одной из строк, помеченных чёрточкой, и общее число звёздочек в таблице возрастёт на единицу. После этого сотрём пометки, повторим процесс расстановки пометок и вновь переместим звёздочки, продолжая процесс до тех пор, пока не придём к случаю 2, в котором оптимальное закрепление достигнуто. Минимальное число рядов, содержащих все допустимые клетки, состоит из непомеченных строк и помеченных столбцов].
– шаг 2 – зачеркнём каждую непомеченную строку и каждый помеченный столбец; далее рассмотрим часть матрицы, состоящую из незачёркнутых элементов и возьмём наименьшее число в ней (т.е. в этой части матрицы); вычтем это число из всех незачёркнутых элементов и прибавим к дважды зачёркнутым элементам (т.е. к элементам, стоящим на пересечении зачёркнутой строки с зачёркнутым столбцом); переходим к шагу 1 общего шага.
3.2.2.4 Итак, решим нашу задачу о переналадке линии в терминах задачи коммивояжёра, используя для оценивания подмножеств задачу об оптимальном назначении. Задачу об оптимальном назначении будем решать в соответствии с вышеприведенным алгоритмом.
Вначале в списке задач-кандидатов находится одна задача коммивояжёра, заданная матрицей (таблица 3.1) (n=5) на всём множестве циклов Р. Решаем её релаксацию – задачу о назначениях. Для этого приводим исходную матрицу сначала по строкам (таблица 3.2), затем – по столбцам (таблица 3.3).
Далее решаем упрощённую задачу о назначениях. В матрице из таблицы 3.3 в каждой строке и столбце имеются нулевые элементы. Назначение
Таблица 3.1 – Исходные данные задачи о переналадке линии
В единицах времени
| i j | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ |
Таблица 3.2
| i j | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ |
Таблица 3.3
| i j |  4 4
| |||||
| ∞ | 0* | |||||
 3 3
| ∞ | 0* | ||||
| ∞ | – | |||||
 3 3
| 0* | ∞ | ||||
 0* 0*
| ∞ | |||||
получат 4 исполнителя. Помечаем строки и столбцы. Минимальное множество рядов, содержащих все допустимые клетки, составляют непомеченные строки 2, 4, 5 и помеченный столбец 4. Зачеркнув их, находим среди элементов, оставшихся незачёркнутыми, наименьший (он равен 1). Вычитаем этот элемент из всех незачёркнутых и прибавляем его к дважды зачёркнутым элементам; остальные элементы остаются без изменений. Получаем матрицу, представленную в таблице 3.4. В этой матрице также назначение получат 4 исполнителя, причём такое же, как и в предыдущем случае (см. таблицу 3.3). Над матрицей из таблицы 3.4 проделываем аналогичные действия и получаем
Таблица 3.4
| i j |  3 3
|  4 4
|  5 5
| |||
| ∞ | 0* | |||||
| ∞ | 0* | |||||
| ∞ | – | |||||
| 0* | ∞ | |||||
 0* 0*
| ∞ | |||||
решение задачи о назначениях (таблица 3.5).
Таблица 3.5
| i j | ||||||
| ∞ | 0* | |||||
| ∞ | 0* | |||||
| ∞ | 0* | |||||
| 0* | ∞ | |||||
| 0* | ∞ | |||||
В таблице 3.5 назначение получают все 5 исполнителей: (1.2), (2,5), (3,4), (4,3), (5,1), отмеченные звёздочками. Рассматривая эту последовательность клеток как решение задачи коммивояжёра, перепишем его так, чтобы номер строки в записи последующей клетки совпадал с номером столбца предыдущей. Тогда получим две последовательности, задающие порядок обхода городов в виде двух подциклов (1,2), (2,5), (5,1) и (3,4), (4,3), или короче – (1,2,5,1) и (3,4,3). Суммирование соответствующих элементов исходной таблицы 3.1 даёт величину затрат, связанных с данным распределением:
Z=15+12+11+14+15=67. (3.2)
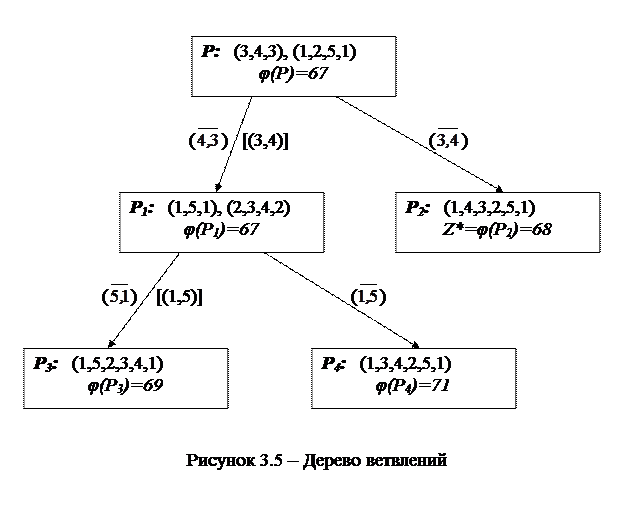
Таким образом, исследовано допустимое множество Р задачи коммивояжёра и при этом нижняя граница φ(Р)=67 длины искомого кратчайшего цикла получена на элементе, не входящем в множество Р. Переходим к ветвлению множества Р. Для этого выбираем подцикл с мéньшим числом вершин, т.е. подцикл (3,4,3), и вносим в список задач-кандидатов две задачи коммивояжёра. Одна из них строится на подмножестве Р1 всех циклов, где запрещён переезд из пункта 4 в пункт 3 (но обязателен переезд из 3 в 4; для этого записываем в таблице 3.6 элемент с43=∞, а в 3-ей строке все элементы, кроме с34, полагаем равными ∞,), другая – на подмножестве всех циклов Р2, не содержащих дугу (3,4) [обозначение при ветвлении – ( 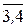 )]. Решение задачи на подмножестве Р1 получается прямо в исходной для этой задачи таблице 3.6 и имеет вид: (1,5,1), (2,3,4,2), причём затраты на это распределение составляют
)]. Решение задачи на подмножестве Р1 получается прямо в исходной для этой задачи таблице 3.6 и имеет вид: (1,5,1), (2,3,4,2), причём затраты на это распределение составляют
φ(Р1)=14+12+11+15+15=67. (3.3)
Таблица 3.6
| i j | ||||||
| ∞ | ∞ | 0* | ||||
| ∞ | 0* | ∞ | ||||
| ∞ | ∞ | ∞ | 0* | ∞ | ||
| 0* | ∞ | ∞ | ||||
| 0* | ∞ | ∞ | ||||
Исходная матрица для задачи о назначениях, решаемой на подмножестве Р2, сформирована на основании на основании таблицы 3.5 и представлена в таблице 3.7 (в ней в отличие от таблицы 3.5 элемент с34=∞).
Таблица 3.7
| i j | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ | ∞ | |||||
| ∞ | ||||||
| ∞ | ||||||
Путём приведения её по третьей строке получим матрицу (таблица 3.8), содержащую решение этой задачи: простой цикл (1,4,3,2,5,1) длиной (см. таблицы 3.8 и 3.1)
φ(Р2)=13+12+14+14+15=68. (3.4)
Таблица 3.8
| i j | ||||||
| ∞ | 0* | |||||
| ∞ | 0* | |||||
| 0* | ∞ | ∞ | ||||
| 0* | ∞ | |||||
| 0* | ∞ | |||||
Задачу Р2 исключаем из списка задач-кандидатов, запомнив цикл и его длину соответственно как решение-претендент и рекорд, а задачу Р1 разветвляем на две подзадачи с множеством Р3 и Р4. Множество Р3 включает все циклы, где запрещены дуги (4,3) и (5,1); а множество Р4 – все циклы, в которые не входят дуги (4,3) и (1,5). Формулируем две задачи назначения. Задача на множестве Р3 представлена в таблице 3.9 и получена из таблицы 3.6.
Таблица 3.9
| i j | ||||||
| ∞ | ∞ | ∞ | ∞ | |||
| ∞ | ∞ | ∞ | ||||
| ∞ | ∞ | ∞ | ∞ | |||
| ∞ | ∞ | ∞ | ||||
| ∞ | ∞ | ∞ | ||||
Если таблицу 3.9 привести по первому столбцу, то уже в следующей таблице 3.10 содержится решение задачи Р3: простой цикл (1,5,2,3,4,1) длиной (см. таблицы 3.10 и 3.1)
φ(Р3)=14+12+11+18+14=69, (3.5)
который, однако, не ставится новым решением-претендентом для задачи коммивояжёра, поскольку его длина больше имеющегося рекорда [см. (3.4)].
Таблица 3.10
| i j | ||||||
| ∞ | ∞ | ∞ | ∞ | 0* | ||
| ∞ | 0* | ∞ | ∞ | |||
| ∞ | ∞ | ∞ | 0* | ∞ | ||
| 0* | ∞ | ∞ | ∞ | |||
| ∞ | 0* | ∞ | ∞ | |||
Матрица для задачи о назначениях на подмножестве Р4 составляется на основе таблицы 3.6 и представлена в таблице 3.11. После необходимых её преобразований (таблицы 3.12, 3.13) получаем решение задачи (см. таблицу 3.13) в виде гамильтонова цикла (1,3,4,2,5,1) длиной (см. таблицы 3.1 и 3.13)
φ(Р4)=18+12+11+15+15=71. (3.6)
Задача Р4, как и задача Р3, не является решением-претендентом, поскольку её нижняя оценка хуже, чем у задачи Р2.
Таблица 3.11
| i j |  2 2
| |||||
| ∞ | 0* | ∞ | ∞ | |||
 2 2
| ∞ | ∞ | 0* | |||
 ∞ ∞
| ∞ | ∞ | 0* | ∞ | ||
| ∞ | ∞ | – | ||||
 0* 0*
| ∞ | ∞ | ||||
Таблица 3.12
| i j |  1 1
|  2 2
| ||||
| ∞ | 0* | ∞ | ∞ | |||
 2 2
| ∞ | ∞ | 0* | |||
 ∞ ∞
| ∞ | ∞ | 0* | ∞ | ||
| ∞ | ∞ | – | ||||
| 0* | ∞ | ∞ | ||||
Таблица 3.13
| i j | ||||||
| ∞ | 0* | ∞ | ∞ | |||
| ∞ | ∞ | 0* | ||||
| ∞ | ∞ | ∞ | 0* | ∞ | ||
| 0* | ∞ | ∞ | ||||
| 0* | ∞ | ∞ | ||||
После решения перечисленных задач имеем три висячие вершины дерева ветвлений – Р2, Р3 и Р4 (рисунок 3.5), не требующие дальнейшего ветвления, и при ветвлении вершин Р и Р1 испытаны все альтернативы, связанные с подциклами (3,4,3) и (1,5,1), выбранными для ветвления. Из всех оценок висячих вершин оценка φ(Р2)=68 наименьшая и получена на цикле (1,4,3,2,5,1), проходящем через все вершины графа. Следовательно, этот цикл оптимален.
В терминах задачи о переналадке линии оптимальное решение задачи коммивояжёра выглядит следующим образом: при обработке пяти партий деталей суммарное время переналадки будет минимальным и составит Z*=68, если после первой партии деталей обрабатывать четвёртую, затем третью, вторую, пятую и возвратить линию в исходное состояние готовности обрабатывать первую партию деталей.
Варианты заданий
Задание №1
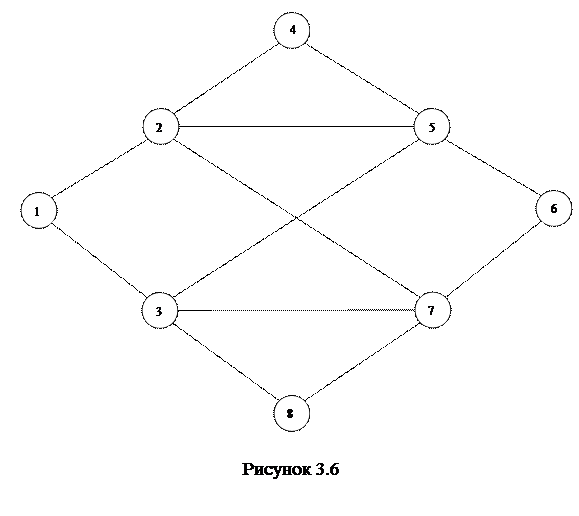
Найти эйлеров цикл в графе, представленном на рисунке 3.6.
Задание №2
На автоматической линии необходимо обработать n=5 партий деталей. Время наладки линии для обработки очередной партии зависит от того, какая партия деталей обрабатывалась перед данной партией. Продолжительности переналадок заданы матрицей [tij]n×n (таблица 3.14), где элемент tij означает время переналадки при переходе от партии i к партии j. Требуется определить порядок обработки партий деталей, при котором затраты времени на переналадку были бы минимальными.
Таблица 3.1 – Исходные данные задачи о переналадке линии
В единицах времени
| i j | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ |
Указания. Задача должна быть решена методом ветвей и границ с использованием для оценки границ задачи об оптимальных назначениях. В результате решения задачи должно быть определено минимальное время, необходимое для выполнения переналадок, и порядок обработки партий деталей, при котором достигается это время. Пояснить, почему полученное решение является оптимальным.
Задание №3
Для графа, представленного на рисунке 3.7, и заданной матрицы весов
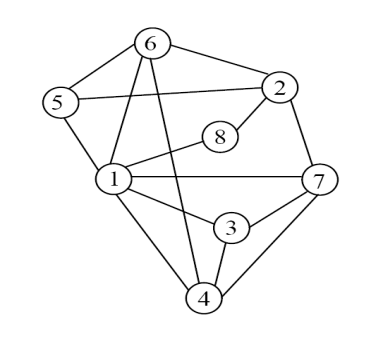
Рисунок 3.7

[cij]8×8=
решить задачу коммивояжёра.
Остальные задачи для практических занятиях по данной теме будут предлагаться преподавателем.
| <== предыдущая лекция | | | следующая лекция ==> |
| Коэффициенты ковариации и парной корреляции | | | Поняття та соціально-економічна сутність трудового потенціалу |
Дата добавления: 2016-05-25; просмотров: 2809;
