Общие понятия термодинамики
Всякое тело обладает определенной внутренней энергией, зависящей только от его состояния. Внутренняя энергия тела – это сумма многих составляющих, в том числе внутриатомной и внутриядерной энергий. Но в термодинамике принимают в расчет только те виды внутренней энергии, которые изменяются в термодинамических процессах. К этим видам энергии относятся:
- внутренняя кинетическая энергия – энергия поступательного, вращательного и колебательного движения молекул (атомов) тела;
- внутренняя потенциальная энергия – энергия, зависящая от взаимного положения частиц тела и связанная с силами межмолекулярного (межатомного) притяжения и отталкивания.
Внутренняя энергия тела зависит от его массы, температуры и вещества, из которого состоит тело, а для постоянной массы одного и того же вещества внутренняя энергия тела зависит только от его температуры.
Так как внутренняя энергия тела может изменяться – уменьшаться или увеличиваться, то изменение внутренней энергии тела зависит только от изменения температуры. И чем больше изменение температуры тела, тем значительнее изменение его внутренней энергии.
Для описания состояния термодинамической системы вводятся физические величины, которые называются термодинамическими параметрами или параметрами состояния системы.
Обычно к термодинамическим параметрам системы относят:
давление –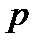 
;
температуру –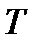 
;
удельный объем–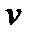 
.
Давлением называется физическая величина, численно равная силе, действующей на единицу площади поверхности тела по направлению внешней нормали к этой поверхности:
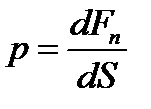
, [Па]
Давление обусловлено взаимодействием молекул рабочего тела с поверхностью и измеряется с помощью манометров, барометров и вакуумметров.
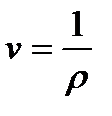Удельный объем–это объем единицы массы вещества или величина, обратная плотности ( 
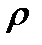) тела:
, [м3/кг]
Для однородного тела удельный объем равен объему тела, масса которого равна единице.
Температурой называется физическая величина, характеризующая степень нагретости тела.
Температура является мерой интенсивности теплового движения молекул (атомов, ионов) тела. Температуру тела можно измерять только косвенным путем, основываясь на том, что целый ряд физических свойств тела, поддающихся прямому или косвенному измерению, зависит от температуры (например, при изменении температуры тела изменяются его линейные размеры и объем, плотность, электрическое сопротивление, упругие свойства и т.д.)
Термодинамическое состояние любого тела полностью определяется любыми двумя вышеперечисленными параметрами. Все параметры состояния связаны между собой уравнениями состояния:
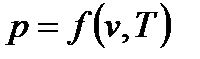
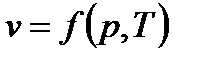
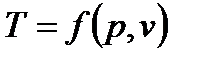
Наиболее известным из уравнений состояния является уравнение Менделеева-Клапейрона:
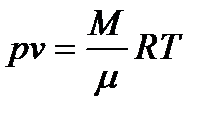
где:
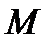– масса вещества;
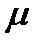– молярная масса вещества (отношение массы вещества к количеству молей, которое в нем содержится);
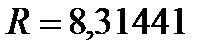[Дж/(моль∙К)] – универсальная газовая постоянная. Универсальность R вытекает из закона Авогадро, согласно которому моли всех идеальных газов при одинаковых давлениях и температурах занимают одинаковые объемы;
Для 1 кг однородного газа уравнение состояния примет вид:
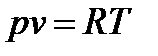
Если состояние любой термодинамической системы можно определить по любым двум вышеперечисленным параметрам (вычислив третий параметр по уравнению состояния), то вполне реально изобразить термодинамическое состояние вещества графически: виде точки на плоскости в системе координат.
Исходя из рассмотренных выше основных термодинамических параметров состояния вещества (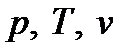 
), возможны следующие варианты систем координат, связанных с параметрами состояния (рис. 4):
          
|
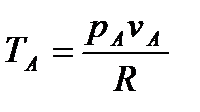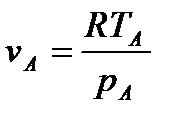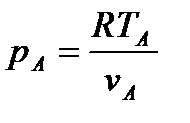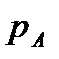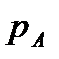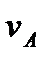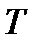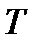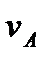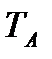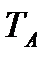
Рис. 4. Системы координат, связанные с термодинамическими параметрами
состояния вещества
Каждой точке на диаграмме соответствует свое состояние вещества, характеризуемое значениями термодинамических параметров при проекции на оси координат, и третьим параметром, связанным с ними уравнением термодинамического состояния вещества (рис. 4).
Если все термодинамические параметры постоянны во времени и одинаковы для всех точек термодинамической системы, то такая система называется равновесной. Если между различными точками в системе существуют разности температур, давлений и других параметров, то эта система является неравновесной. В неравновесной системе под действием градиентов параметров всегда существуют потоки теплоты и вещества, стремящиеся вернуть систему в состояние равновесия.
Еще одним важным термодинамическим параметром состояния вещества является энтропия, характеризующая количество теплоты, подведенной к телу или отведенной от него:
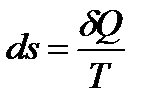, [Дж/К]
Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух других параметров состояния:
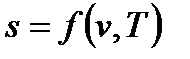
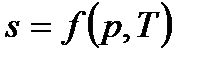
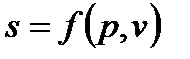
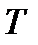
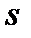
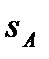
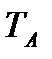
и с понятием «энтропия» также можно связать системы координат, отображающие термодинамическое состояние тела. Наиболее часто в термодинамике используются диаграммы 
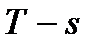(рис. 5), в которых удобно изображать термодинамические процессы, происходящие в различного рода тепловых двигателях – газотурбинных и паросиловых установках.
Рис. 5. Система координат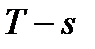 
.
При рассмотрении различных термодинамических процессов представляет интерес не абсолютное значение энтропии, а ее изменение в этих процессах. Поэтому обычно пользуются относительным значением энтропии вещества, рассчитанным относительно произвольно выбранной точки отсчета.
В термодинамике важную роль играет сумма внутренней энергии системы –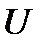 
и произведения давления системы на ее объем, называемая энтальпией:
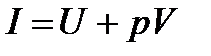[Дж];
Удельная энтальпия (отнесенная к единице массы) представляет собой энтальпию системы, содержащей 1 кг вещества:
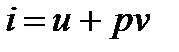[Дж/кг];
Так как входящие в энтальпию величины являются функциями состояния, то она также может быть представлена в виде функции двух любых параметров состояния:
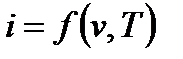
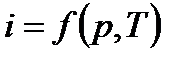
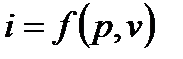
и энтальпию, как и энтропию, так же можно связать с другими параметрами состояния через системы координат.
В теплотехнике наиболее часто используют систему координат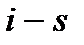 
–«энтальпия – энтропия» (рис. 6).
     
|
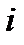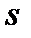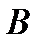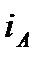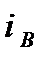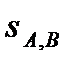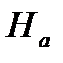
При расчетах практический интерес представляет изменение энтальпии в конечном процессе.
Изменение энтальпии в любом процессе не зависит от характера процесса, а определяется только начальным и конечным состояниями тела.
Разность энтальпий между начальным и конечным термодинамическими состояниями тела, вычисленная в диаграмме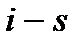 
называется теплоперепадом – Нa: Рис. 6. Система координат i– s.
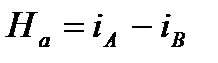[Дж/кг];
В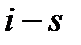 
диаграммах очень удобно изображать термодинамические процессы, происходящие с водой и водяным паром, поэтому такие диаграммы всегда используют для инженерных расчетов и построений термодинамических процессов при проектировании паросиловых установок.
Важным термодинамическим свойством вещества является его теплоемкость.
Теплоемкостью тела – С, называется физическая величина, численно равная отношению количества теплоты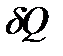 
, сообщаемого телу, к изменению температуры тела 
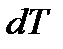в данном термодинамическом процессе:
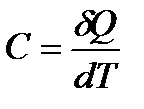, [Дж/К];
т. е. теплоемкость показывает, какое количество теплоты необходимо передать телу для его нагревания на 1 К (1 оС).
Значение теплоемкости зависит от массы вещества, его химического состава, термодинамического состояния и процесса, в котором сообщается или отбирается теплота, поэтому на практике обычно рассматривается удельная теплоемкость вещества, отнесенная к единице массы:
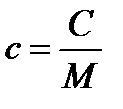, [Дж/кг×К];
Так как теплоемкость вещества зависит от характера протекаемого термодинамического процесса, то в термодинамике при расчетах различают:
теплоемкость при постоянном давлении: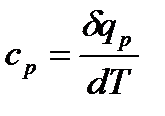 
равную отношению количества теплоты, сообщенной телу при постоянном давлении, к изменению температуры тела;
теплоемкость при постоянном объеме: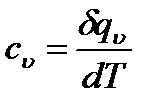 
равную отношению количества теплоты, подведенной к телу при постоянном объеме, к изменению температуры тела.
Численные значения теплоемкости для каждого конкретного вещества и определенных условий можно найти в специальных таблицах.
Дата добавления: 2016-05-25; просмотров: 1060;