Расчет ширины раскрытия трещин, нормальных к продольной оси элемента. 9.3.11 Ширину раскрытия нормальных трещин определяют по формуле (8.128), в которой значение напряжений σs в растянутой арматуре изгибаемых предварительно
9.3.11 Ширину раскрытия нормальных трещин определяют по формуле (8.128), в которой значение напряжений σs в растянутой арматуре изгибаемых предварительно напряженных элементов от внешней нагрузки определяют по формуле
0138S10-03623
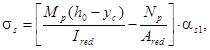(9.38)
где Ired, Ared, ус - момент инерции, площадь приведенного поперечного сечения элемента и расстояние от наиболее сжатого волокна до центра тяжести приведенного сечения, определяемые с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры согласно 8.2.27, принимая в соответствующих формулах значения коэффициента приведения арматуры к бетону αs2 = αs1.
Np - усилие предварительного обжатия (9.3.4);
Мр - изгибающий момент от внешней нагрузки и усилия предварительного обжатия, определяемый по формуле
Mp = M ± Np × eop, (9.39)
где еор - расстояние от точки приложения усилия предварительного обжатия Np до центра тяжести приведенного сечения.
Знак «минус» в формуле (9.39) принимают, когда направления вращений моментов М и Np × eop не совпадают, и «плюс» - когда совпадают.
Допускается напряжение σs определять по формуле
0138S10-03623
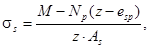(9.40)
где z - расстояние от центра тяжести арматуры, расположенной в растянутой зоне сечения, до точки приложения равнодействующей усилий в сжатой зоне элемента;
esp - расстояние от центра тяжести той же арматуры до точки приложения усилия Np.
Для элементов прямоугольного поперечного сечения при отсутствии (или без учета) сжатой арматуры значение z определяют по формуле
z = h0 - xN/3. (9.41)
где xN - высота сжатой зоны, определяемая согласно 8.2.28 с учетом действия усилия предварительного обжатия Np.
Для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечного сечения допускается значение z принимать равным 0,7h0.
Напряжения σs, определяемые по формулам (9.38), (9.40), не должны превышать (Rs,ser - σsp).
Дата добавления: 2016-05-25; просмотров: 705;