Решение и геометрическая интерпретация игры (2x2).

Если игра (2х2) имеет седловую точку, то ее решение очевидно. Пусть игра без седловой точки с платежной матрицей (a_ij)₂_x₂. Требуется найти оптимальные смешанные стратегии игроков 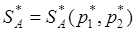и и 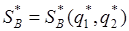цену игры g. В игре (2х2) без седловой точки обе стратегии игроков являются активными. Поэтому в соответствии с теоремой об активных стратегиях, если игрок А будет применять свою оптимальную смешанную стратегию, то независимо от действия игрока В, выигрыш его будет равен цене игры g.

Пусть игрок А использует стратегию 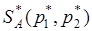, а игрок В – стратегию В₁. Тогда выигрыш игрока А определяется из уравнения

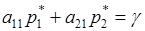Если же игрок В будет применять стратегию В₂, то выигрыш игрока А не изменится и будет определяться равенством

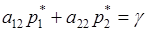Принимая во внимание условие 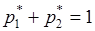, можно записать систему уравнений с тремя неизвестными величинами:

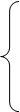
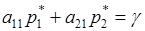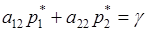, (1)

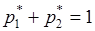Решив эту систему уравнений, находим оптимальную смешанную стратегию 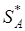игрока А, т.е. 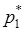и .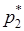

Аналогично определяется оптимальная стратегия 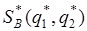игрока В из системы уравнений:

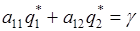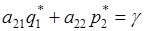, (2)

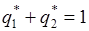В результате решения системы уравнений (2) находятся вероятност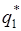и и 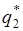, т.е. оптимальная стратегия .

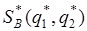Игра (2х2) допускает простую геометрическую интерпретацию. Для этого в системе координат хОу на оси абсцисс откладывается отрезок [А₁,А₂], равный единице, и через концы этого отрезка проводятся перпендикулярные к оси абсцисс прямые, на которых откладываются выигрыши игрока А (рис.1).

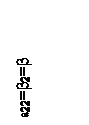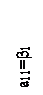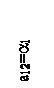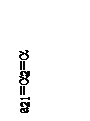Левый перпендикуляр, совпадающий с осью ординат, соответствует стратегии А₁, для которой Р₁=1, Р₂=0, а правый равен стратегии А₂, для которой Р₁=0, Р₂=1. При применении игроком В стратегии В₁ выигрыш будет а₁₁, если игрок А использует стратегию А₁, и будет а₂₁, если он применяет стратегию А₂. Отложив отрезки, равные а₁₁ и а₂₁ на соответствующих перпендикулярах получим две точки: В₁ соответствующий стратегии А₁ и В₁ соответствующий стратегии А₂. Ордината любой точки отрезка В₁В₂ равна величине выигрыша игрока А при применении им стратегии А₁ и А₂ с вероятностями Р₁ и Р₂.

Если игрок В применяет стратегию В₂, то выигрыш игрока А равен а₁₂ при использовании стратегии А₁, и а₂₂ – стратегии А₂. Ординаты точек, лежащие на отрезке В₂В₂, равны среднему выигрышу игрока А, если он применяет стратегии А₁ и А₂ с вероятностями Р₁ и Р₂, а противник -–стратегию В₂.

Для нахождения оптимальной стратегии 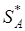построим нижнюю границу выигрыша игрока А, т.е. ломаную В₂NB₁, отмеченную на рис.1 линией. Очевидно, что на этой ломанной лежат минимальные выигрыши игрока А при использовании им любой смешанной стратегии.

Оптимальное решение игры определяет точка N, в которой выигрыш игрока А принимает наибольшее значение (проигрыш игрока В наименьшее значение) равный цене игры g. Проекция этой точки на ось абсцисс соответствует оптимальной стратегии 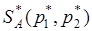, при этом расстояния от точки 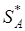до концов единичного отрезка на оси абсцисс равны вероятностям 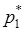и .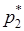

Оптимальная стратегия 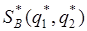игрока В находится аналогично. Для этого необходимо поменять местами игроков А и В. (см. рис.2)

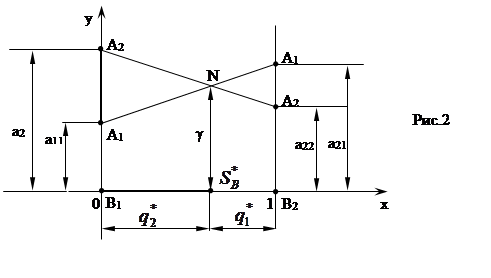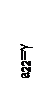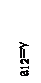На рис.1 и 2 решение игры определялось точкой пересечения стратегий, однако это справедливо не всегда. Так, например на рис.3 показан случай, когда нижняя граница выигрыша игрока А совпадает с отрезком В₂В₂, т.е. стратегия В₁ для игрока В заведомо не выгодная. Здесь

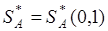, игра имеет седловую точку.

На рис.4 показан случай, в котором 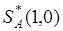, 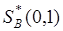. Игра имеет седловую точку.

Дата добавления: 2016-05-16; просмотров: 661;