Решение игры (2хn) и (mx2).

Существует теорема, которая гласит: любая конечная игра с нулевой суммой (mxn) имеет решение, в котром число активных стратегий каждого игрока не превосходит l, где l=min(m,n). Следовательно у игры (2хn) или (mx2) всегда имеется решение, содержащее не более двух активных стратегий у каждого из игроков. Если эти активные стратегии игроков будут найдены, то игра (2хn) или (mx2) превращается в игру (2х2).

Практическое решение игры (2хn) осуществляется следующим образом:

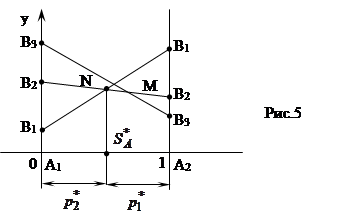
1. Строится графическое изображение игры;

2. Выделяется нижняя граница выигрыша и находится наибольшая ордината нижней границы, которая равна цене игры g;

3. Определяется пара стратегий, пересекающихся в точке оптимума. Эти стратегии являются активными стратегиями игрока В. Таким образом, игра (2хn) сведена к игре (2х2).(см. рис.5). Если в точке оптимума пересекаются более двух стратегий, то в качестве активных стратегий может быть выбрана любая пара из них. Решение игры (mx2) осуществляется

Таким образом найдена оптимальная пара стратегий 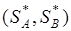, которая является решением игры (mxn) среди смешанных стратегий.

Цена игры g, которая получается при решении ЗЛП (5)-(7) и (13)-(15) должна быть одной и той же величиной. Будут ли они действительно равны? Положительный ответ на этот вопрос следует из факта, что эти две задачи образуют пару двойственных ЗЛП. Теорема о таких задачах гласит: если одна из ЗЛП двойственной пары имеет решение, то другая задача также имеет решение, причем экстремальные значения целевых функций совпадают.

Покажем, что ЗЛП (13)-(15) имеет решение. Для этого необходимо, чтоб условия (13)-(14) были совместны, т.е. имели хотя бы одно решение, а максимизируемая целевая функция была ограничена сверху.

Действительно, ограничения (13)-(14) совместны, т.к. у_j=0 ( 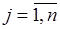) удовлетворяют ограничениям (13),(14). Следовательно, множество планов (13),(14) не пустое. В силу условия (13) все значения у_j ( 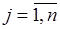) ограничены сверху, а это означает ограниченность сверху целевой функции (15). Таким образом ЗЛП (13)-(15) имеет решение. Тогда на основании теоремы о двойственности ЗЛП (5)-(7) тоже имеет решение, причем

,

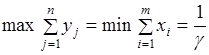т.е. в обеих задачах значение цены игры g одинаковое.

Теорема. Любая парная конечная игра с нулевой суммой имеет решение по крайней мере среди смешанных стратегий.