Проблема идентификации

Идентификация – это единственность соответствия между приведенной и структурной формами модели.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

1) идентифицируемые;

2) неидентифицируемые;

3) сверхидентифицируемые.

Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.

Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.

Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Если обозначить число эндогенных переменных в 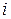-м уравнении системы через 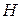, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение, — через 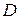, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:

Таблица 3.1

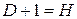
	уравнение идентифицируемо
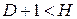
	уравнение неидентифицируемо
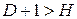
	уравнение сверхидентифицируемо

Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.

Если необходимое условие выполнено, то далее проверяется достаточное условие идентификации.

Достаточное условие идентификации. Уравнение идентифицируемо, если определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.