ВЛИЯНИЕ КУРСА КОРАБЛЯ НА АМПЛИТУДЫ

ВОЗМУЩАЮЩИХ СИЛ

При движении корабля с каким-то курсовым углом (косым курсом) по отношению к волнению корабль будет испытывать все виды качки. Мы ограничимся здесь лишь рассмотрением вертикальной, бортовой и килевой качки. Определим приближенно, как влияет курсовой угол на амплитуды возмущающих сил и моментов для этих видов качки.

Проходящая мимо корабля волна будет иметь высоту 2r₀ , но длина волны будет зависеть от курсового угла. В соответствии с рис.5.2 длину волны при расчете килевой и вертикальной качки надо определять вдоль диаметральной плоскости. Из треугольника АВС следует, что λ_ψ = λ/cos β. При расчете бор-товой качки длину волны надо брать вдоль мидельшпангоута. Из треу-гольника А₁В₁С₁ следует, что λ_θ = λ/sin β. Тогда углы волнового склона будут равны соответственно

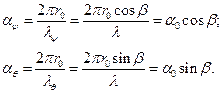(5.4)

Таким образом, в выражениях для возмущающих моментов вместо углов α₀ необходимо подставлять α _ψ и α _θ .

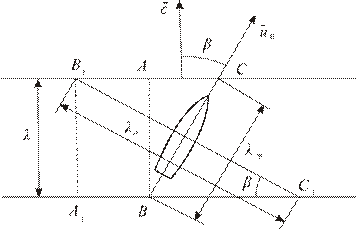
Рис. 5.2. Определение длин волн, вызывающих килевую и бортовую качку

корабля на косом волнении

Но кроме этого, меняются также поправочные коэффициенты, учитывающие конечность размеров корабля. Рассмотрим более подробно их значения для бортовой качки. Вместо коэффициента 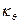необходимо использовать коэффициент 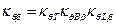, равный произведению трех коэффициентов.

Коэффициент 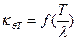, характеризует распределение давлений в волне по глубине. Это распределение не зависит от курсового угла.

Коэффициент 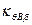определяется по формуле, выведенной ранее для коэффициента 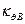, только вместо λ в нее надо подставлять λ_θ . Таким образом, .

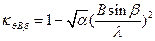Коэффициент 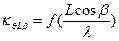учитывает влияние длины корабля на возмущающие силы. Это влияние проявляется из-за того, что в разных сечениях по длине корабля угол волнового склона имеет разное значение (см. рис.5.3, сечения 1-1, 2-2, 3-3).

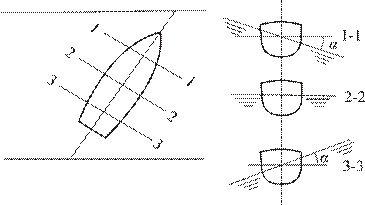
Рис. 5.3. Распределение углов волнового склона по длине корабля

на косом волнении

Определять коэффициент 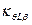можно по графику на рис. 5.4.

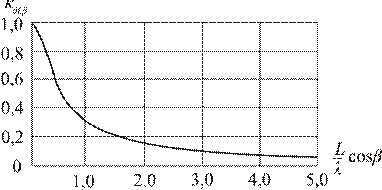
Рис. 5.4. Поправочный коэффициент, учитывающий

влияние длины корабля на амплитуды возмущающих сил при

движении его с курсовым углом к волнению