ХАРАКТЕРИСТИКИ НЕРЕГУЛЯРНОГО ВОЛНЕНИЯ
Образец записи (реализации) нерегулярного волнения изображен на рис. 2.2. Как мы видим, каждая последующая волна отличается от предыдущей по высоте и периоду, т.е. по длине. Если обозначить высоту какой-либо волны hi, амплитуда волны по определению будет равна
ri= 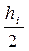 .
.
Существуют три метода описания нерегулярного волнения: статистический, спектральный и корреляционный. В практических расчетах применяются в основном статистический и спектральный методы. Рассмотрим их более подробно.
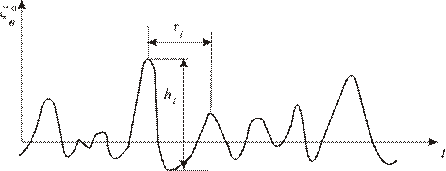
Рис. 2.2. Реализация нерегулярного волнения.
Статистический метод.
С помощью этого метода производится оценка вероятности возникновения волн различной высоты. Определить вероятность можно приближенно, взяв довольно длинную реализацию волнения и сняв с нее высоты волн. Тогда вероятность возникновения волны с амплитудой ri будет равна
pi = 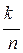 , (2.20)
, (2.20)
где k - число волн с амплитудой ri на реализации, n - общее число волн на реализации. Чем длиннее запись, тем более точно определяется вероятность.
Оценка интенсивности волнения производится с помощью дисперсии (квадрата среднего квадратичного отклонения)
Dr = 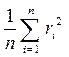 . (2.21)
. (2.21)
Средняя высота волны (в вероятностном смысле) связана с дисперсией соотношением
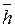 = 2,5
= 2,5 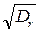 . (2.22)
. (2.22)
На практике обычно применяется не вероятность возникновения волны какой-то высоты, а обеспеченность. Обеспеченность - это вероятность возник-новения волн с высотой большей или равной заданной.
Таким образом, трехпроцентная обеспеченность обозначает, что из 100 волн только три будут иметь высоту большую или равную заданной высоте. Обеспеченность записывается в виде индекса, например, h3% , h0,5%.. Средняя высота волны имеет обеспеченность 46,5%, т.е.
h46,5% = 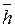 = 2,5
= 2,5 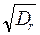 ; r46,5% =
; r46,5% = 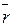 = 1,25
= 1,25 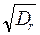 . (2.22¢)
. (2.22¢)
В таблицах балльности волн обычно выписываются значения h3%,, для которых
h3% = 5,3 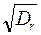 ; r3% = 2,65
; r3% = 2,65 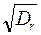 . (2.23)
. (2.23)
Иногда необходимо определить дисперсию волны, зная высоту h3%.. Из (2.23) следует
Dr = 0,143 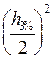 . (2.24)
. (2.24)
Высота волны 0,5% - ной обеспеченности называется максимальной
hmax = h0,5% = 6,5 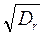 ; rmax = r0,5% = 3,25
; rmax = r0,5% = 3,25 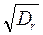 . (2.25)
. (2.25)
Обобщенная оценка интенсивности ветрового волнения производится в условных единицах - баллах. В России применяется 9 - балльная шкала (табл. 2.1). Формула Циммермана отражает связь между средними значениями h3% и l3% из этой таблицы.
Таблица 2.1. Баллы ветрового волнения
| Баллы волн | Баллы ветра | Длина волн
 , м , м
| Высота волн
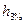 , м , м
| Период волн
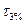 , с , с
| Словесная характеристика |
| 0-1 | отсутствует | ||||
| I | 2-3 | <5 | <0,25 | <2 | слабое |
| II | 3-4 | 5-15 | 0,25-0,75 | 2-3 | умеренное |
| III | 15-25 | 0,75-1,25 | 3-4 | значительное | |
| IV | 25-40 | 1,25-2,0 | 4-5 | значительное | |
| V | 5-6 | 40-75 | 2,0-3,5 | 5-7 | сильное |
| VI | 6-7 | 75-125 | 3,5-6,0 | 7-9 | сильное |
| VII | 7-8 | 125-170 | 6,0-8,5 | 9-11 | очень сильное |
| VIII | 8-9 | 170-220 | 8,5-11,0 | 11-12 | очень сильное |
| IX | 10-12 | >220 | >11,0 | >12 | Исключитель-ное |
Дата добавления: 2016-05-16; просмотров: 1153;
