Построение печатных соединений

Большинство алгоритмов основано на волновом алгоритме, который еще называют алгоритмом Ли.

Считаем, что монтажная схема – дерево, и хотя получение плоского изображения всегда возможно, при ограниченных размерах монтажной плоскости требуются специальные алгоритмы. Пусть задана монтажная плоскость с контактами, объединенными в подмножества (не пересекающиеся) по принадлежности к цепям. Пусть заданы запрещенные для прокладки области.

Требуется соединить контакты в каждом подмножестве, чтобы цепи не пересекались.

Разобьем плату на ячейки, например, квадраты, и будем считать их допустимыми или недопустимыми для прокладывания на данном шаге. На каждом шаге используются допустимые ячейки, число которых с каждым шагом убывает.

Допустим, на некотором шаге алгоритма необходимо соединить контакт S (исток) с контактом T (стоком). Т.е. речь пойдет о построении оптимального пути между двумя известными ячейками. Назначение истока и стока – произвольные. Считаем, что центр каждой ячейки соответствует контакту. Для каждого узла определим соседние узлы. В алгоритме Ли узлы, соседние к данному узлу – узлы, имеющие у своей ячейки общее ребро с заданным квадратом. Тогда линия связи может быть линией или ломаной с углом перегиба 90⁰.

Для соединения истока и стока применяется метод расстановки пометок, который заключается в последовательном приписывании каждому узлу пометок, состоящих из двух частей: номера узла, из которого помечен данный, и номера итерации, на которой произошло присвоение пометки.

В алгоритме Ли этот процесс называется распространением волны, а пометки множества узлов, помеченных на каждой итерации – фронтом волны. Если в этом процессе произошел прорыв , т.е. получил пометку сток Т, то это значит, что может быть установлена связь между S и T, которая на этапе проведения пути осуществляется по меткам. В противном случае пути нет.

Сначала пометку (-, 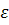(S)=0) получает исток S. Эта пометка означает, что нет узла, из которого помечается исток (-), и итерация этой пометки нулевая ( 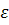(S)=0), затем помечаются все соседние к истоку узлы. Например, узлы x,y,z,u c пометками(S,ε(x)=1), (S,ε(y)=1), (S,ε(z)=1), (S,ε(u)=1) и т.д.

При этом, если некоторый узел может быть помечен из различных соседних узлов с разными пометками, то он помечается из узла с минимальным значением ε. Тогда вторая часть новой пометки должна быть равна ε+1.

Если несколько узлов имеют одинаковое минимальное ε, то берется любой из них, для пометки соседних.

Если пометился сток Т, то восстанавливается путь из Т в S, идя по пометкам (их левым частям). Правые части пометок позволяют оптимизировать выбор маршрута из истока в сток.

Таким образом, метод позволяет построить путь с минимальным числом шагов.

Пример

Соединить узлы S и T, сеть узлов N=(S,T,x₁,x₂,…,x₁₀,x₁₁).

Принцип работы алгоритма ясен из рисунка.

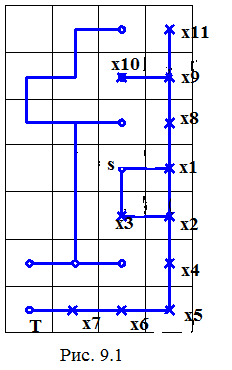S(-,ε(s)=0)

x1(s, ε(x1)=1)

x3(s, ε(x3)=1)

x2(x1, ε(x2)=2)

x4(x2, ε(x4)=3)

x5(x4, ε(x5)=4)

x6(x5, ε(x6)=5)

x7(x6, ε(x6)=6

Т(x7, ε(Т)=8)

x8(x1, ε(x8)=2)

x9(x8, ε(x9)=3)

x10(x9, ε(x10)=4)

x11(x9, ε(x11)=4)

конец, путь не найден, возвращаемся в вершину с вариантами x2 или x3.