Топологические матрицы
Задать вычислительной машине топологию цепи рисунком затруднительно, так как не существует эффективных программ распознавания образа. Поэтому топологию цепи вводят в ЭВМ в виде матриц, которые называют топологическими матрицами. Выделяют три таких матрицы: узловую матрицу, контурную матрицу и матрицу сечений.
1. Узловая матрица (матрица соединений) – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы.
Для графа на рис. 3 имеем число узлов m=4 и число ветвей n=6. Тогда запишем матрицу АН , принимая, что элемент матрицы  (i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узломi . Сориентировав ветви графа на рис. 3, получим
(i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узломi . Сориентировав ветви графа на рис. 3, получим

| ||
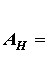
| 
| 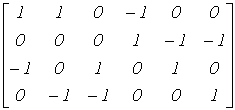
|
.Данная матрица АН записана для всех четырех узлов и называется неопределенной. Следует указать, что сумма элементов столбцов матрицы АН всегда равна нулю, так как каждый столбец содержит один элемент +1 и один элемент -1, остальные нули.
Обычно при расчетах один (любой) заземляют. Тогда приходим к узловой матрице А (редуцированной матрице), которая может быть получена из матрицы АН путем вычеркивания любой ее строки. Например, при вычеркивании строки “4” получим

| ||

| 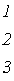
| 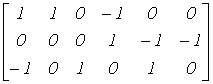
|
.Число строк матрицы А равно числу независимых уравнений для узлов 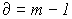 , т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа.
, т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа.
Дата добавления: 2017-02-04; просмотров: 604;
