Динамическая прифуговка ножей как метод выравнивания радиусов резания

Наряду с механическими способами установки ножей на практике находит применение особый метод выравнивания радиусов резания, получивший название динамической фуговки. Этот метод заключается в сошлифовывании с ножей части материала мелкозернистым оселком при вращении инструмента с нормальной рабочей скоростью. Суппорт с абразивным бруском (24АМ28С1К) осторожно подводят к окружности резания ножей. При появлении искр выполняют продольную подачу со скоростью 1… 2 м/мин. Поперечную подачу (0,005 мм на двойной ход) осуществляют, надвигая брусок на ножи, когда он находится за пределами вала. Фугование проводят до тех пор, пока не появятся фаски на всех ножах. Ширина фуговочной фаски не должна превышать 0,15… 0,5 мм, что требует [13] достаточно точной предварительной выставки всех ножей на один номинальный радиус резания.

Фугование ножей позволяет улучшить качество обработки за счет повышения точности сборной фрезы.

В современных учебниках по дисциплинам "Оборудование отрасли" и "Резание древесины" [13,28] указывается, что для обработки древесины со скоростью подачи свыше 20 м/мин обязательна динамическая (при вращении инструмента с нормальной рабочей скоростью) фуговка ножей с целью выравнивания их радиусов резания. Однако ни в одном из указанных источников и других работах не рассматривается вопрос взаимосвязи предельно допустимой фаски (обозначим ее буквой А) и той степенью неточности ∆, которую имела данная фреза до момента ее прифуговки.

Согласно рис.67 величина фугованной фаски для заданных параметров фрезы в первом приближении может быть найдена из треугольников ВСМ и ВСД как разность отрезков ВМ и ВД.

Конечное выражение взаимозависимости размера фугованной фаски А и исходной точности инструмента ∆ будет иметь вид

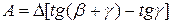, (109)

где β – угол заострения лезвия ножа, град;

γ – передний угол резания фрезы, град.

Фактический размер фаски соответствует длине дуги КL (рис.68), которая образуется в результате пересечения окружности R₂ с линиями передней и задней грани резца.

При известных значениях координат точек К и L кратчайшее расстояние между ними может быть найдено из выражения

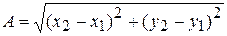, (110)

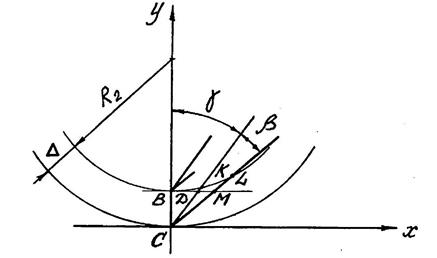
Рис. 67. Расчетная схема по определению фугованной фаски

где А – расстояние между координатами точек К и L:

x₁, y₁ – координаты точки К:

x₂, y₂ – координаты точки L.

Для нахождения координат точек К и L необходимо составить и решить соответствующие системы уравнений окружности с радиусом R₂ и прямых в плоскости передней и задней грани.

Согласно рис.7 уравнение окружности будет иметь вид

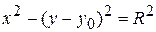, (111)

где x₀ = 0 и y₀= R + ∆ - координаты окружности.

Уравнение прямой, находящейся в плоскости передней грани

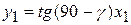, (112)

где γ – передний угол, град;

x₁ и y₁ - координаты точки К.

Уравнение прямой, находящейся в плоскости задней грани

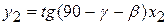, (113)

где β – угол заострения резца, град;

x₂ и y₂ – координаты точки L.

Для нахождения координат точек К и L системы уравнений будут иметь вид

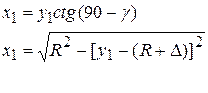
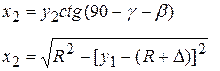
Решим задачу по определению величины фугованной фаски для конкретного случая:

Диаметр фрезы D = 200 мм;

Предварительная точность установки резцов ∆ = 0,2;

Контурные углы резания γ = 25⁰, β = 40⁰.

Координатный метод определения взаимозависимости рассматриваемых параметров позволил подтвердить корректность некоторых упрощений при решении данной задачи более простым геометрическим способом. При этом расхождения результатов расчетов не превысили 1 %.

Например для условия : γ = 30⁰; β = 40⁰; ∆ = 0,1 мм; радиус резания R = 50 мм величина фаски А по формуле 16 составила А₁ = 0,21701 мм, а по уточненным расчетам А₂ = 0,21913. Процентное расхождение оказалось всего 0,967 %

Таким образом, для ведения практических расчетов по определению величины фугованной фаски в зависимости от исходной точности инструмента вполне можно пользоваться формулой (109).