Числовые характеристики некоторых распределений
Биномиальное распределение. Это распределение рассматривалось в примере 3.2 (лекция 3). Пусть Х – распределена по биномиальному закону с параметрами n, p (n – число испытаний, p –вероятность успеха), q=1–p. Рассмотрим с.в. Хi c законом распределения 0®q, 1®p (i = 1,2, …, n). Математическое ожидание 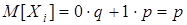 . Случайная величина
. Случайная величина 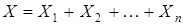 , причем с.в.
, причем с.в. 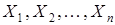 независимы и распределены одинаково. Следовательно,
независимы и распределены одинаково. Следовательно,
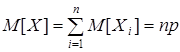 .
.
Вычислим дисперсию 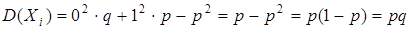 .
.
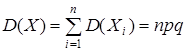 .
.
Итак,
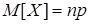 . . 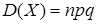
|
Распределение Пуассона. Пуассоновский закон распределение имеет вид 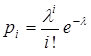 , xi = i = 0, 1, … .
, xi = i = 0, 1, … .
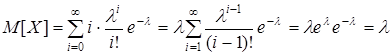 .
.

= 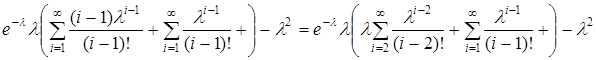 =
=
= 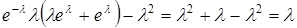 .
.
Итак,
 . . 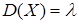 . .
|
Равномерное распределение.
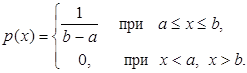
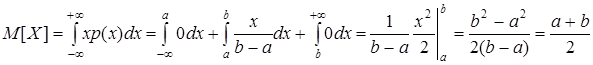 .
.
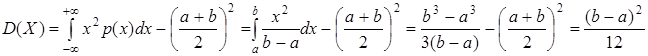 .
.
Итак,
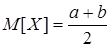 . . 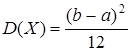 . .
|
Показательное распределение.
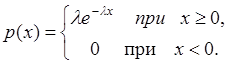
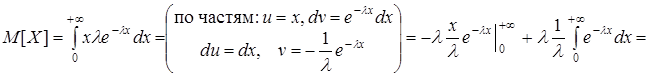
= 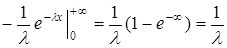 .
.
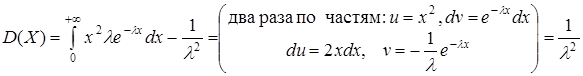 .
.
Итак,
 . . 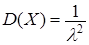 . .
|
Нормальное распределение.
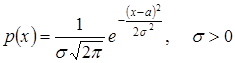
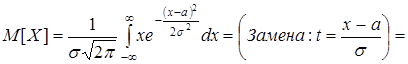
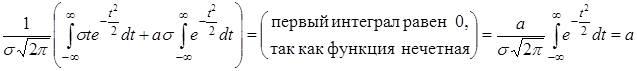 .
.
Аналогично можно вычислить дисперсию 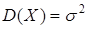 .
.
Итак,
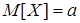 . . 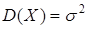 . .
|
5.2 Вероятность попадания с.в. в числовой промежуток
Пусть Х – ДСВ. Тогда 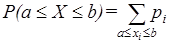 .
.
Рассмотрим НСВ Х. Так как 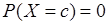 для любого числа с, то для НСВ вероятности
для любого числа с, то для НСВ вероятности 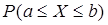 =
= 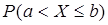 =
= 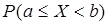 =
=  .
.
Для вычисления вероятности 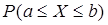 можно применить две формулы:
можно применить две формулы:
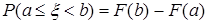 ,
,
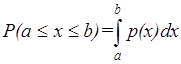 .
.
Если интеграл “берущийся”, то никаких проблем не возникает. Для нормального распределения вопрос вычисления вероятности 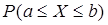 стоит особо, так как интеграл получается не “берущийся” и на практике часто приходится вычислять эту вероятность.
стоит особо, так как интеграл получается не “берущийся” и на практике часто приходится вычислять эту вероятность.
Предварительно рассмотрим функцию Лапласа, вычислению которой приводится задача вычисления вероятности 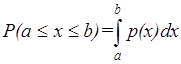 для нормального распределения.
для нормального распределения.
Функцией Лапласа называется функция
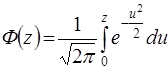 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Обзор парциальных программ | | | Виды и типы дошкольных образовательных учреждений, профессиональная деятельность специалистов ДОУ |
Дата добавления: 2017-02-04; просмотров: 1026;
